पाठ – 9
त्रिकोणमिति के कुछ अनुप्रयोग
In this post we have given the detailed notes of class 10 Math chapter 9 Some Applications of Trigonometry in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 9 त्रिकोणमिति के कुछ अनुप्रयोग के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 9 |
| Chapter Name | त्रिकोणमिति के कुछ अनुप्रयोग (Some Applications of Trigonometry) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 9 त्रिकोणमिति के कुछ अनुप्रयोग
दैनिक जीवन में त्रिकोणमिति के उपयोग
त्रिकोणमिति का वास्तविक जीवन की स्थितियों से कई समस्याओं को हल करने में व्यापक अनुप्रयोग है। लंबाई या ऊंचाई की अप्रत्यक्ष माप के लिए सबसे अच्छे तरीकों में से एक त्रिकोणमितीय ही हैं। त्रिकोणमिति का उपयोग भूगोल, खगोल विज्ञान आदि में बड़े पैमाने पर किया जाता है।
त्रिकोणमिति के ज्ञान का उपयोग मानचित्रों के निर्माण के लिए भी किया जाता है, जो अक्षांशों और अक्षांशों के संबंध में विभिन्न द्वीपों की स्थिति निर्धारित करते हैं। सीबीएसई सिलैबस में त्रिकोणमिति के केवल आधारभूत उदाहरण ही हैं। यदि आपको तिवारी अकादमी की वेबसाइट की सामग्री तक पहुंचने में कोई कठिनाई हो रही है, तो मदद के लिए हमसे संपर्क करें। हम जल्द से जल्द आपकी मदद करेंगे।
त्रिकोणमिति के प्रयोग (Use of Trigonometry)
- किसी बहुत ऊँची इमारत (building) या मीनार (tower) की ऊँचाई ज्ञात करने में
- किसी नदी/समुद्र की चौड़ाई ज्ञात करने में
- पृथ्वी से ग्रहों (planets) और तारों (stars) की दूरी ज्ञात करने में
- मानचित्र (map) बनाने और अक्षांश एवं देशांतर (latitude and longitude) के सापेक्ष किसी द्वीप (island) की स्थिति ज्ञात करने में
- किसी उड़ती चीज की किसी बिंदु से दूरी या ऊँचाई ज्ञात करने में
- इंजीनियरिंग और भौतिक विज्ञान (physics) में
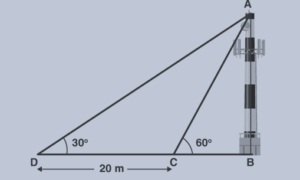
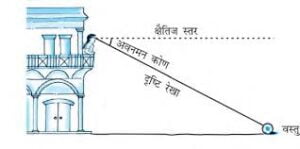
- दृष्टि रेखा (sight line) – प्रेक्षक की आँख से प्रेक्षक द्वारा देखी गई वस्तु के बिंदु को मिलाने वाली रेखा।
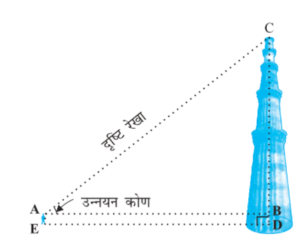
- क्षैतिज रेखा (horizontal line) – प्रेक्षक के पाद-बिंदु से प्रेक्षक द्वारा देखी गई वस्तु के पाद-बिंदु को मिलाने वाली रेखा जबकि वस्तु का पाद-बिंदु (footer point) उसी तल पर हो जिस तल पर स्वयं प्रेक्षक खड़ा है।
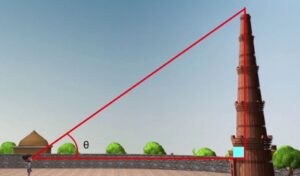
- उन्नयन कोण (elevation angle) – दृष्टि रेखा और क्षैतिज रेखा से बना कोण जबकि यह क्षैतिज स्तर से ऊपर हो।
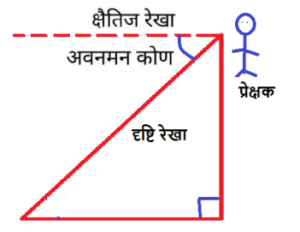
- अवनमन कोण (depression angle) – दृष्टि रेखा और क्षैतिज रेखा से बना कोण जबकि यह क्षैतिज स्तर से नीचे हो।
- जैसे-जैसे प्रेक्षक/वस्तु अन्य प्रेक्षक/वस्तु की ओर चलते जाते हैं तो उन्नयन कोण/अवनमन कोण का मान बढ़ता जाता है। इसका विलोमशः भी सत्य है।
◆ प्रश्नों हल करते समय ध्यान रखें कि पहले प्रश्न को अच्छी तरह समझ लें अन्यथा आप हमेशा अनुचित उत्तर पाएँगे।
◆ यदि प्रश्न/हल में दो समकोण बनते हैं तो ध्यान रखें कि हमें सबसे पहले ये जानना होता है कि उनमें क्या चीज उभयनिष्ठ (Common) है। यदि उस उभयनिष्ठ भुजा का मान ज्ञात नहीं है तो सबसे पहले उसे ही ज्ञात करना होता है।
◆ उचित त्रिकोणमितीय अनुपात के प्रयोग द्वारा ही प्रश्न को हल करें। जहाँ आप cot A का प्रयोग करते हैं वहाँ tan A से भी उत्तर (answer) सही मिलता है।
इसी प्रकार का सम्बन्ध अन्य त्रिकोणमितीय अनुपातों में भी होता है।
◆ अज्ञात भुजा को आप कोई भी चर (variable) मान सकते हैं परंतु यदि किसी भुजा को दो भागों में बाँटा गया है और भुजा की कुल लम्बाई ज्ञात है, तो आप एक भाग को (x)और दूसरे भाग को (कुल लम्बाई-x) मानते हैं।
◆ अवनमन कोण ज्ञात होने पर हम पहले समांतर रेखा (parallel line) और एकांतर कोण की मदद से उन्नयन कोण ज्ञात करते हैं, फिर प्रश्न को हल करते हैं।
◆ समकोण त्रिभुज की वह भुजा जिसमें त्रिभुज से बाहर अतिरिक्त रेखा हो, पहले उसे घटाकर (subtract) प्रश्न को हल करें।
Example:
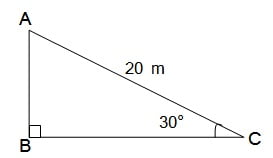
सर्कस का एक कलाकार एक 20 m लंबी डोर पर चढ़ रहा है जो अच्छी तरह से तनी हुई है और भूमि पर सीधे लगे खंभे के शिखर से बंध हुआ है। यदि भूमि स्तर के साथ डोर द्वारा बनाया गया कोण 30° का हो तो खंभे की ऊँचाई ज्ञात कीजिए (देखिए आकृति)|
Solution:
माना खंभे की ऊँचाई = h मीटर
डोरी की लंबाई = 20 मीटर
θ = 30०
समकोण त्रिभुज ABC में;

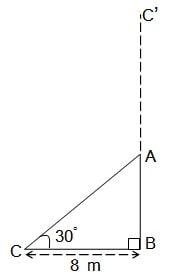
आँधी आने से एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 30० का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 8 m है। पेड़ की ऊँचाई ज्ञात कीजिए।
Solution:
माना पेड़ की ऊँचाई BC’ है और पेड़ बिंदु A से टूटकर
जमीन पर बिंदु C पर झुकी है |
θ = 30°, BC = 8 m
समकोण त्रिभुज ABC में, AB भुजा के लिए,

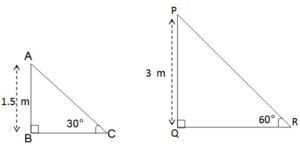
एक ठेकेदार बच्चों को खेलने के लिए एक पार्क में दो फिसलनपट्टी लगाना चाहती है। 5 वर्ष से कम उम्र के बच्चों के लिए वह एक ऐसी फिसलनपट्टी लगाना चाहती है जिसका शिखर 1.5 m की ऊँचाई पर हो और भूमि के साथ 30° के कोण पर झुका हुआ हो, जबकि इससे अधिक उम्र के बच्चों के लिए वह 3 m की ऊँचाई पर एक अधिक ढाल की फिसलनपट्टी लगाना चाहती है, जो भूमि के साथ 60° का कोण बनाती हो। प्रत्येक स्थिति में फिसलनपट्टी की लंबाई क्या होनी चाहिए?
Solution:

भूमि के एक बिंदु से, जो मीनार के पाद-बिंदु से 30 m की दूरी पर है, मीनार के शिखर का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए।
Solution:
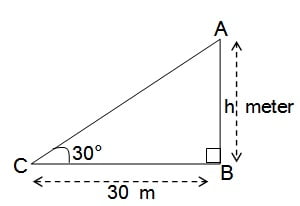
माना मीनार AB की ऊँचाई = h मीटर
बिंदु C से मीनार के पाद बिंदु B की दुरी = 30 m
समकोण ΔABC में,

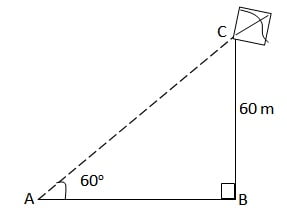
भूमि से 60 m की ऊँचाई पर एक पतंग उड़ रही है। पतंग में लगी डोरी को अस्थायी रूप से भूमि के एक बिंदु से बांध् दिया गया है। भूमि के साथ डोरी का झुकाव 60° है। यह मानकर कि डोरी में कोई ढील नहीं है, डोरी की लंबाई ज्ञात कीजिए।
Solution:

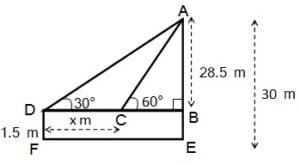
1.5 m लंबा एक लड़का 30 m ऊँचे एक भवन से कुछ दूरी पर खड़ा है। जब वह ऊँचे भवन की ओर जाता है तब उसकी आँख से भवन के शिखर का उन्नयन कोण 30° से 60° हो जाता है। बताइए कि वह भवन की ओर कितनी दूरी तक चलकर गया है।
Solution:
माना कि वह लड़का x m दूर भवन की ओर गया |
लडके ऊंचाई छोड़कर भवन की ऊंचाई (AB) = 30 m – 1.5 m
= 28.5 m
समकोण त्रिभुज ABC में,

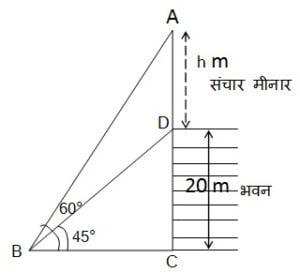
भूमि के एक बिंदु से एक 20 m ऊँचे भवन के शिखर पर लगी एक संचार मीनार के तल और शिखर के उन्नयन कोण क्रमशः 45° और 60° है। मीनार की ऊँचाई ज्ञात कीजिए।
Solution:
माना संचार मीनार की ऊंचाई (AD) = h m
भवन की ऊंचाई (DC) = 20 m
माना भूमि पर वह बिंदु B है |
भवन सहित मीनार की ऊंचाई (AC) = (20 + h) m
समकोण त्रिभुज BCD में,

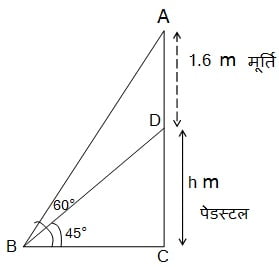
एक पेडस्टल के शिखर पर एक 1.6 m ऊँची मूर्ति लगी है। भूमि के एक बिंदु से मूर्ति के शिखर का उन्नयन कोण 60° है और उसी ¯बदु से पेडस्टल के शिखर का उन्नयन कोण 45° है। पेडस्टल की ऊँचाई ज्ञात कीजिए।
Solution:
माना पेडस्टल की ऊंचाई h मीटर है |
मूर्ति की ऊंचाई = 1.6 m
समकोण त्रिभुज BCD में,

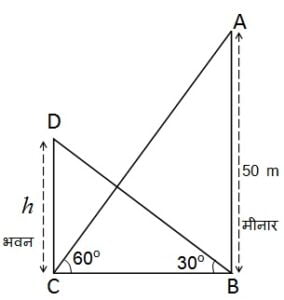
एक मीनार के पाद-बिंदु से एक भवन के शिखर का उन्नयन कोण 30o है और भवन केपाद-बिंदु से मीनार के शिखर का उन्नयन कोण 60° है। यदि मीनार 50m ऊँची हो, तो भवन की
ऊँचाई ज्ञात कीजिए।
Solution:
माना भवन की ऊंचाई = h m
समकोण त्रिभुज ABC में,

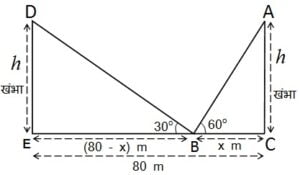
एक 80 m चैड़ी सड़क के दोनों ओर आमने-सामने समान लंबाई वाले दो खंभे लगे हुए हैं। इन दोनों खंभों के बीच सड़क के एक बिंदु से खंभों के शिखर के उन्नयन कोण क्रमशः 60° और 30° है। खंभों की ऊँचाई और खंभों से बिंदु की दूरी ज्ञात कीजिए।
Solution:
माना भूमि पर वह बिंदु B है |
और खंभों की ऊंचाई = h मीo,
B बिंदु से एक खंभे की दुरी = x m
तो दुसरे खंभे की दुरी = (80 – x) m
समकोण त्रिभुज ABC में,

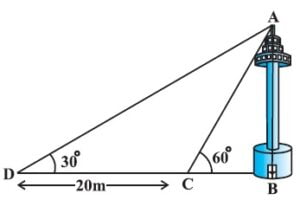
एक नहर के एक तट पर एक टीवी टॉवर उर्ध्वार्धर खड़ा है टॉवर के ठीक सामने दूसरे तट के एक अन्य बिंदु से टॉवर के शिखर का उन्नयन कोण 60° है। इसी तट पर इस बिंदु से 20 m दूर और इस बिंदु को मीनार के पाद से मिलाने वाली रेखा पर स्थित एक अन्य बिंदु से टावर के शिखर का उन्नयन कोण 30° है । टॉवर की ऊँचाई और नहर की चैड़ाई ज्ञात कीजिए।
Solution:
माना टॉवर (AB) की ऊंचाई = h मीo
नहर BC की चौड़ाई = x मीo
समकोण त्रिभुज ABC में,

7 m ऊँचे भवन के शिखर से एक केबल टावर के शिखर का उन्नयन कोण 60° है और इसके पाद का अवनमन कोण 45o है। टॉवर की ऊँचाई ज्ञात कीजिए।
Solution:
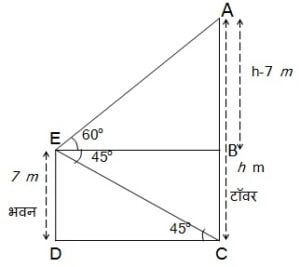
माना टॉवर की ऊँचाई = h मीटर
भवन DE की ऊंचाई = 7 मीo
DE = BC = 7 मीo
AB की लंबाई = h – 7 मीo
समकोण त्रिभुज EDC में,

समुद्र-तल से 75 m ऊँची लाइट हाउस के शिखर से देखने पर दो समुद्री जहाजों के अवनमन कोण 30° और 45° हैं। यदि लाइट हाउस के एक ही ओर एक जहाज दूसरे जहाज के ठीक पीछे हो तो दो जहाजों के बीच की दूरी ज्ञात कीजिए।
Solution:
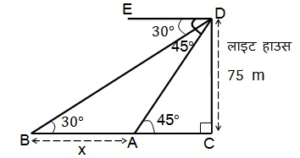
माना दो जहाजों A तथा B है
जिनका अवनमन कोण क्रमश: 45° और 30° है |
लाइट-हाउस DC की ऊंचाई = 75 m
चूँकि अवनमन कोण उन्नयन कोण के बराबर होता है |
∴ ∠DAC = 45o और ∠DBC = 30o

1.2 m लंबी एक लड़की भूमि से 88.2 m की ऊँचाई पर एक क्षैतिज रेखा में हवा में उड़ रहे गुब्बारे को देखती है। किसी भी क्षण लड़की की आँख से गुब्बारे का उन्नयन कोण 60° है। कुछ समय बाद उन्नयन कोण घटकर 30° हो जाता है | इस अन्तराल के दौरान गुब्बारे द्वारा तय की गयी दुरी ज्ञात कीजिए |
Solution:
लड़की की ऊंचाई = 1.2 m
भूमि से गुब्बारे की ऊंचाई = 88.2 m
लड़की को छोड़कर गुब्बारे की ऊंचाई = 88.2 – 1.2
AB = DE = 87.0 m
तय दुरी = BE
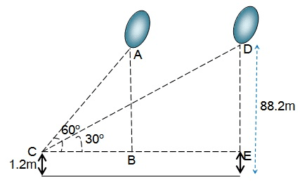
समकोण DABC में,

अर्थात इस अन्तराल के दौरान गुब्बारे द्वारा तय की गयी दुरी 87√3 m है |
एक सीध राजमार्ग एक मीनार के पाद तक जाता है। मीनार के शिखर पर खड़ा एक आदमी एक कार को 30° के अवनमन कोण पर देखता है जो कि मीनार के पाद की ओर एक समान चाल से जाता है। छः सेकंड बाद कार का अवनमन कोण 60° हो गया। इस बिंदु से मीनार के पाद तक पहुँचने में कार द्वारा लिया गया समय ज्ञात कीजिए।
Solution: माना कार को बिंदु C से मीनार के पाद B तक पहुँचने में x सेकेण्ड लगता है |
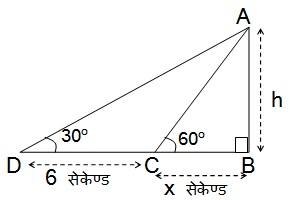

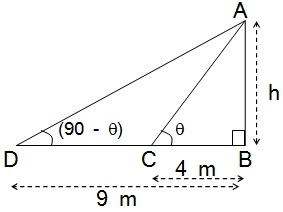
मीनार के आधर से और एक सरल रेखा में 4 m और 9 m की दूरी पर स्थित दो ¯बदुओं से मीनार के शिखर के उन्नयन कोण पूरक कोण हैं। सिद्ध कीजिए कि मीनार की ऊँचाई 6 m है।
Solution:
माना मीनार की ऊँचाई = h मीटर है |
समकोण त्रिभुज ABC में,

We hope that class 10 Math Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग (Some Applications of Trigonometry) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग (Some Applications of Trigonometry) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…