पाठ – 9
समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
In this post we have given the detailed notes of class 9 Math chapter 9 Areas of Parallelograms and Triangles in Hindi. These notes are useful for the students who are going to appear in class 9 board exams.
इस पोस्ट में कक्षा 9 के गणित के पाठ 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 9 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Math |
| Chapter no. | Chapter 9 |
| Chapter Name | समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Areas of Parallelograms and Triangles) |
| Category | Class 9 Math Notes in Hindi |
| Medium | Hindi |
पाठ 9, समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
संगत तलीय क्षेत्र
एक सरल बंद आकृति द्वारा तल का घेरा हुआ भाग उस आकृति का संगत तलीय क्षेत्र कहलाता है। इस तलीय क्षेत्र का परिमाण या माप उस आकृति का क्षेत्रफल कहलाता है। इस परिमाण या माप को सदैव एक संख्या (किसी मात्रक में), की सहायता से व्यक्त किया जाता है।
दूसरे शब्दों में किसी आकृति का क्षेत्रफल (किसी मात्रक में) एक संख्या है जो उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (जुड़ी) होती है।
- यदि A और B दो सर्वांगसम आकृतियाँ हैं, तो क्षेत्रफल (A) = क्षेत्रफल (B) है तथा
- यदि एक आकृति T द्वारा निर्मित क्षेत्र दो आकृतियों P और फ़ द्वारा निर्मित अनातिव्यापी तलीय क्षेत्रें से मिल कर बना है, तो क्षेत्रफल (T) = क्षेत्रफल (P) + क्षेत्रफल (Q) होगा।
उभयनिष्ठ आधार पर बनी आकृतियाँ
दो आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित कही जाती हैं, यदि उनका एक उभयनिष्ठ आधार (भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (या का शीर्ष) उस आधार के समांतर किसी रेखा पर स्थित हों।
सर्वांगसम आकृतियाँ
‘दो आकृतियाँ सर्वांगसम कही जाती हैं, यदि उनके आकार और माप समान हों।’ दूसरे शब्दों में, यदि दो आकृतियाँ A और B सर्वांगसम हों, तो आप एक अक्स कागज का प्रयोग करके, एक आकृति को दूसरी आकृति पर इस प्रकार रख सकते हैं कि एक आकृति दूसरी को पूरा-पूरा ढक ले। अतः, यदि दो आकृतियाँ A और B सर्वांगसम हैं, तो उनके क्षेत्रफल अवश्य ही बराबर (समान) होने चाहिए।
परन्तु इस कथन का विलोम सत्य नहीं है। दूसरे शब्दों में, बराबर क्षेत्रफलों वाली दो आकृतियों का सर्वांगसम होना आवश्यक नहीं है।
स्मरणीय तथ्य
- एक आकृति का क्षेत्रफल उस आकृति द्वारा घेरे गए तल के भाग से संबद्ध (किसी मात्रक में) एक संख्या होती है।
- दो सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं, परन्तु इसका विलोम आवश्यक रूप से सत्य नहीं है।
- यदि एक आकृति T द्वारा निर्मित कोई तलीय क्षेत्र किन्हीं दो आकृतियों P और Q द्वारा निर्मित दो अनातिव्यापी तलीय क्षेत्रें से मिल कर बना है, तो क्षेत्रफल (T) = क्षेत्रफल (P) + क्षेत्रफल (Q) है, जहाँ क्षेत्रफल (X) आकृति X का क्षेत्रफल व्यक्त करता है।
एक ही आधार और एक ही समांतर रेखाओं के बीच समांतर चतुर्भुज
एक ही आधार और एक ही समांतर रेखाओं के बीच बने समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
उदाहरण
दो समांतर चतुर्भुज ABCD और EE’CD हैं, जो एक ही आधार DC और एक ही समांतर रेखाओं AE′ और DC के बीच स्थित हैं।
चूँकि ∆ ADE ≅ ∆ A′D′E′
अतः क्षेत्रफल (ADE) = क्षेत्रफल (A′D′E′)
साथ ही क्षेत्रफल (ABCD) = क्षेत्रफल (ADE) + क्षेत्रफल (EBCD)
= क्षेत्रफल (A′D′E′) + क्षेत्रफल (EBCD)
= क्षेत्रफल (EE′CD)
अतः, दोनों समांतर चतुर्भुज क्षेत्रफल में बराबर हैं।
प्रमेय 9.1:
एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
उपपत्ति
दो समांतर चतुर्भुज ABCD और EFCD दिए हुए हैं, जो एक ही आधार DC और एक ही समांतर रेखाओं AF और DC के बीच स्थित हैं।
हमें क्षेत्रफल (ABCD) = क्षेत्रफल (EFCD) सिद्ध करना है।
∆ ADE और ∆ BCF में
∠DAE = ∠CBF (AD ∥ BC और तिर्यक रेखा AF से संगत कोण) (1)
∠AED = ∠BFC (ED ∥ FC और तिर्यक रेखा AF से संगत कोण) (2)
इसलिए, ∠ADE = ∠BCF (त्रिभुज का कोण योग गुण) (3)
साथ ही, AD = BC (समांतर चतुर्भुज की सम्मुख भुजाएँ) (4)
अतः ∆ ADE ≅ ∆ BCF (ASA नियम तथा (1), (3) तथा (4) द्वारा)
इसलिए, क्षेत्रफल ADE = क्षेत्रफल BCF (सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं) (5)
अब, क्षेत्रफल (ABCD) = क्षेत्रफल (ADE) + क्षेत्रफल (EDCB)
= क्षेत्रफल (BCF) + क्षेत्रफल (EDCB) [(5) से ]
= क्षेत्रफल (EFCD)
अतः, समांतर चतुर्भुज ABCD और EFCD क्षेत्रफल में बराबर हैं।
नोट
एक ही आधार या बराबर आधारों और एक ही समांतर रेखाओं के बीच बने समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
उपरोक्त कथन का विलोम इस प्रकार है:
एक ही आधार (या बराबर आधारों) और बराबर क्षेत्रफलों वाले समांतर चतुर्भुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज
दो त्रिभुज ABC और PBC ऐसे देखेंगे जो एक ही आधार BC और एक ही समांतर रेखाओं BC और AP के बीच स्थित हैं। ऐसे दोनों त्रिभुजों के क्षेत्रफल (लगभग) बराबर हैं। इसको इस प्रकार से सिद्ध किया जा सकता है:
रेखा AP को आगे बढ़ाते हैं तथा बिंदु C से रेखा AP पर दो रेखाएं AB और BP के समान्तर खींचते हैं जो क्रमशः D और R पर मिलती हैं।
इस प्रकार CD ∥ BA और CR ∥ BP
यहाँ पर हमें दो समान्तर चतुर्भुज PBCR और ABCD प्राप्त होते हैं। ये दोनों चतुर्भुज एक ही आधार BC और एक ही समान्तर रेखाओं BC और AR के बीच स्थित हैं।
अतः, क्षेत्रफल ((ABCD) = क्षेत्रफल (PBCR)
अब, ∆ ABC ≅ ∆ CDA और ∆ PBC ≅ ∆ CRP
अतः क्षेत्रफल (ABC) = ![]() क्षेत्रफल (ABCD)
क्षेत्रफल (ABCD)
और क्षेत्रफल (PBC) = ![]() क्षेत्रफल (PBCR)
क्षेत्रफल (PBCR)
इसलिए, क्षेत्रफल (ABC) = क्षेत्रफल (PBC)
प्रमेय 9.2
एक ही आधार (या बराबर आधारों ) और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।
अब, मान लीजिए ABCD एक समांतर चतुर्भुज है जिसका एक विकर्ण AC है। मान लें कि AN ⊥ DC है। ध्यान दीजिए कि
∆ ADC ≅ ∆ CBA है
अतः, क्षेत्रफल (ADC) = क्षेत्रफल (CBA)
इसलिए, क्षेत्रफल (ADC) = ![]() क्षेत्रफल (ABCD)
क्षेत्रफल (ABCD)
= ![]() (DC × AN)
(DC × AN)
अतः ∆ ADC का क्षेत्रफल = ![]() (आधार DC) × संगत शीर्षलम्ब AN
(आधार DC) × संगत शीर्षलम्ब AN
दूसरे शब्दों में, किसी त्रिभुज का क्षेत्रफल उसके आधार (एक भुजा) और संगत शीर्षलम्ब (या ऊँचाई) के गुणनफल के आधे के बराबर होता है।
स्मरणीय तथ्य
- दो आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित कही जाती हैं, यदि उनमें एक उभयनिष्ठ आधार (एक भुजा) हो तथा उभयनिष्ठ आधार के सम्मुख प्रत्येक आकृति के शीर्ष (का शीर्ष) उस आधार के समांतर किसी रेखा पर स्थित हों।
- एक ही आधार (या बराबर आधारों) वाले और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज क्षेत्रफल में बराबर होते हैं।
- समांतर चतुर्भुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब का गुणनफल होता है।
एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
उपरोक्त प्रमेय का प्रयोग निम्नलिखित उदाहरण में करते हैं:
उदाहरण:
दर्शाइए कि त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
हल
मान लीजिए ABC एक त्रिभुज है और AD उसकी एक माध्यिका है। आप यह दर्शाना चाहते हैं कि
क्षेत्रफल (ABD) = क्षेत्रफल (ACD)
चूँकि त्रिभुज के क्षेत्रफल में शीर्षलम्ब सम्बद्ध होता है, इसलिए आइए AN ⊥ BC खींचें।
अब, क्षेत्रफल (ABD) = ![]() × आधार × शीर्षलम्ब (∆ ABD का)
× आधार × शीर्षलम्ब (∆ ABD का)
= ![]() BD × AN
BD × AN
= ![]() CD × AN (चूँकि BD = CD)
CD × AN (चूँकि BD = CD)
= ![]() × आधार × शीर्षलम्ब (∆ ACD का)
× आधार × शीर्षलम्ब (∆ ACD का)
= क्षेत्रफल (ACD)
स्मरणीय तथ्य
- एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले समांतर चतुर्भुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
- यदि एक त्रिभुज और एक समांतर चतुर्भुज एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हों, तो त्रिभुज का क्षेत्रफल समांतर चतुर्भुज के क्षेत्रफल का आधा होता है।
- एक ही आधार (या बराबर आधारों) वाले और एक ही समांतर रेखाओं के बीच स्थित त्रिभुज क्षेत्रफल में बराबर होते हैं।
- त्रिभुज का क्षेत्रफल उसके आधार और संगत शीर्षलम्ब के गुणनफल का आधा होता है।
- एक ही आधार (या बराबर आधारों) वाले और बराबर क्षेत्रफलों वाले त्रिभुज एक ही समांतर रेखाओं के बीच स्थित होते हैं।
- त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है।
उद्देश्य
- एक ही आधार पर तथा एक ही समांतर रेखाओं के बीच की आकृतियाँ बनाना।
- एक ही आधार पर तथा एक ही समांतर रेखाओं के बीच के समांतर चतुर्भुजों को समझना।
- एक ही आधार पर तथा एक ही समांतर रेखाओं के बीच के त्रिभुजों को समझना।
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल से सम्बंधित प्रमेयों को सिद्ध करना।
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल से सम्बंधित उदाहरणों को हल करना।
परिभाषाएँ
समतल क्षेत्र के विस्तार अथवा उसकी माप को उस क्षेत्र का क्षेत्रफल कहते हैं। किसी समतल का वह भाग जो किसी बंद आकृति के अंदर हो, वह उसी आकृति का समतल क्षेत्र कहलाता है। दो सर्वांगसम आकृतियों के क्षेत्रफल सामान होते हैं, लेकिन सामान क्षेत्रफल वाली आकृतियाँ सर्वांगसम हों यह आवश्यक नहीं है। किसी आकृति के क्षेत्रफल को AR से भी दर्शाया जा सकता है। उदाहरण के लिए ‘त्रिभुज ABC का क्षेत्रफल’ के स्थान पर ar(ABC) भी लिखा जा सकता है।
एक ही आधार पर बनी आकृतियाँ
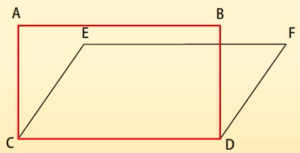
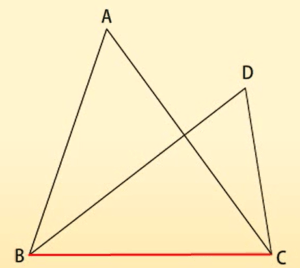
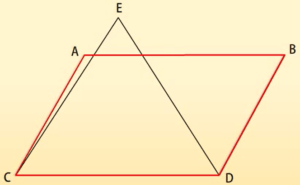
एक आधार और एक ही समांतर रेखाओं के बीच की आकृतियाँ
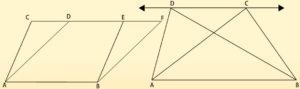
परिणामः दो आकृतियाँ यदि एक ही आधार पर स्थित हों और उभयनिष्ठ आधार के सम्मुख स्थित उनके शीर्ष एक ऐसी रेखा पर स्थित हो जो उस आधार के समांतर हो। तो वो आकृतियाँ एक ही आधार और एक ही समांतर रेखाओं के बीच की आकृतियाँ कहलाएंगी।
एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज
प्रमेयः एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भजों के क्षेत्रफल सामान होते हैं।
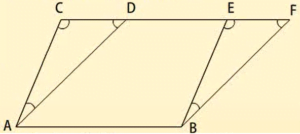
दिया हैं: दो समांतर चतुर्भुज ABEC और ABFD, दिए गए हैं, जो एक ही / आधार AB तथा एक समांतर रेखाओं AB और CF के बीच स्थित हैं।
सिद्ध करेः
क्षेत्रफल (ABEC) = क्षेत्रफल (ABED)
![]() ADC और
ADC और ![]() BEF में,
BEF में,
![]() ACD =
ACD = ![]() BEF …….. (1)
BEF …….. (1)
(समांतर रेखाओं AC || BE तथा तिर्यक रेखा CF के संगत कोण हैं।)
![]() ADC =
ADC = ![]() BFE …….. (2)
BFE …….. (2)
(समांतर रेखाओं AD || BF तथा तिर्यक रेखा CF के संगत कोण हैं।)
इसलिए, ![]() CAD =
CAD = ![]() EBF …….. (3)
EBF …….. (3)
(त्रिभुज के कोण योग गुण के अनुसार)
साथ ही, AC = BE …….. (4)
(समांतर चतुर्भुज ABEC की सम्मुख भुजाएं)
इसलिए, ![]() ADC
ADC ![]()
![]() BEF
BEF
[ASA नियम द्वारा समीकरण (1), (3), (4), का प्रयोग करते हुए।]
क्षेत्रफल (ADC) = क्षेत्रफल (BEF) …….. (5)
(सर्वांगसम आकृतियों के क्षेत्रफल सामान होते हैं)
अब, ABEC का क्षेत्रफल = (ADC) का क्षेत्रफल + (ABEC) का क्षेत्रफल
अब हम जानते हैं कि, ADC = BEF
इसलिए हम इसे इस तरह भी लिख सकते हैं,
(ABEC) का क्षेत्रफल = (BEF) का क्षेत्रफल + (EDAB) का क्षेत्रफल (समीकरण 5 से)
= ABFD का क्षेत्रफल
इसलिए, समांतर चतुर्भुज ABEC तथा ABED दोनों के क्षेत्रफल बराबर हैं।
प्रमेय का विलोम
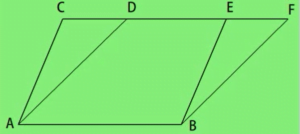
एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित समांतर चतुर्भुज के क्षेत्रफल सामान होते हैं।
एक ही आधार पर स्थित सामान क्षेत्रफल वाले समांतर चतुर्भुज एक ही समांतर रेखाओं की बीच स्थित होते हैं।
उदाहरण: यदि एक समांतर चतुर्भुज और एक त्रिभुज एक ही आधार और एक ही समांतर रेखाओं के बीच स्थित हैं तो सिद्ध कीजिये कि समांतर चतुर्भुज उसी त्रिभुज जैसे दो त्रिभुजों से बना होता है।
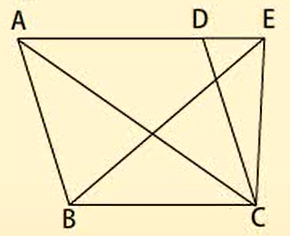
मान लेते हैं कि एक उभयनिष्ठ आधार BC पर, और एक ही समांतर रेखाओं AE और BC के बीच समांतर चतुर्भुज ABCD और एक त्रिभुज EBC स्थित हैं, अब । सिद्ध करते हैं कि समांतर चतुर्भुज ABCD त्रिभुज EBC जैसे दो त्रिभुजों से बना है।
रचनाः रेखा AC खींचिए।
समांतर चतुर्भुज ABCD = 2![]() ABC (विकर्ण AC, समांतर चतुर्भुज को बाँट रही है।)
ABC (विकर्ण AC, समांतर चतुर्भुज को बाँट रही है।)
किन्तु ![]() ABC =
ABC = ![]() EBC,
EBC,
(एक ही आधार BC और एक ही समांतर रेखाओं AE और BC के बीच स्थित हैं)
समांतर चतुर्भुज ABCD = 2![]() EBC
EBC
इति सिद्धम
उदाहरणः एक समलम्ब ABCD, जिसमें AB || DC के विकर्ण AC और BD एक दूसरे को 0 पर काटते हैं। सिद्ध करिये कि ![]() AOD का क्षेत्रफल =
AOD का क्षेत्रफल = ![]() BOC का क्षेत्रफल।
BOC का क्षेत्रफल।
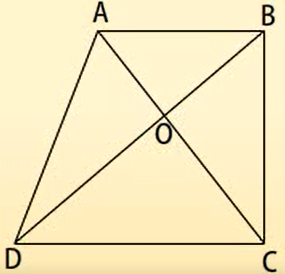
हल:
यह देखा जा सकता है कि ADAC और ADBC एक ही आधार DC पर और एक ही समांतर रेखाओं AB और CD के बीच स्थित हैं।
![]() (
(![]() DAC) का क्षेत्रफल = (
DAC) का क्षेत्रफल = (![]() DBC) का क्षेत्रफल
DBC) का क्षेत्रफल
![]() (
(![]() DAC) का क्षेत्रफल – (
DAC) का क्षेत्रफल – (![]() DOC) का क्षेत्रफल = (
DOC) का क्षेत्रफल = (![]() DBC) का क्षेत्रफल – (
DBC) का क्षेत्रफल – (![]() DOC) का क्षेत्रफल
DOC) का क्षेत्रफल
= (![]() AOD) का क्षेत्रफल = (
AOD) का क्षेत्रफल = (![]() BOC) का क्षेत्रफल।
BOC) का क्षेत्रफल।
एक ही आधार तथा एक ही समांतर रेखाओं के बीच स्थित त्रिभुज
प्रमेयः एक ही आधार (या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित त्रिभुजों के क्षेत्रफल सामान होते हैं।
दिया गया है: एक ही आधार BC और एक ही समांतर रेखाओं BC तथा AD के बीच स्थित दो त्रिभुज ABC और DBCI
– एक ही आधार तथा एक ही समांतर रेखाओं के बीच
स्थित त्रिभुज
प्रमेयः एक ही आधार (या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित त्रिभुजों के क्षेत्रफल सामान होते हैं। दिया गया है: एक ही आधार BC और एक ही समांतर रेखाओं BC तथा AD के बीच स्थित दो त्रिभुज ABC और DBCT सिद्ध करना है: (AABC) का क्षेत्रफल = (ADBC) का क्षेत्रफल
Areas of Parallelograms and Triangles
BL
एक ही आधार तथा एक ही समांतर रेखाओं के बीच
स्थित त्रिभुज
_
—
_
_
_
A
Er- – – – –
F
रचनाः B से होते हुए, CA के समांतर, E पर बनी DA को काटती हुई, BE खींचिए और C से होते हुए, BD के समांतर, F पर बनी ।। AD को काटती हुई, CF खींचिए। उपपत्तिः हमारे पास दो समांतर रेखाएं BE और CA हैं। (निर्माण के अनुसार) BCII EA (दिया है।) इसलिए, चतुर्भुज BCAE एक समांतर चतुर्भुज है। ठीक इसी तरह, BCFD भी एक समांतर चतुर्भुज है। अब, समांतर चतुर्भुज BCAE तथा समांतर चतुर्भुज BCFD एक ही आधार BC तथा एक ही समांतर रेखाओं BC तथा AD के बीच स्थित हैं। इसलिए, समांतर चतुर्भुज BCAE का क्षेत्रफल = समांतर चतुर्भुज BCFD का क्षेत्रफला …………….(1) हम जानते हैं कि समांतर चतुर्भुजों के विकर्ण उन्हें बराबर क्षेत्रफल वाले दो त्रिभुजों में बाँट देते हैं।
एक ही आधार तथा एक ही समांतर रेखाओं के बीच
स्थित त्रिभुज
इसलिए, क्षेत्रफल (ADBC) = क्षेत्रफल ( समांतर चतुर्भुज BCFD) … …2) और क्षेत्रफल (AABC) = क्षेत्रफल ( समांतर चतुर्भुज BCAE) ………….(3)
Er- – – – – – – – – – -A
–
–
–
–
–
–
–
–
–
चूंकि, समांतर चतुर्भुज BCAE का क्षेत्रफल = समांतर’ चतुर्भुज BCFD का क्षेत्रफला (समीकरण 1 से)
+ (समांतर चतुर्भुज
BCFD) का क्षेत्रफल
= = (समांतर चतुर्भुज
BCAE) का क्षेत्रफल
इसलिए, क्षेत्रफल (AABC) = क्षेत्रफल (ADBC)
समान क्षेत्रफल वाले दो त्रिभुज, जिनके आधार एक ही हैं (या बराबर हैं), एक ही समांतर रेखाओं के बीच स्थित होते हैं।
उदाहरण
उदाहरणः
एक त्रिभुज ABC, में, E माध्यिका AD का मध्य बिंदु है। सिद्ध करिये कि (BED) का क्षेत्रफल = 1 ABC का क्षेत्रफल का
हलः
दिया है:
AD, AABC की माध्यिका है। इसलिए यह त्रिभुज ABC को बराबर क्षेत्रफल वाले दो त्रिभुजों में बाँट देगी। :: AABD का क्षेत्रफल = AACD का क्षेत्रफल = AABD का क्षेत्रफल = 7 AABC का क्षेत्रफ. .(1)
त्रिभुज ABD में AD का Eमध्य बिंदु है।
उदाहरण
इसलिए, BE माध्यिका है।
:: (ABED) का क्षेत्रफल = (AABE) का क्षेत्रफल
= ABED का क्षेत्रफल == AABE का क्षेत्रफल = ABED का क्षेत्रफल = 1 का क्षेत्रफल (AABC) (समीकरण समीकरण (1) के अनुसार = जिससे यह सिद्ध होता है कि BED का क्षेत्रफल = 1 ABC के क्षेत्रफल का
,
उदाहरण
उदाहरण: सिद्ध करिये कि किसी समांतर चतुर्भुज के विकर्ण उसे बराबर क्षेत्रफल वाले चार त्रिभुजों में विभाजित कर देते हैं।
हलः
हम जानते हैं कि समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं। इसलिए 0, AC और BD का मध्य बिंदु है। AABC में BO माध्यिका है। इसलिए, यह इसे बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करेगी। :: (AAOB) का क्षेत्रफल = (ABOC) का क्षेत्रफल ………….(1) त्रिभुज BCD में CO माध्यिका है।
::: (ABOC) का क्षेत्रफल = (ACOD) का क्षेत्रफल …… … (2) LACOD) का क्षेत्रफल = (AAOD) का क्षेत्रफल ……………..(3)
00:20:22
00:03:39
समीकरण (1), (2),और (3), से हमें पता चलता है कि
(AAOB) का क्षेत्रफल = (ABOC) का क्षेत्रफल = (ACOD) का क्षेत्रफल = (AAOD) का क्षेत्रफल इसलिए, यह सिद्ध हुआ कि, किसी समांतर चतुर्भुज के विकर्ण उसे बराबर क्षेत्रफल वाले चार त्रिभुजों में विभाजित कर देते हैं।
क्या आप जानते हैं ।
सिकंदरिया के हीरोन (एक शताब्दी ई.पू.) में त्रिभुज के क्षेत्रफल के सूत्र की खोज की थी।।। गणित के इतिहास में वह सबसे अधिक इसी सूत्र के कारण जाने जाते हैं, जिसका नाम उन्ही के नाम पर है।
सारांश
आइये हमने जो कुछ सीखा है, उसे संक्षेप में दोहराएं।
८) किसी आकृति का क्षेत्रफल वह संख्या (किसी इकाई में) है, जो उस आकृति के अंदर आने वाले
समतल को दर्शाती है। ८) दो सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं। लेकिन इस कथन का विलोम भी सही हो
यह आवश्यक नहीं है। 5) दो आकृतियाँ यदि एक ही आधार पर स्थित हैं और उभयनिष्ठ आधार के सम्मुख स्थित उनके शीर्ष
एक ऐसी रेखा पर स्थित हैं जो आधार के समांतर है तो वो आकृतियाँ एक ही आधार और एक
ही समांतर रेखाओं के बीच की आकृतियाँ कहलाएंगी। ८) एक ही आधार (या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित समांतर
चतुर्भुजों के क्षेत्रफल बराबर होते हैं। ८) एक ही आधार (या बराबर आधारों) पर स्थित समान क्षेत्रफल वाले समांतर चतुर्भुज एक ही समांतर
रेखाओं के बीच स्थित होते हैं।
k
सारांश
आइये हमने जो कुछ सीखा है, उसे संक्षेप में दोहराएं। ।
1) एक ही आधार (या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित त्रिभुजों के
क्षेत्रफल सामान होते हैं।
सारांश
आइये हमने जो कुछ सीखा है, उसे संक्षेप में दोहराएं।
८) किसी आकृति का क्षेत्रफल वह संख्या (किसी इकाई में) है, जो उस आकृति के अंदर आने वाले
समतल को दर्शाती है। ८) दो सर्वांगसम आकृतियों के क्षेत्रफल बराबर होते हैं। लेकिन इस कथन का विलोम भी सही हो
यह आवश्यक नहीं है। 5) दो आकृतियाँ यदि एक ही आधार पर स्थित हैं और उभयनिष्ठ आधार के सम्मुख स्थित उनके शीर्ष
एक ऐसी रेखा पर स्थित हैं जो आधार के समांतर है तो वो आकृतियाँ एक ही आधार और एक
ही समांतर रेखाओं के बीच की आकृतियाँ कहलाएंगी। ८) एक ही आधार (या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित समांतर
चतुर्भुजों के क्षेत्रफल बराबर होते हैं। ८) एक ही आधार (या बराबर आधारों) पर स्थित समान क्षेत्रफल वाले समांतर चतुर्भुज एक ही समांतर
रेखाओं के बीच स्थित होते हैं।
सारांश
आइये हमने जो कुछ सीखा है, उसे संक्षेप में दोहराएं।।
८) एक ही आधार (या बराबर आधारों) और एक ही समांतर रेखाओं के बीच स्थित त्रिभुजों के
क्षेत्रफल सामान होते हैं। ८) किसी त्रिभुज का क्षेत्रफल उसके आधार और लम्ब के गुणनफल का आधा होता है। ८) एक ही आधार (या बराबर आधारों) पर स्थित समान क्षेत्रफल वाले त्रिभुज एक ही समांतर
रेखाओं के बीच स्थित होते हैं। ८) एक त्रिभुज की माध्यिका उसे बराबर क्षेत्रफल वाले दो त्रिभुजों में बांटती है। एक ही आधार ___(या बराबर आधारों) पर स्थित समान क्षेत्रफल वाले समांतर चतुर्भुज एक ही समांतर रेखाओं
के बीच स्थित होते हैं। ) एक त्रिभुज की मध्य उसे दो बराबर क्षेत्रफल वाले त्रिभुज में बांटती है।
We hope that class 9 Math Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Areas of Parallelograms and Triangles) Notes in Hindi helped you. If you have any queries about class 9 Math Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल (Areas of Parallelograms and Triangles) Notes in Hindi or about any other Notes of class 9 Math in Hindi, so you can comment below. We will reach you as soon as possible…