पाठ – 10
वृत
In this post we have given the detailed notes of class 10 Math chapter 10 Circles in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 10 वृत के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 10 |
| Chapter Name | वृत (Circles) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 10, वृत
वृत्त
किसी एक निश्चित बिंदु से समान दूरी पर स्थित बिंदुओं का बिन्दुपथ वृत्त कहलाता है। यह निश्चित बिंदु, वृत्त का केंद्र कहलाता है, केंद्र और वृत्त की परिधि के किसी भी बिन्दु के बीच की दूरी वृत्त की त्रिज्या कहलाती है। वृत्त एक साधारण बंद वक्र होता है जो समतल को दो क्षेत्रों में विभाजित करता है: एक आंतरिक और एक बाहरी।
वृत्त एक प्रकार का शांकव (शंकु परिच्छेद) होता है जिसकी उत्केंद्रता (Eccentricity) शून्य होती है अर्थात नियता (Directrix) समतल में अनंत पर स्थित होती है। एक वृत्त को एक विशेष प्रकार के दीर्घवृत्त के रूप में भी परिभाषित किया जा सकता है जिसमें दोनों नाभियाँ (Focii) संपाती होती हैं और उत्केन्द्रता 0 होती है। यूक्लिड के अनुसार, ‘वृत्त एक रेखा से घिरा हुआ एकविमीय समतल होता है और किसी निश्चित बिंदु से लेकर उस बंधरेखा तक खींची गई सभी रेखाएं बराबर होती हैं। इस बंधरेखा को परिधि और इस निश्चित बिंदु को वृत्त का केंद्र कहते हैं।’

वृत्त और त्रिज्या
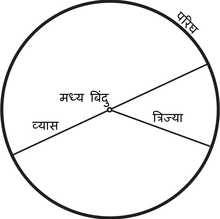
वृत्त: वृत्त एक तल के उन बिदुओं का समूह होता है जो एक नियत बिदु (केंद्र) से अचर दूरी (त्रिज्या) पर होते हैं।
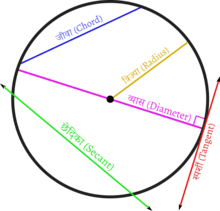
त्रिज्या: त्रिज्या या अर्धव्यास किसी वृत्त के केन्द्र से उसकी परिधि तक की दूरी को कहते हैं।
चाप (Arc): वृत्त की परिधि का कोई भी भाग।
केंद्र (Centre): वृत्त पर स्थित सभी बिंदुओं से समदूरस्थ बिंदु।
जीवा (Chord): एक रेखाखंड, जो वृत्त पर स्थित किन्हीं दो बिन्दुओं को मिलने पर बनता है। एक जीवा वृत्त को दो वृत्तखंडों में विभाजित करती है।

परिधि (Circumfrence): वृत्त के चारों ओर की वक्र लंबाई।
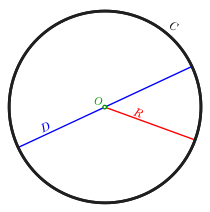
व्यास (Diameter): एक रेखाखंड जिसके अंतबिन्दु वृत्त पर स्थित होते हैं और जो केंद्र से गुजरता है या वृत्त के किन्हीं दो बिंदुओं के बीच की अधिकतम दूरी है। यह वृत्त की सबसे बड़ी जीवा होती है और यह त्रिज्या की दोगुनी होती है।
डिस्क (Disc): एक वृत्त से घिरा अन्तः समतलीय क्षेत्र।
त्रिज्या (Radius): वृत्त के केंद्र से वृत्त की परिधि के किसी भी बिंदु तक का एक रेखाखंड, जो व्यास का आधा होता है।

चाप (Arc), त्रिज्यखंड (Sector) एवं वृत्तखंड (Segment)
त्रिज्यखंड (Sector): किन्हीं दो त्रिज्याओं के बीच एक चाप से घिरा क्षेत्र।
वृत्तखण्ड (Segment): केंद्ररहित एक क्षेत्र जो वृत्त की एक जीवा और एक चाप से घिरा होता है। एक जीवा वृत्त को दो वृत्तखंडों में विभाजित करती है।
छेदन रेखा या छेदिका (Secant): एक विस्तारित जीवा, जो वृत्त के समतलीय होती है तथा वृत्त को दो बिन्दुओं पर प्रतिच्छेदित करती है।
स्पर्शी या स्पर्श रेखा (Tangent): वृत्त के समतलीय सीधी रेखा जो एक बिंदु पर वृत्त को स्पर्श करती है।

अर्धवृत्त (Semicircle): वृत्त के व्यास तथा व्यास के अंतबिन्दुओं से बने चाप के मध्य का क्षेत्र अर्धवृत्त होता है। अर्धवृत्त का क्षेत्रफल, वृत्त के सम्पूर्ण क्षेत्रफल का आधा होता है।
वृत्त की स्पर्श रेखा
रेखा जो एक वृत्त को केवल और केवल एक ही बिन्दु पर प्रतिच्छेद करती है, वृत्त की स्पर्श रेखा कहलाती है। अर्थात वृत की स्पर्श रेखा उसे केवल एक बिन्दु पर प्रतिच्छेद करती है। स्पर्श रेखा जहाँ पर वृत्त को स्पर्श करती है उस बिंदु को स्पर्श बिंदु कहते हैं।
नोट: वृत्त के एक बिदु पर एक और केवल एक स्पर्श रेखा होती है।
वत्त की स्पर्श रेखा के गुण

- वृत्त के एक बिन्दु पर एक और केवल एक स्पर्श रेखा होती है।
- किसी वृत्त की स्पर्श रेखा छेदक रेखा की एक विशिष्ट दशा है जब संगत जीवा के दोनों सिरे संपाती हो जाएँ।
- स्पर्श रेखा और वृत्त के कॉमन प्वांट (उभनिष्ठ बिन्दु) को स्पर्श बिन्दु (point of contact) कहते हैं। तथा स्पर्श रेखा को वृत के उभयनिष्ठ बिन्दु पर स्पर्श करना कहते हैं।
- वृत्त के अंदर स्थित किसी बिन्दु से जाने वाली वृत्त पर कोई स्पर्श रेखा नहीं है।
- वृत्त पर स्थित किसी बिन्दु से वृत्त पर एक और केवल एक स्पर्श रेखा है।
- वृत्त के बाहर स्थित किसी बिन्दु से जाने वाली वृत्त पर दो और केवल दो स्पर्श रेखाएँ हैं।
- बाह्य बिन्दु P से वृत के स्पर्श बिन्दु तक स्पर्श रेखा खंड की लम्बाई को बिन्दु P से वृत्त पर स्पर्श रेखा की लम्बाई कहते हैं।
छेदक रेखा तथा वृत्त का केंद्र
छेदक रेखा: एक वृत्त को दो बिंदुओं में प्रतिच्छेद करने वाली रेखा को छेदक कहा जाता है।
वृत्त का केंद्र: वृत्त के मध्य वह बिंदु, जिससे परिधि हमेशा समान दूरी पर होता है, वृत्त का केन्द्र कहलाता है।
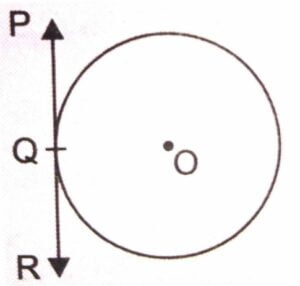
वृत्त के किसी बिदु पर स्पर्श रेखा स्पर्श बिदु से जाने वाली त्रिज्या पर लंब होती है।
हमें केंद्र O वाला एक वृत्त दिया है और एक बिदु P पर स्पर्श रेखा XY दी है। हमें सिद्ध करना है कि OP, XY पर लंब है।
XY पर P के अतिरिक्त एक बिदु Q लीजिए और OQ को मिलाइए।
बिदु Q वृत्त के बाहर होना चाहिए (क्यों?)
ध्यान दीजिए कि यदि Q वृत्त के अंदर है तो XY वृत्त की एक छेदक रेखा हो जाएगी और वह वृत्त की स्पर्श रेखा नहीं होगी)।
अतः, OQ त्रिज्या OP से बड़ी है।
अर्थात् OQ > OP
क्योंकि यह बिदु P के अतिरिक्त XY के प्रत्येक बिदु के लिए सत्य है, OP बिदु O से XY के अन्य बिदुओं की न्यूनतम दूरी है। इसलिए OP, XY पर लंब है।
टिप्पणी:
- उपर्युक्त प्रमेय से हम यह भी निष्कर्ष निकाल सकते हैं कि वृत्त के किसी बिदु पर एक और केवल एक स्पर्श रेखा होती है।
- स्पर्श बिदु से त्रिज्या को समाहित करने वाली रेखा को वृत्त के उस बिदु पर ‘अभिलंब’ भी कहते हैं।
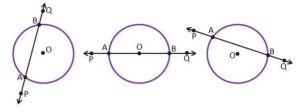
एक बिंदु से एक वृत्त पर स्पर्श रेखाओं की संख्या
किसी बाहरी बिंदु से वृत्त पर केवल दो स्पर्श रेखाएँ खींची जा सकती हैं।
वाह्य बिंदु से वृत्त पर खींची गई स्पर्श रेखाओं की लंबाइयाँ बराबर होती है।
उपपत्ति:
हमें केंद्र O वाला एक वृत्त, वृत्त के बाहर का एक बिंदु P तथा P से वृत्त पर दो स्पर्श रेखाएँ PQ, PR दी है।
हमें सिद्ध करना है कि PQ = PR
इसके लिए हम OP, OQ और OR को मिलाते हैं। तब ∠ OQP तथा ∠ ORP समकोण हैं क्योंकि ये त्रिज्याओं और स्पर्श रेखाओं के बीच के कोण हैं और प्रमेय 10.1 से ये समकोण है।
अब समकोण त्रिभुजों OQP तथा ORP में,
OQ = OR (एक ही वृत्त की त्रिज्याएँ)
OP = OP (उभयनिष्ठ)
अतः ∆ OQP / ∆ ORP (RHS सर्वांगसमता द्वारा)
इससे प्राप्त होता है PQ = PR (CPCT)
टिप्पणी:
- प्रमेय को पाइथागोरस प्रमेय का प्रयोग करके भी निम्न प्रकार से सिद्ध किया जा सकता हैः PQ² = OP² – OQ² = OP² – OR² = PR² (क्योंकि OQ = OR) जिससे प्राप्त होता है कि PQ = PR
- यह भी ध्यान दीजिए कि ∠OPQ = ∠OPR, अतः OP कोण QPR का अर्धक है, अर्थात् वृत्त का केंद्र स्पर्श रेखाओं के बीच के कोण अर्धक पर स्थित होता है।
- सिद्ध कीजिए कि दो सकेंद्रीय वृत्तों में बड़े वृत्त की जीवा जो छोटे वृत्त को स्पर्श करती है, स्पर्श बिदु पर समद्विभाजित होती है।
हमें केंद्र O वाले दो सकेंद्रीय वृत्त C₁ और C₂ तथा बड़े वृत्त C₁ की जीवा AB, जो छोटे वृत्त C₂ को बिदु P पर स्पर्श करती है, दिए हैं।
हमें सिद्ध करना है कि AP = BP
आइए OP को मिलाएँ। इस प्रकार AB, C₂ के बिदु P पर स्पर्श रेखा है और OP त्रिज्या है।
अतः प्रमेय 10.1 से
OP ⊥ AB
अब AB वृत्त C₁ की एक जीवा है और OP ⊥ AB है। अतः, OP जीवा AB को समद्विभाजित करेगी क्योंकि केंद्र से जीवा पर खींचा गया लंब उसे समद्विभाजित करता है,
अर्थात् AP = BP
स्मरणीय तथ्य
किसी वृत्त पर बाह्य बिंदु से केवल दो स्पेश रेखाएं खींची जा सकती है।
वृत्त की स्पर्श रेखा स्पर्श बिदु से जाने वाली त्रिज्या पर लंब होती है।
बाह्य बिदु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लंबाइयाँ समान होती हैं।
वृत्त (Circle) – उन सभी बिंदुओं का समूह जो एक स्थिर बिंदु (केंद्र) बराबर दुरी (त्रिज्या) पर होते हैं, वृत्त कहलाता है।
अप्रतिच्छेदी रेखा (non-intersecting lines or parallel lines) – जब दी गई रेखा और वृत्त का कोई बिंदु उभयनिष्ठ (common) न हो, तो वह रेखा अप्रतिच्छेदी रेखा कहलाती है।
छेदक रेखा (penetrative lines) – जब दी गई रेखा और वृत्त के दो बिंदु उभयनिष्ठ हो, तो वह रेखा छेदक रेखा कहलाती है।
स्पर्श रेखा (tangent line) – जब दी गई रेखा और वृत्त का केवल एक बिंदु उभयनिष्ठ हो, तो वह रेखा स्पर्श रेखा कहलाती है।
स्पर्श बिंदु (touch point) – दी गई रेखा और वृत्त के एकमात्र उभयनिष्ठ बिंदु को स्पर्श बिंदु कहते हैं।
- वृत्त के स्पर्श बिंदु पर केवल एक ही रेखा सम्भव है।
- वृत्त की किसी छेदक रेखा के समांतर केवल दो स्पर्श रेखाएँ होती हैं।
- वृत्त की स्पर्श रेखा छेदक रेखा की वह विशेष स्थिति है जब संगत जीवा के दोनों सिरे संपाती (coincidence) हो जाते हैं।
वृत्त की स्पर्श रेखा वृत्त की उस त्रिज्या (radius) पर लंब होती है, जो स्पर्श बिंदु से खींची गई हो।
- एक बिंदु और एक वृत्त दिए होने पर निम्न में से कोई एक स्थिति सम्भव है : –
- स्थिति I – वृत्त के अंदर स्थित बिंदु से वृत्त पर कोई स्पर्श रेखा नहीं खींची जा सकती।
- स्थिति II – वृत्त पर स्थित किसी बिंदु से केवल एक स्पर्श रेखा खींची जा सकती है।
- स्थिति III – वृत्त के बाहर स्थित बिंदु से वृत्त पर दो स्पर्श रेखाएँ खींची जा सकती हैं।
- स्पर्श रेखा की लंबाई (length of tangent line) – वृत्त के बाहर स्थित बिंदु से स्पर्श बिंदु तक की दूरी स्पर्श रेखा की लंबाई कहलाती है।
- वृत्त के किसी बाह्य बिंदु (exterior point) से खींची गई स्पर्श रेखाएँ बराबर होती हैं।
- केंद्र से वृत्त की जीवा (chord) पर खींचा गया लंब (perpendicular) जीवा को समद्विभाजित (bisect) करता है।
- दो सकेंद्रीय वृत्तों (concentric circles) में यदि बड़े वृत्त की जीवा छोटे वृत्त की स्पर्श रेखा है, तो जीवा स्पर्श बिंदु पर समद्विभाजित (bisect) होगी।
- वृत्त के बाहर स्थित किसी बिंदु से दो स्पर्श रेखाएँ खींचकर और और स्पर्श बिंदुओं को मिलाने पर एक समद्विबाहु त्रिभुज (isosceles triangle) बनता है और स्पर्श बिंदुओं पर बने कोण बराबर होते हैं।
Example:
सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती है |
हल :
दिया है : O केंद्र वाले वृत्त की दो स्पर्श रेखाएँ AB तथा CD हैं जो वृत्त को X तथा Y पर क्रमश: स्पर्श करती है |
सिद्ध करना है : AB || CD
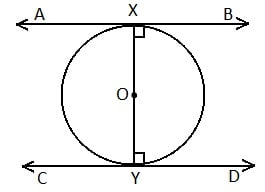
प्रमाण :
OX ⊥ AB (स्पर्श बिंदु को केंद्र से मिलाने वाली रेखा स्पर्श बिंदु पर लंब होती है )
अत: ∠BXO = 90० …….. (i)
इसीप्रकार, OY ⊥ CD
अत: ∠DYO = 90० …….. (i)
समीकरण (i) तथा (ii) जोड़ने पर
∠BXO + ∠DYO = 90० + 90०
∠BXO + ∠DYO = 180०
चूँकि एक ही ओर से अंत:आसन्न कोण संपूरक हैं, इसलिए
AB || CD Proved
एक बिन्दु A से जो एक वृत्त के केंद्र से 5cm दूरी पर है, वृत्त पर स्पर्श रेखा की लंबाई 4cm है | वृत्त की त्रिज्या ज्ञात कीजिए |
हल : बिंदु A से केंद्र की दुरी (OA) = 5 cm
स्पर्श रेखा AB की लंबाई = 4 cm
वृत्त की त्रिज्या OB = ?
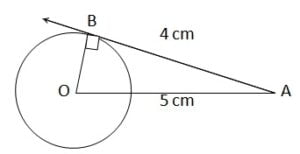
समकोण त्रिभुज AOB में, पैथागोरस प्रमेय से
OA2 = OB2 + AB2
52 = OB2 + 42
52 – 42 = OB2
25 – 16 = OB2
OB2 = 9
दो सकेंद्रिय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm है | बड़े वृत्त की उस जीवा की लंबाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो|
हल :
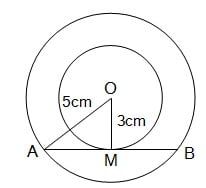
दो संकेंद्री वृत्त जिसका केंद्र O है और बड़े वृत्त की जीवा AB है जो छोटे वृत्त को बिंदु M पर प्रतिच्छेद करती है |
त्रिज्याएँ क्रमश: AO = 5 cm और OM = 3 cm है |
OM ⊥ AB है | (चूँकि जीवा को केंद्र से मिलाने वाली रेखाखण्ड जीवा पर लंब होती है |)
अत: समकोण त्रिभुज AOM में, पाइथागोरस प्रमेय से,
OA2 = OM2 + AM2
52 = 32 + AM2
52 – 32 = AM2
25 – 9 = AM2
AM2 = 16
AM = = 4 cm
अत: AB = 2 × AM
= 2 × 4 = 8 cm
जीवा की लंबाई 8 cm है |
एक वृत्त के परिगत एक चतुर्भज ABCD खींचा गया है (देखिए आकृति 10.12 ) | सिद्ध कीजिए : AB + CD = AD + BC
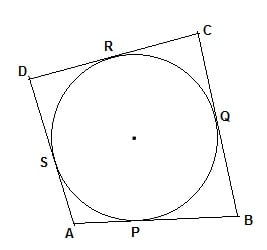
हल :
दिया है : ABCD एक O केंद्र वाले वृत्त के परिगत बना चतुर्भुज है | रेखाएँ AB, BC, CD और AD क्रमश: बिंदु P, Q, R और S पर स्पर्श करती हैं |
सिद्ध करना है : AB + CD = AD + BC
प्रमाण : P और S स्पर्श बिंदु हैं |
अत: AP = AS …………… (i) प्रमेय 10.2 से
(बाह्य बिंदु से खिंची गई स्पर्श रेखाएँ समान लंबाई की होती है |)
इसीप्रकार,
BP = BQ …………… (ii)
CR = CQ …………… (iii)
और DR = DS …………… (iv)
समी० (i), (ii), (iii) और (iv) जोड़ने पर
AP + BP + CR + DR = AS + DS + BQ + CQ
AB + CD = AD + BC Proved
आकृति 10.13 में XY तथा X’Y’, O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है | सिद्ध कीजिए की ∠AOB = 90o है |
हल :
दिया है : XY तथा X’Y’, O केंद्र वाले किसी वृत्त पर दो समांतर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है |
सिद्ध करना है : ∠AOB = 90o
प्रमाण :
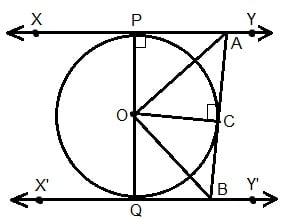
DAOP और DAOC में
PA = CA (भुजा) प्रमेय 10.2 से
∠APO = ∠ACO 90० प्रत्येक
AO = AO उभयनिष्ठ कर्ण
RHS सर्वांगसमता नियम से
DAOP @ DAOC
इसलिए, ∠PAO = ∠CAO (i) BY CPCT
इसीप्रकार DBOQ @ DBOC
इसलिए, ∠QBO = ∠CBO (ii) BY CPCT
अब XY || X’Y’ दिया है |
इसलिए, ∠PAC + ∠QBC = 180० (तिर्यक रेखा के एक ही ओर के अंत:कोणों का योग )
या (∠PAO + ∠CAO) + (∠QBO + ∠CBO) = 180०
या (∠CAO + ∠CAO) + (∠CBO + ∠CBO) = 180० (समी० (i) तथा (ii) के प्रयोग से )
या 2 ∠CAO + 2 ∠CBO = 180०
या 2 (∠CAO + ∠CBO) = 180०
या ∠CAO + ∠CBO = 90० ………….. (iii)
अब त्रिभुज AOB में,
∠AOB + ∠CAO + ∠CBO = 180०
∠AOB + 90० = 180०
∠AOB = 180० – 90०
∠AOB = 90० Proved
सिद्ध कीजिए कि किसी बाह्य बिन्दु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखंड द्वारा केंद्र पर अंतरित कोण का संपूरक होता है |
हल : दिया है : O केंद्र वाले वृत्त की की बाह्य बिंदु P से खिंची गई स्पर्श रेखाओं AP तथा BP है |
सिद्ध करना है : ∠AOB + ∠APB = 180०
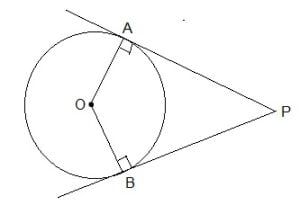
प्रमाण :
OA ⊥ AP और OB ⊥ BP (चूँकि स्पर्श रेखा से केंद्र को मिलाने वाली रेखाखंड लंब होती है |)
अत: ∠OAP = 90=……….. (i)
और ∠OBP = 90० ……….. (ii)
चूँकि APBO एक चतुर्भुज है इसलिए,
∠OAP + ∠AOB + ∠OBP + ∠APB = 360०
=> 90० + ∠AOB + 90० + ∠APB = 360०
=> 180० + ∠AOB + ∠APB = 360०
=> ∠AOB + ∠APB = 360० – 180०
=> ∠AOB + ∠APB = 180० Proved
सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज समचतुर्भुज होता है |
हल :
दिया है : ABCD एक O केंद्र वाले वृत्त के परिगत बना समांतर चतुर्भुज है | रेखाएँ AB, BC, CD और AD क्रमश: बिंदु P, Q, R और S पर स्पर्श करती हैं |
सिद्ध करना है : ABCD एक समचतुर्भुज है |
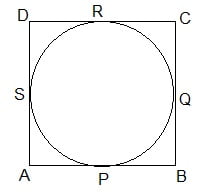
प्रमाण : चूँकि ABCD एक समांतर चतुर्भुज है इसलिए
AB = CD ………… (i) (समांतर चतुर्भुज की सम्मुख भुजा)
इसीप्रकार, BC = AD ……… (ii)
अब, P और S स्पर्श बिंदु हैं |
अत: AP = AS …………… (iii) प्रमेय 10.2 से
(बाह्य बिंदु से खिंची गई स्पर्श रेखाएँ समान लंबाई की होती है |)
इसीप्रकार,
BP = BQ …………… (iv)
CR = CQ …………… (v)
और DR = DS …………… (vi)
समी० (iii), (iv), (v) और (vi) जोड़ने पर
AP + BP + CR + DR = AS + DS + BQ + CQ
या AB + CD = AD + BC
या AB + AB = AD + AD समी० (i) तथा (ii) से
या 2 AB = 2 AD
या AB = AD ……… (vii)
समीकरण (i), (ii) और (vii) से
AB = BC = CD = AD
अत: ABCD एक समचतुर्भुज है | Proved
सिद्ध कीजिए की वृत्त के परिगत बनी चतुर्भुज की आमने – सामने की भुजाएँ केंद्र पर संपूरक कोण अंतरित करती हैं |
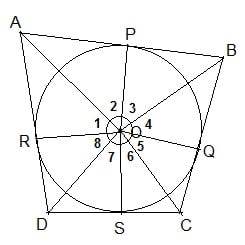
हल : दिया है : ABCD O केंद्र वाले एक वृत्त के परिगत बना चतुर्भुज है |

We hope that class 10 Math Chapter 10 वृत (Circles) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 10 वृत (Circles) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…