पाठ – 11
रचनाएँ
In this post we have given the detailed notes of class 10 Math chapter 11 Constructions in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 11 रचनाएँ के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 11 |
| Chapter Name | रचनाएँ (Constructions) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 11 रचनाएँ
रचनाएं
ज्यामितीय आकृतियों के निर्माण तथा उनसे सम्बन्धित नियमों का अध्ययन इस अध्याय के अंतर्गत विस्तार से समझाया गया है।
रेखाखंड का विभाजन
मान लीजिए कि एक रेखाखंड दिया है और आपको उसे एक दिए गए अनुपात, माना 3 : 2 में विभाजित करना है। आप इसकी लंबाई माप कर तथा दिए गए अनुपात के अनुसार एक बिंदु चिह्नित कर सकते हैं। परंतु यदि आपके पास इसे सही-सही मापने की कोई विधि न हो, तो आप इस बिंदु को कैसे प्राप्त करेंगे? इस प्रकार के बिंदु को प्राप्त करने के लिए, कई विधियाँ हैं।
एक रेखाखंड AB दिया है, हम इसको m : n के अनुपात में विभाजित करना चाहते हैं। प्रक्रिया को समझने में सहायता करने के लिए, हम m = 3 और n = 2 लेंगे।
रचना के चरणः
- AB से न्यूनकोण बनाती कोई किरण AX खींचिए।
- AX पर 5 (= m + n) बिंदु A₁, A₂, A₃, A₄ और A₅ इस प्रकार अंकित कीजिए कि AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ हो।
- BA₅ को मिलाइए।
- बिंदु A₃ (m = 3) से होकर जाने वाली A₅B के समांतर एक रेखा (A₃ पर ∠ AA₅B के बराबर कोण बनाकर) AB को एक बिंदु C पर प्रतिच्छेद करती हुई खींचिए।
तब, AC : CB = 3 : 2 है।
यह विधि कैसे हमें अभीष्ट विभाजन देती है।
क्योंकि A₃C, A₅B के समांतर है,
अतः AA₃/A₃A₅ = AC/CB (आधारभूत समानुपातिकता प्रमेय द्वारा)
रचना से, AA₃/A₃A = 3/2 है।
इससे यह निष्कर्ष निकलता है कि बिंदु C, AB को 3 : 2 अनुपात में विभाजित करता है।
एक दिए गए त्रिभुज ABC के समरूप एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की 5/3 हों (अर्थात् स्केल गुणक 5/3 है)।
एक त्रिभुज ABC दिया गया है। हमें एक त्रिभुज की रचना करनी है, जिसकी भुजाएँ ∆ ABC की संगत भुजाओं की 5/3 हों।
रचना के चरणः
- BC से शीर्ष A के दूसरी ओर न्यूनकोण बनाती हुई एक किरण BX खींचिए।
- 5 (5/3 में 5 और 3 में से बड़ी संख्या) बिंदु B₁, B₂, B₃, B₄ और B₅, BX पर इस प्रकार अंकित कीजिए कि BB₁ = B₁B₂ = B₂B₃ = B₃ = B₄B₅ हो।
- B₃ (तीसरा बिंदु, 5/3 में 5 और 3 में से छोटी संख्या) को C से मिलाइए और B₅ से होकर जाने वाली B₃C के समांतर एक रेखा, बढ़ाए गए रेखाखंड BC को C’ पर प्रतिच्छेद करती हुई खींचिए।
- C’ से होकर जाने वाली CA के समांतर एक रेखा, बढ़ाने पर रेखाखंड BA को A’ पर प्रतिच्छेद करती हुई खींचिए।
तब, A’BC’ अभीष्ट त्रिभुज है।
रचना के औचित्य सिद्ध करने के लिए, ध्यान दीजिए
∆ ABC ~ ∆ A’BC’ (कोण कोण कोण नियम से)
इसलिए, AB/A’B = AC/A’C’ = BC/BC’ है।
परंतु BC/BC’ = BB₃/BB₅ = 3/5 है।
इसलिए, BC’/BC = 5/3 है और इसीलिए A’B/AB = A’C’/AC = BC’/BC = 5/3 है।
किसी वृत्त पर स्पर्श रेखाओं की रचना
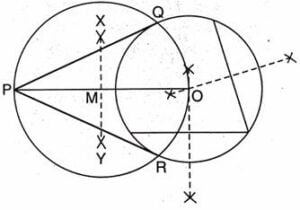
यदि कोई बिंदु वृत्त के अंदर स्थित है, तो इस बिंदु से जाने वाली वृत्त की कोई स्पर्श रेखा नहीं हो सकती है। परंतु यदि बिंदु वृत्त पर स्थित है, तो उस बिंदु पर वृत्त की एक और केवल एक स्पर्श रेखा होती है, जो उस बिंदु से जाने वाली त्रिज्या पर लंब होती है। अतः यदि आप वृत्त के किसी बिंदु पर स्पर्श रेखा खींचना चाहते हैं, तो केवल उस बिंदु से जाने वाली त्रिज्या खींचिए और उसी बिंदु पर इसकी लंब रेखा खींचिए। तब, यही अभीष्ट स्पर्श रेखा होगी। आपने यह भी देखा है कि यदि बिंदु वृत्त के बाहर स्थित है, तो इस बिंदु से वृत्त पर दो स्पर्श रेखाएँ होती हैं।
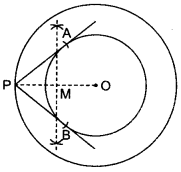
- हमें एक वृत्त जिसका केंद्र O है तथा इसके बाहर एक बिंदु P दिए हुए हैं। हमें P से वृत्त पर दोनों स्पर्श रेखाएँ खींचनी हैं।
रचना के चरण
- PO को मिलाइए और इसे समद्विभाजित करिए।
माना PO का मध्य बिंदु M है।
- M को केंद्र मान कर तथा MO त्रिज्या लेकर एक वृत्त खींचिए। माना यह दिए गए वृत्त को Q और R पर प्रतिच्छेद करता है।
- P को Q तथा R से मिलाइये।
तब, PQ और PR अभीष्ट दो स्पर्श रेखाएँ है।
आइए अब देखें कि इस रचना से हमें स्पर्श रेखाएँ किस प्रकार मिलती हैं। OQ को मिलाइए।
तब, ∠PQO अर्धवृत्त में बना एक कोण है और इसीलिए ∠PQO = 90⁰ है।
यहाँ हम कह सकते हैं कि PQ ⊥ OQ है,
क्योंकि, OQ दिए वृत्त की त्रिज्या है, इसलिए PQ वृत्त की स्पर्श रेखा ही होगी। इसी प्रकार, PR भी वृत्त की स्पर्श रेखा है।
ध्यान देने योग्य बातें
यदि वृत्त का केंद्र नहीं दिया है, तो आप कोई दो असमांतर जीवाएँ लेकर तथा उनके लंब समद्विभाजकों के प्रतिच्छेद बिंदु के रूप में केंद्र ज्ञात कर सकते हैं। इसके बाद, आप उपर्युक्त रूप से आगे बढ़ सकते हैं।
किसी रेखाखंड (line segment) को दिए गए अनुपात(2:5) में विभाजित करना : –
- पहले दी गई रेखा (AB) से न्यूनकोण (acute angle) बनाती हुई एक रेखा (AX) खींचो जिसकी लम्बाई दोनों अनुपातों के योग(2 + 5 = 7)के बराबर होनी चाहिए।
- खींची गई रेखा(AX) पर दोनों अनुपातों के योग (7) के बराबर बिंदु अंकित करो(A1, A2, A3, A4, A5, A6, A7) समान दूरियों पर (equidistant)।
- खींची गई रेखा के अंतिम बिंदु (A7) को दी गई रेखा के बिंदु (B) से मिलाकर एक अन्य रेखा (BA7) खींचो।
- दिए गए अनुपात (ratio) में से पहले अनुपात (2 = A2) से अन्य रेखा (BA7) के समांतर (parallel) एक रेखा खींचो और दी गई रेखा(AB) पर कोई बिंदु(C) अंकित करो।
- दी गई रेखा अभीष्ट अनुपात में विभाजित हो गई है। (AB:BC = 2:5)
किसी रेखाखंड को दिए गए अनुपात (2:5) में विभाजित करना (वैकल्पिक विधि द्वारा)
- दिए गए रेखाखंड (AB) से न्यूनकोण (<BAX) बनाती हुई एक रेखा (AX) और दूसरा न्यूनकोण (<ABY) बनाती हुई अन्य रेखा (BY) खींचो।
- पहले रेखाखंड (AX) पर पहले अनुपात (2) के बराबर, समान दूरियों पर बिंदु (A1, A2) अंकित करो।
- दूसरे रेखाखंड (BY) पर दूसरे अनुपात (5) के बराबर, समान दूरियों पर बिंदु (B1, B2, B3, B4, B5) अंकित करो।
- पहले रेखाखंड (AX) और दूसरे रेखाखंड (BY) के अंतिम बिंदुओं (A2 और B5) को मिलाओ।
- रेखाखंड (A2B5) और दिए गए रेखाखंड (AB) के प्रतिच्छेद बिंदु (intersecting point) को (C) अंकित करो।
- दी गई रेखा अभीष्ट अनुपात में विभाजित हो गई है। (AB:BC = 2:5)
स्केल गुणक (scale factor) – दिए गए त्रिभुज और जिस त्रिभुज की रचना की जानी है उसकी भुजाओं (sides) के अनुपात को स्केल गुणक कहते हैं।
स्केल गुणक (2/3) के अनुसार दिए गए त्रिभुज (ABC) के समरूप (similar) त्रिभुज की रचना करना : –
- दिए गए त्रिभुज के आधार (base) (BC) से शीर्ष (vertice) (A) के दूसरी ओर न्यूनकोण बनाती हुई एक किरण (ray) (BX) खींचो।
- किरण (BX) पर 3 बिंदु (2/3 में 3 बड़ा है) समान दूरियों पर अंकित करो B1, B2, B3
- किरण के अंतिम बिंदु (B3) को आधार (BC) से मिलाकर रेखा (B3C) खींचो फिर रेखा (B3C) के समांतर बिंदु (B2) से (2/3 में 2 छोटा) एक रेखा (B2C’) खींचो।
- बिंदु (C’) से रेखा (CA) के समांतर एक रेखा (C’A’) खींचो।
- ∆ A’BC’ ~ ∆ ABC
वृत्त (circle) के बाहर स्थित किसी बिंदु (L) से वृत्त पर स्पर्श रेखाओं (tangent line) की रचना करना : –
- दिए गए बिंदु (L) को वृत्त के केंद्र (O) से मिलाओ और OL को समद्विभाजित (bisect) करो।
- OL के मध्य बिंदु (midpoint) (S) को केंद्र (center) और OS को त्रिज्या (radius) मानकर एक अन्य वृत्त की रचना (construction) करो और प्रतिच्छेद बिंदुओं के नाम लिखो (P और Q)
- दिए गए बिंदु (L) को बिंदुओं (P और Q) से मिलाओ।
- LP और LQ अभीष्ट स्पर्श रेखाएँ हैं।
Example:
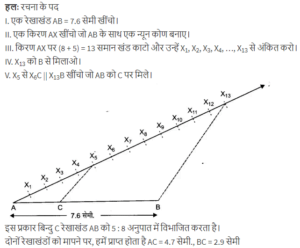
7.6 cm लंबा एक रेखाखंड खींचिए और इसे 5: 8 अनुपात में विभाजित कीजिए | दोनों को मापिए

4cm, 5cm और 6cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 2/3 गुनी हों |
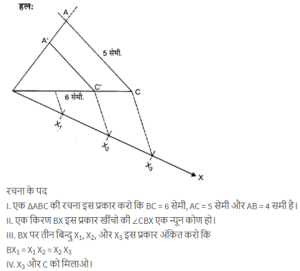

5 cm, 6cm और 7cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 7/5 गुनी हो|
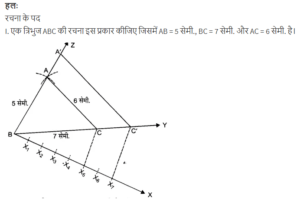

आधार 8cm तथा ऊँचाई 4cm के एक समद्धिबाहू त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ इस समद्धिबाहू त्रिभुज की संगत भुजाओं की 1,1/2 गुनी हों|

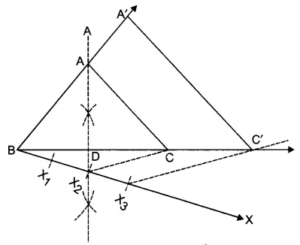

एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cm और angle = 60o हो | फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की 3/4 गुनी हों|
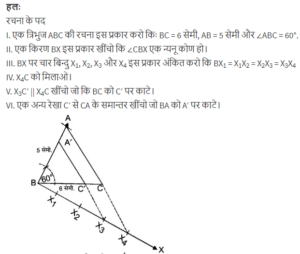

एक त्रिभुज ABC बनाइए, जिसमें BC = 7 cm, angle B = 45° , angle A = 105° हो| फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ त्रिभुज ABC की संगत भुजाओं की 4/3 गुनी हों |
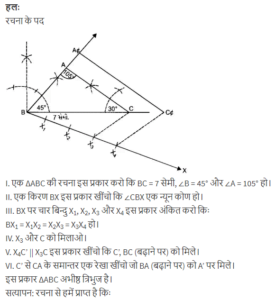

एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm तथा 3 cm लंबाई की हों | फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 5/3 गुनी हों |


6 cm त्रिज्या का एक वृत्त खींचिए | केंद्र से 10 cm दूरी स्थित एक बिन्दु से वृत्त पर स्पर्श रेखा युग्म की रचना कीजिए और उनकी लंबाइयाँ मापिए |

4 cm त्रिज्या के एक वृत्त पर 6 cm त्रिज्या के एक सकेंद्रीय वृत्त के किसी बिन्दु से एक स्पर्श रेखा की रचना कीजिए और उसकी लंबाई मापिए | परिकलन से इस माप की जाँच भी कीजिए |

3 cm त्रिज्या का एक वृत्त खींचिए | इसके किसी भी बढाए गए व्यास पर केंद्र से 7 cm की दूरी पर स्थित दो बिन्दु P और Q लीजिए | इन दोनों बिन्दुओं से वृत्त पर स्पर्श रेखाएँ खींचिए |
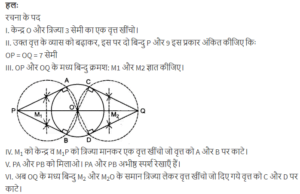

5 cm त्रिज्या के एक वृत्त पर ऐसी दो पार्ष रेखाएँ खींचिए, जो परस्पर 60° के कोण पर झुकी हों |
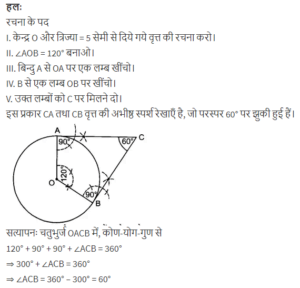
8 cm लंबा एक रेखाखंड AB खींचिए | A को केंद्र मान कर 4 cm त्रिज्या का एक वृत्त तथा B को केंद्र लेकर 3 cm त्रिज्या का एक अन्य वृत्त खींचिए | प्रत्येक वृत्त पर दूसरे वृत्त के केंद्र से स्पर्श रेखाओं की रचना कीजिए |

माना ABC एक समकोण त्रिभुज है, जिसमें AB = 6 cm, BC cm तथा angle =B = 90° है | B से AC पर BD लंब है | बिन्दुओं B,C,D से होकर जाने वाला एक वृत्त खींचा गया है | A से इस वृत्त प[पर स्पर्श रेखा की रचना कीजिए |

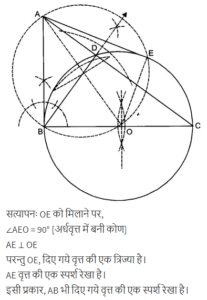
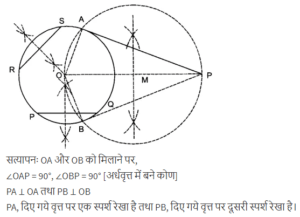
किसी चूड़ी की सहायता से एक वृत्त खींचिए | वृत्त के बाहर एक बिन्दुओं लीजिए | इस बबिन्दु से वृत्त पर स्पर्श रेखाओं की रचना कीजिए |

We hope that class 10 Math Chapter 11 रचनाएँ (Constructions) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 11 रचनाएँ (Constructions) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…