पाठ – 12
वृत्तों से संबंधित क्षेत्रफल
In this post we have given the detailed notes of class 10 Math chapter 12 Areas Related to Circles in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 12 वृत्तों से संबंधित क्षेत्रफल के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 12 |
| Chapter Name | वृत्तों से संबंधित क्षेत्रफल (Areas Related to Circles) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 12 वृत्तों से संबंधित क्षेत्रफल
वृत्त का परिमाप
एक वृत्त के अनुदिश एक बार चलने में तय की गई दूरी उसका परिमाप होता है, जिसे प्रायः परिधि कहा जाता है। वृत्त की परिधि का उसके व्यास के साथ एक अचर अनुपात होता है। इस अचर अनुपात को एक यूनानी अक्षर π (जिसे ‘पाई’ पढ़ा जाता है) से व्यक्त किया जाता है। दूसरे शब्दों में,
परिधि/व्यास = π
या परिधि = व्यास × π
= π × 2r (जहाँ r वृत्त की त्रिज्या है)
= 2πr
नोट:
π का संख्यात्मक मान 22/7 या 3.1416 प्रयोग किया जाता है।
वृत्त का क्षेत्रफल
वृत्त का क्षेत्रफल त्रिज्या के वर्ग का पाई गुना होता है (A = π r²)। इस सूत्र का प्रयोग करते हुए उस वृत्त का क्षेत्रफल आसानी से ज्ञात कर सकते हैं जिसके व्यास या त्रिज्या दी गई हो।
उदाहरण
एक वृत्ताकार खेत पर रु 24 प्रति मीटर की दर से बाड़ लगाने का व्यय रु 5280 है। इस खेत की रु 0-50 प्रति वर्ग मीटर की दर से जुताई कराई जानी है। खेत की जुताई कराने का व्यय ज्ञात कीजिए। (π = 22/7 लीजिए)
हल:
बाड़ की लंबाई (मीटर में) = पूरा व्यवय/दर = 5280/24 = 220
अतः खेत की परिधि = 220 मीटर
इसलिए यदि खेत की त्रिज्या r मीटर है, तो
2πr = 220
या 2 × 22/7 × r = 220
इसलिए, r = (220 × 7)/(2 × 22) = 35
अर्थात् खेत की त्रिज्या 35 मीटर है।
अतः खेत का क्षेत्रफल = π r² = 22/7 × 35 × 35 m²
अब 1 m² खेत की जुताई का व्यय = रु 0.50
अतः खेत की जुताई कराने का कुल व्यय = 22 × 5 × 35 × 0.50 = रु 1925
दो वृत्तों की त्रिज्याएँ क्रमशः 19 cm और 9 cm हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है।
प्रथम वृत्त का परिमाप = 2πr = 2 × 22/7 × 19
दूसरे वृत्त का परिमाप = 2 × 22/7 × 9
तीसरे वृत्त की परिधि = 2πr = 2 × 22/7 × 19 + 2 × 22/7 × 9 = 2 × 22/7 × (19 + 9)
= 2 × 22/7 × 28
2πr = 2 × 22/7 × 28
इसलिए, r = 28 cm
त्रिज्यखंड और वृत्तखंड
त्रिज्यखंड: एक वृत्तीय क्षेत्र का वह भाग जो दो त्रिज्याओं और संगत चाप से घिरा (परिबद्ध) हो, उस वृत्त का एक त्रिज्यखंड कहलाता है।
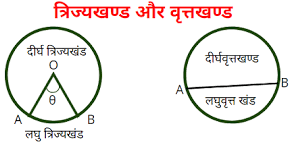
वृत्तखंड: वृत्तीय क्षेत्र का वह भाग जो एक जीवा और संगत चाप के बीच में परिबद्ध हो एक वृत्तखंड कहलाता है।
टिप्पणी
जब तक अन्यथा न कहा जाए, ‘वृत्तखंड’ और ‘त्रिज्यखंड’ लिखने से हमारा तात्पर्य क्रमशः लघु वृत्तखंड और लघु त्रिज्यखंड से होगा।
त्रिज्यखंड का क्षेत्रफल

मान लीजिए OAPB केंद्र O और त्रिज्या R वाले वृत्त का एक त्रिज्यखंड है। मान लीजिए ∠AOB का अंशीय माप θ है।
आप जानते हैं कि एक वृत्त [वस्तुतः एक वृत्तीय क्षेत्र या चकती] का क्षेत्रफल πr² होता है।
एक तरीके से, हम इस वृत्तीय क्षेत्र को केंद्र व् पर 360° का कोण बनाने वाला (अंशीय माप 360) एक त्रिज्यखंड मान सकते हैं। फिर ऐकिक विधि का प्रयोग करके, हम त्रिज्यखंड OAPB का क्षेत्रफल नीचे दर्शाए अनुसार ज्ञात कर सकते हैंः
जब केंद्र पर बने कोण का अंशीय माप 360 है, तो त्रिज्यखंड का क्षेत्रफल = πr²
अतः, जब केंद्र पर बने कोण का अंशीय माप 1 है, तो त्रिज्यखंड का क्षेत्रफल = πr²/360
इसलिए जब केंद्र पर बने कोण का अंशीय माप θ है, तो त्रिज्यखंड का क्षेत्रफल = πr²/360 × θ
इस प्रकार, हम वृत्त के एक त्रिज्यखंड के क्षेत्रफल के लिए, निम्नलिखित संबंध (या सूत्र) प्राप्त करते हैंः
कोण θ वाले त्रिज्यखंड का क्षेत्रफल = θ/360 × πr²
जहाँ r वृत्त की त्रिज्या है और θ त्रिज्यखंड का अंशों में कोण है।
त्रिज्यखंड के संगत चाप की लंबाई
अब एक स्वाभाविक प्रश्न उठता हैः क्या हम इस त्रिज्यखंड की संगत चाप APB की लंबाई ज्ञात कर सकते हैं। हाँ, हम ऐसा कर सकते हैं। पुनः, ऐकिक विधि का प्रयोग करने तथा संपूर्ण वृत्त (360° कोण वाले) की लंबाई 2πr लेने पर,
हम चाप APB की वांछित लंबाई θ/360 × 2πr प्राप्त करते हैं।
अतः कोण θ वाले त्रिज्यखंड के संगत चाप की लंबाई = θ/360 × 2πr
त्रिज्या 4 cm वाले एक वृत्त के त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 30° है। साथ ही, संगत दीर्घ त्रिज्यखंड का क्षेत्रफल भी ज्ञात कीजिए। (π = 3.14 का प्रयोग कीजिए)।
दिया हुआ त्रिज्यखंड OAPB है।
त्रिज्यखंड का क्षेत्रफल = θ/360 × πr²
= 30/360 × 3.14 × 4 × 4 cm²
= 12.56/3 cm² = 4.19 cm²
संगत दीर्घ त्रिज्यखंड का क्षेत्रफल = πr² – त्रिज्यखंड OAPB का क्षेत्रफल
= (3.14 × 16 – 4.19) cm²
= 46.05 cm² = 46.1 cm²
वृत्तखंड का क्षेत्रफल
आइए अब केंद्र और त्रिज्या वाले वृत्तखंड के क्षेत्रफल पर विचार करें। आप देख सकते हैं कि
वृत्तखंड का क्षेत्रफल
= त्रिज्यखंड का क्षेत्रफल का क्षेत्रफल
= θ/360 × 2πr² – ∆OAB का क्षेत्रफल
दिए गए वृत्तखंड का क्षेत्रफल ज्ञात कीजिए, यदि वृत्त की त्रिज्या 21 Cm है और ∠AOB = 120⁰ है। (Π = 22/7 लीजिए)
वृत्तखंड AYB का क्षेत्रफल = त्रिज्यखंड OAYB का क्षेत्रफल – ∆OAB का क्षेत्रफल (1)
अब, त्रिज्यखंड व्।ल्ठ का क्षेत्रफल = 120/360 × 22/7 × 21 × 21 cm² = 462 cm² (2)
∆OAB का क्षेत्रफल ज्ञात करने के लिए OM ⊥ AB खींचिए।
ध्यान दीजिए कि OA = OB है। अतः, RHS सर्वांगसमता से, ∆AMO ≅ ∆BMO है।
इसलिए M जीवा AB का मध्य-बिदु है तथा ∠AOM = ∠BOM = ½ × 120⁰ = 60⁰ है।
मान लीजिए, OM = x cm है।
इसलिए, ∆OMA से OM/OA = cos60⁰ = ½
या x/21 = ½
x = 21/2 cm
अतः OM = ½
साथ ही AM/OA = sin60⁰ = √3/2
अतः AM = 21√3/2 cm
इसलिए AB = 2 AM = 21√3 cm
अतः ∆OAB का क्षेत्रफल = ½ × AB × OM = ½ × 21√3 × 21/2 cm²
= (441√3)/4 cm² (3)
इसलिए वृत्तखंड का क्षेत्रफल = {462 – (441√3)/4} cm² (समीकरण 1, 2 और 3 से)
= 21/4(88 – 21√3) cm²
समतल आकृतियों के संयोजनों के क्षेत्रफल
अभी तक हमने विभिन्न आकृतियों के क्षेत्रफल पृथक-पृथक रूप से ज्ञात किए हैं। अब समतल आकृतियों के कुछ संयोजनों के क्षेत्रफल ज्ञात करने का प्रयत्न करें। हमें इस प्रकार की आकृतियाँ दैनिक जीवन में तथा विभिन्न रोचक डिज़ाइनों के रूप में देखने को मिलती हैं। फूलों की क्यारियाँ, नालियों के ढक्कन, खिड़कियों के डिज़ाइन, मेज़ पोशों पर बने डिज़ाइन आदि ऐसी आकृतियों के कुछ उदाहरण हैं। इन आकृतियों के क्षेत्रफल ज्ञात करने की प्रक्रिया को हम कुछ उदाहरणों द्वारा स्पष्ट करेंगे।
एक वर्ग ABCD जिसकी एक भुजा का माप 14 Cm है। वर्ग के अन्दर भुजाओं को स्पर्श करते हुए चार वृत्त एक दूसरे को स्पर्श करते हुए बनाए गए हैं वृतों को छोड़कर बचे हुए वर्ग का क्षेत्रफल ज्ञात कीजिए।
वर्ग ABCD का क्षेत्रफल = 14 × 14 cm² = 196 cm²
प्रत्येक वृत्त का व्यास = 14/2 = 7 cm
इसलिए त्रिज्या = 7/2 cm
अतः एक वृत्त का क्षेत्रफल = 22/7 × 7/2 × 7/2 cm²
= 154/4 cm²
इस प्रकार 4 वृतों का क्षेत्रफल = 4 × 154/4 cm² = 154 cm²
अतः वृतों को छोड़कर बचे हुए वर्ग का क्षेत्रफल = (196 – 154) cm²
= 42 cm²
वृत्त की परिधि (circumference) –
वृत्त की वक्रीय (curve) सीमा की लंबाई उसका परिमाप
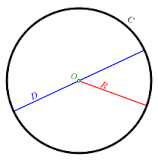
- वृत्त की परिधि का उसके व्यास (diameter) के साथ एक अचर अनुपात (constant ratio) होता है, जिसे हम एक यूनानी अक्षर π (पाई) से दर्शाते हैं।
* परिधि/व्यास = π
* परिधि = व्यास x π
या
* परिधि = 2r x π (r वृत्त की त्रिज्या है)
या
* परिधि = 2πr
- π एक अपरिमेय संख्या (irrational number) है, जिसका दशमलव प्रसार (decimal expansion) अनवसानी अनावृत्ति (non-terminating non recurring) है। फिर भी हम प्रश्नों को हल करने के लिए π का मान 22/7 या 3.14 रखते हैं।
जब दो संयोजित आकृतियों (joint shapes) में से किसी एक या दोनों का क्षेत्रफल ज्ञात करना हो, तो –
- किसी आकृति के अभ्यंतर (interior) में अन्य आकृतियाँ संयोजित हैं, तो पहले बड़ी आकृति का क्षेत्रफल ज्ञात करके अभ्यंतर वाली आकृतियों का क्षेत्रफल घटाओ या अन्य संक्रिया (operation) करो जो कहा गया हो।
- आकृति को ध्यानपूर्वक देखो कि यह किस आकृति का भाग है।
- संयोजित आकृतियों में सम्बन्ध स्थापित करने का प्रयास करें, तभी कोई हल सम्भव है।
Example:
दो वृत्तों की त्रिज्या क्रमशः 19 cm और 9 cm हैं | उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृत्तों की परिधियों के योग के बराबर है |
हल : पहले वृत्त की त्रिज्या R = 19 cm
दुसरे वृत्त की त्रिज्या r = 9 cm
नए वृत्त का परिमाप = पहले वृत्त का परिमाप + दुसरे वृत्त का परिमाप
नए वृत्त का परिमाप = 2πR1 + 2πr2
= 2π(R + r)
= 2π(19 + 9)
= 2 x 22/7 x 28
= 2 x 22 x 4
= 176 cm
दो वृत्तों की त्रिज्याएँ क्रमशः 8 cm और 6 cm हैं | उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल इन दोनों वृत्तों के क्षेत्रफलों के योग के बराबर है |
हल : पहले वृत्त की त्रिज्या R = 8 cm
दुसरे वृत्त की त्रिज्या r = 6 cm
नए वृत्त का परिमाप = पहले वृत्त का परिमाप + दुसरे वृत्त का परिमाप
नए वृत्त का परिमाप = πR2 + πr2
= π(R2 + r2)
= 2π(19 + 9)
= 2 x 22/7 x 28
= 2 x 22 x 4
= 176 cm
आकृति एक तीरंदाजी लक्ष्य को दर्शाती है, जिसमें केंद्र से बाहर की ओर पाँच क्षेत्र GOLD, RED, BLUE, BLACK और WHITE चिन्हित हैं, जिनसे अंक अर्जित किए जा सकते हैं | GOLD अंक वाले क्षेत्र का व्यास 21 cm है तथा प्रत्येक अन्य पट्टी 10.5 cm चौड़ी है | अंक प्राप्त कराने वाले इन पाँचों क्षेत्रों में से प्रत्येक का क्षेत्रफल ज्ञात कीजिए |

हल :


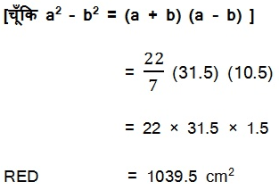



किसी कार के प्रत्येक पहिये का व्यास 80 cm है | यदि यह कार 66 km प्रति घंटे की चाल से चाल रही है, तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाती है ?
हल :
पहिये का व्यास = 80 cm
पहिये की त्रिज्या (r) = 40 cm
कार की चाल = 66 km प्रति घंटा


निम्नलिखित में सही उत्तर चुनिए तथा अपने उत्तर का औचित्य दीजिए :
यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर है, तो उस वृत्त की त्रिज्या है :
(A) 2 मात्रक
(B) π मात्रक
(C) 4 मात्रक
(D) 7 मात्रक
हल : वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप से बराबर हैं –
इसलिए 2 π r = π r2
या 2 = r [दोनों पक्षों का सरलीकरण करने पर ]
अत: वृत्त की त्रिज्या 2 मात्रक है |
उत्तर : (A) 2 मात्रक
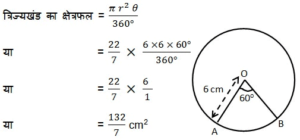
6 cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण 60o है |
हल :
त्रिज्या (r) = 6 cm और कोण θ = 60o
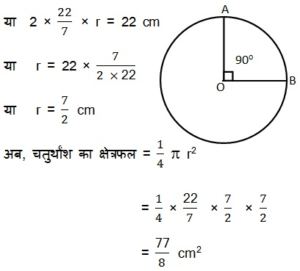
एक वृत्त, के चतुर्थांश का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 cm है |
हल :
परिधि = 22 cm
या 2 π r = 22 cm
एक घड़ी की मिनट की सुई जिसकी लंबाई 14 cm है | इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए |
हल :
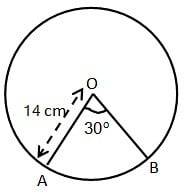
त्रिज्या (r) = मिनट की सुई जिसकी लंबाई = 14 cm

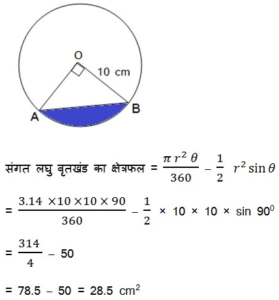
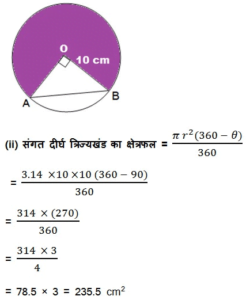
10 सेमी त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर समकोण अंतरित करती है | निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
(i) संगत लघु वृत्तखंड (ii) संगत दीर्घ त्रिज्यखंड
हल :
(i) संगत लघु वृतखंड का क्षेत्रफल
त्रिज्या (r) = 10 cm
θ = 90०
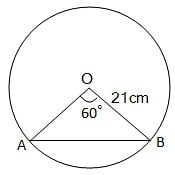
त्रिज्या 21 cm वाले वृत्त का एक चाप केंद्र पर 60o का कोण अंतरित करता है | ज्ञात कीजिए :
(i) चाप की लंबाई
(ii) चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल
(iii) संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल
हल : त्रिज्या (r) = 21 cm
θ = 60०


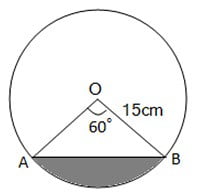
15 cm त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर 60o का कोण अंतरित करती है | और दीर्घ वृत्तखंड़ों के क्षेत्रफल ज्ञात कीजिए।


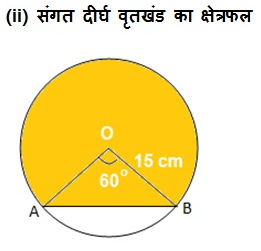

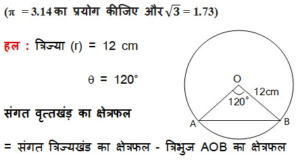
त्रिज्या 12 cm वाले एक वृत्त की कोई जीवा केंद्र पर 120o का कोण अंतरित करती है | संगत वृत्तखंड़ का क्षेत्रफल ज्ञात कीजिए |
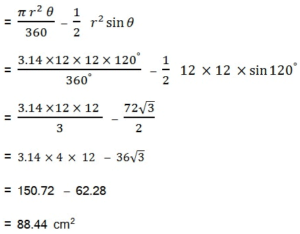
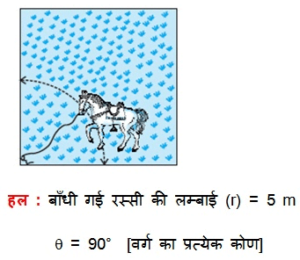
15 m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े को 5 m लंबी रस्सी से बाँध दिया गया है ( देखिए आकृति 12.11) | ज्ञात कीजिए :
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोडा चार सकता है |
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को 5 m लंबी रस्सी के स्थान पर 10 m लंबी रस्सी से बाँध दिया जाए | (π = 3.14 का प्रयोग कीजिए )

(ii) घोड़े द्वारा चरे जा सकने वाले क्षेत्र का क्षेत्रफल जब रस्सी की लंबाई 10 m हो –

एक वृताकार ब्रुच (brooch) को चाँदी के तार से बनाया जाना है जिसका व्यास 35 mm है | तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिज्यखंडों में विभाजित करता है जैसाकि आकृति 12.12 में दर्शाया गया है | तो ज्ञात कीजिए :
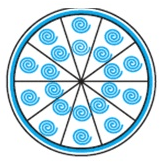
(i) कुल वांछित चाँदी के तार की लंबाई
(ii) ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल


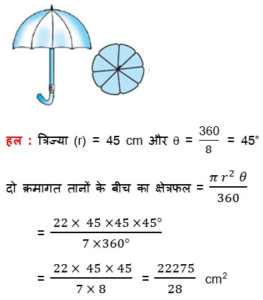
एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लगे हुए हैं (देखिए आकृति 12.13 )| छतरी को 45 cm त्रिज्या वाला एक सपाट वृत्त मानते हुए, इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए |
किसी कार के दो वाइपर (wipers) हैं, परस्पर कभी आच्छादित नहीं होते हैं | प्रत्येक वाइपर की पट्टी की लंबाई 25 cm है और 115o के कोण तक घूम कर सफाई कर सकता है | पट्टियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ़ हो जाता है, वह ज्ञात कीजिए ।

जहाजों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए, एक लाइट हाउस (light house ) 80o कोण वाले एक त्रिज्यखंड में 16.5 km की दूरी तक लाल रंग का प्रकाश फैलाता है | समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाजों को चेतावनी दी जा सके ।

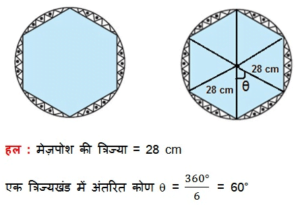
एक गोल मेज़पोश पर छः समान डिज़ाइन बने हुए हैं जैसाकि आकृति 12.14 में दर्शाया गया है । यदि मेज़पोश की त्रिज्या 28 cm है, तो 0.35 रू. प्रति वर्ग सेंटीमीटर की दर से इन डिजाइनों को बनाने की लागत ज्ञात कीजिए ।

We hope that class 10 Math Chapter 12 वृत्तों से संबंधित क्षेत्रफल (Areas Related to Circles) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 12 वृत्तों से संबंधित क्षेत्रफल (Areas Related to Circles) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…