पाठ – 13
पृष्ठीय क्षेत्रफल और आयतन
In this post we have given the detailed notes of class 10 Math chapter 13 Surface Areas and Volumes in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 13 पृष्ठीय क्षेत्रफल और आयतन के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 13 |
| Chapter Name | पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 13 पृष्ठीय क्षेत्रफल और आयतन
घनाभ
घनाभ (क्यूब्वायड) या आयतफलकी वह समान्तरषटफलक है जिसका प्रत्येक फलक आयताकार हो। जब तीनों बीमा (लम्बाई, चौड़ाई, ऊँचाई) समान हों तो वह आकार घन (क्यूब) कहलाता है। ईंट, आयतफलकी का सबसे अच्छा उदाहरण है।
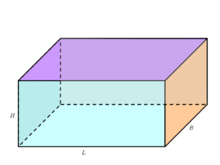
घनाभ के सूत्र
घनाभ का आयतन = लम्बाई × चौड़ाई × ऊँचाई
घनाभ का आयतन = l × b × h.
घनाभ का परिमाप = 2(l + b) × h.
घनाभ के समस्त पृष्ठों का क्षेत्रफल = 2(लम्बाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लम्बाई)
घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(lb + bh + hl)
घनाभ के विकर्ण = √(लम्बाई)² + (चौड़ाई)² + (ऊँचाई)²
घन
घन का आयतन = भुजा × भुजा × भुजा = भुजा3 (भुजा पर घतांक 3 ) घन इकाई / घन यूनिट होता है । जो कि घनाभ के आयतन = लम्बाई × चौड़ाई × ऊंचाई घन इकाई /घन यूनिट का ही एक रूप होता है । घन एक ऐसी त्रिआयामी आकृति को कहा जाता है जिसकी लम्बाई, चौड़ाई एवं ऊँचाई सामान होती हैं।
घन का आयतन = भुजा × भुजा x भुजा या भुजा3
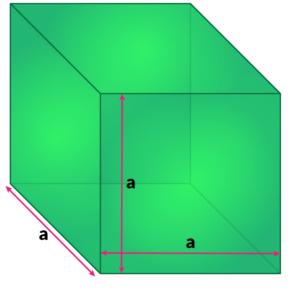
बेलन
बेलन एक ऐसी त्रिआयामी(3d) ठोस आकृति होती है जोकि दो वृत्त एवं एक वक्र आयत से मिलकर बना होता है। इसके दो सिरे सामान त्रिज्या वाले वृत्त होते हैं एवं पार्श्व प्रष्ठ वक्र(curved) होता है।
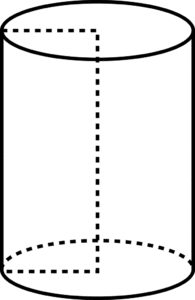
समकोणीय एवं परोक्ष बेलन
समकोणीय बेलन एक ऐसा बेलन होता है जिसका अक्ष आधार को समकोण पर काटता है। लेकिन अगर कोई अक्ष आधार को समकोण पर नहीं काट रहा है तो फिर वह बेलन एक परोक्ष बेलन होगा।
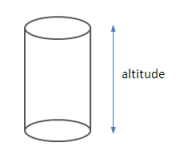
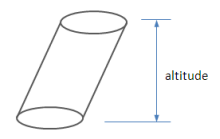
बेलन का आयतन एवं क्षेत्रफल
अगर हमें एक बेलन का पूर्ण पृष्ठीय क्षेत्रफल निकालना है तो हमें इसे सबसे पहले तीन टुकड़ों में बांटना पडेगा। ये तीन टुकड़े होंगे दो सर्वांग्सम एवं समान्तर वृत्त एवं वक्र पृष्ठ जो कि एक आयत है।
जैसा कि हम जानते हैं कि एक वृत्त का क्षेत्रफल πr2 होता है। अगर हमारे पास दो वृत्त हैं तो फिर इनका कुल क्षेत्रफल होगा।
= 2 πr2
अब हमें बचे हुए आयत का क्षेत्रफल निकालना है जोकि होता है लम्बाई * चौड़ाई । यहाँ हमारे पास आयत की लम्बाई तो बेलन की ऊंचाई मानी जायेगी। अब जो आयत की चौड़ाई है वह वृत्त के परिमाप के सामान होगी जोकि 2πr होगा। अतः इस आयत का क्षेत्रफल होगा।
= 2πr × h
जब हम इन दोनों टुकड़ों को जोड़ देंगे तो इस बेलन का पूर्ण पृष्ठीय क्षेत्रफल होगा।
= 2 πr2 + 2πr × h
अतः बेलन का पूर्ण पृष्ठीय क्षेत्रफल = 2πr(r + h)
बेलन का वक्र पृष्ठीय क्षेत्रफल
जैसा कि हम जानते हैं की बेलन का वक्र पृष्ठ सिर्फ एक आयत होता है अतः हमें सिर्फ उस आयत का क्षेत्रफल ज्ञात करना होगा। यही क्षेत्रफल इस बेलन का वक्र पृष्ठीय क्षेत्रफल होगा।
जैसा की हम जानते हैं एक आयत का क्षेत्रफल होता है :
लम्बाई × चौड़ाई
यहाँ आयत की लम्बाई तो बेलन की ऊंचाई हो जायेगी लेकिन आयत की चौड़ाई वृत्त का परिमाप होगा। अतः हमें वह ज्ञात करना होगा। जैसा कि हम जानते हैं की एक वृत्त का परिमाप होगा :
= 2πr
अब हम वृत्त के परिमाप को एवं बेलन की ऊँचाई को गुना कर देंगे जिससे हमारे पास बेलन का वक्र पृष्ठीय क्षेत्रफल या आयत का क्षेत्रफल आया जाएगा।
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πr × h
बेलन का आयतन
आयतन(volume) का मतलब होता है की कोई त्रिआयामी आकृति अपने अन्दर कितना द्रव्य रख सकती है। इसे हम अक्सर m3 या cm3 से व्यक्त करते हैं।
एक बेलन का आयतन (volume of cylinder) निकालना बहुत सरल होता है। इसके लिए हमें बस वृत्त के क्षेत्रफल को बेलन की ऊंचाई से गुना करना पड़ता है।
वृत्त का क्षेत्रफल = πr2
इसे ऊंचाई (h) से गुना करने पर :
बेलन का आयतन = πr2h
शंकु
शंकु (Cone) एक ऐसी त्रिआयामी (3d) आकृति है जिसका जिसका आधार गोलाकार होता है तथा जिसका शीर्ष एक बिंदु होता है। यदि किसी Shanku का आधार एक वृत्त हो तो उसे हम लम्ब वृत्तीय शंकु कहते है। यह शंकु समान आधार और ऊंचाई वाले बेलन के ![]() भाग के बराबर होता है।
भाग के बराबर होता है।
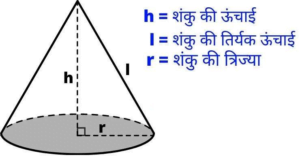
एक शंकु में केवल एक आधार होता है एवं गोलाकार होता है। यह Cone का नीचे का हिस्सा होता है। इसे शंकु का फलक भी कहा जाता है।
एक शंकु में एक शीर्ष होता है। शंकु का शीर्ष एक बिंदु होता है।
एक शंकु की चौड़ाई उसके गोलाकार फलक का व्यास होता है अर्थात शंकु के गोलाकार भाग का व्यास ही शंकु की चौड़ाई होती है।
शंकु का क्षेत्रफल
शंकु का क्षेत्रफल दो प्रकार का होता है एक पूर्ण पृष्ठीय क्षेत्रफल तथा दूसरा वक्र पृष्ठीय क्षेत्रफल। आइये अब Shanku के क्षेत्रफल को निकालने के लिए महत्वपूर्ण सूत्रों को जाने।
शंकु का वक्र पृष्ठीय क्षेत्रफल –
शंकु का वक्र पृष्ठीय क्षेत्रफल निकालने के लिए हमें शंकु की त्रिज्या तथा शंकु की तिर्यक ( तिरछी ) ऊंचाई का पता होना चाहिए। तभी हम शंकु का वक्र पृष्ठीय क्षेत्रफल निकाल सकते हैं।
शंकु का वक्र पृष्ठिय क्षेत्रफल = πRL
अगर हमें शंकु का वक्र पृष्ठीय क्षेत्रफल तथा त्रिज्या दी गयी हो तो हम शंकु की तिर्यक ऊंचाई निकाल सकते हैं। इसके लिए हम शंकु के वक्र पृष्ठीय क्षेत्रफल को इसके सूत्र के बराबर लिख कर और थोड़ी सी कैल्कुलेशन करके मान ज्ञात कर सकते हैं। ऐसा ही हम अन्य सूत्रों के साथ भी कर सकते हैं।
शंकु के पूर्ण पृष्ठीय क्षेत्रफल
शंकु का पूर्ण पृष्ठीय क्षेत्रफल निकालने का मतलब होता है शंकु के चारों तरफ का क्षेत्रफल। इसमे शंकु के तल में मौजूद वृत का क्षेत्रफल भी शामिल होता है। शंकु का पूर्ण पृष्ठीय क्षेत्रफल निकालने के लिए हम सूत्र का उपयोग करते हैं। Cone के पूर्ण पृष्ठीय क्षेत्रफल में हम शंकु तथा वृत के क्षेत्रफल को जोड़ देते हैं। क्योंकि Shanku के तल में वृत भी होता है।
जब हम शंकु के वक्र पृष्ठीय क्षेत्रफल में वृत्त का क्षेत्रफल भी जोड़ देते हैं तो हमें शंकु का पूर्ण पृष्ठीय या सम्पूर्ण पृष्ठीय क्षेत्रफल प्राप्त होता है।
शंकु के वक्र पृष्ठ का क्षेत्रफल + वृत्त का क्षेत्रफल = शंकु का पूर्ण पृष्ठीय क्षेत्रफल
![]()
अन्तः शंकु का पूर्ण पृष्ठीय क्षेत्रफल = πr ( l + r )
यहाँ R या r का मतलब शंकु के आधार की त्रिज्या होता है तथा L या l का मतलब शंकु की तिर्यक अर्थात तिरछी ऊंचाई होता है। पाई का मान हम ![]()
या 3.14 लेते हैं।
अगर किसी सवाल या प्रश्न में हमें शंकु का पृष्ठीय क्षेत्रफल निकालने के लिए कहा जाए तो हम शंकु का पूर्ण पृष्ठीय क्षेत्रफल निकालेंगे ना कि वक्र पृष्ठीय क्षेत्रफल।
शंकु का आयतन
शंकु की बनावट के आधार पर हम Shanku का आयतन शंकु के समान आधार वाले एक बेलन के आयतन का तीसरा हिस्सा मानते हैं। जितना समान आधार वाले बेलन का आयतन होगा उसका तीसरा हिस्सा उसी आधार वाले शंकु का आयतन होगा।
बेलन का आयतन = ![]()
शंकु का आयतन = ![]()
इस प्रकार से Shanku का आयतन बेलन के आयतन का तीसरा हिस्सा होगा। इसलिए हम बेलन के आयतन को 3 से भाग कर देते हैं और हमें शंकु के आयतन का सूत्र मिल जाएगा।
शंकु का आयतन ![]()
गोला
गोले के सभी सूत्रों को याद करने से पहले जरुरी है कि गोले से सम्बंधित सभी प्रकार के मूल बातों को जान ले. जैसे कि गोला किसे कहते हैं अथवा गोले की परिभाषा क्या है, गोले की त्रिज्या, गोले का व्यास तथा गोले कितने प्रकार के होते हैं।
गोले का केंद्र व त्रिज्या
केंद्र (Center):- जिस निश्चित बिंदु या नियत बिंदु से एक त्रि-आयामी गोले का निर्माण होता है, वह नियत बिंदु गोले का केंद्र कहलाता है। जैसा की ऊपर दिए गए चित्र नियत बिंदु O गोले का केंद्र (Center) है।
त्रिज्या की माप :- किसी भी गोले की केंद्र से उसकी सतह के बीच के रेखाखंड की लम्बाई को गोले की त्रिज्या कहते हैं। जैसा की ऊपर दिए गए गोले की चित्र से स्पष्ट हो रहा है केंद्र बिंदु (O) तथा सतह बिंदु (A) के बीच की रेखाखंड की लम्बाई ही गोले की त्रिज्या की माप है। गोले के त्रिज्या की माप से गोले का आयतन तथा सम्पूर्ण वक्रपृष्ठ का क्षेत्रफल (Gole ka Formula) आसानी से निकाल सकते हैं।
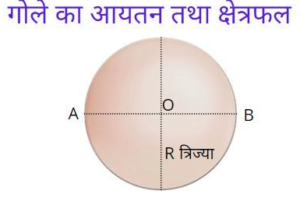
गोले का व्यास (Diameter of Sphere):- किसी भी गोले के सतह पर स्थित एक बिंदु से दुसरे बिंदु पर जाने वाली रेखाखंड की लम्बाई जो की केंद्र बिंदु से होकर गुजरती है, गोले का व्यास (Diameter of Gola) कहलाता है। ऊपर दिए चित्र में देख सकते हैं की रेखाखंड AB गोले का व्यास है जो की गोले के केंद्र बिंदु से होकर गुजर रही है।
गोले की व्यास की लम्बाई या सूत्र = 2 x गोले की त्रिज्या
गोले का व्यास (Diameter of Sphere):- किसी भी गोले के सतह पर स्थित एक बिंदु से दुसरे बिंदु पर जाने वाली रेखाखंड की लम्बाई जो की केंद्र बिंदु से होकर गुजरती है, गोले का व्यास (Diameter of Gola) कहलाता है। ऊपर दिए चित्र में देख सकते हैं की रेखाखंड AB गोले का व्यास है जो की गोले के केंद्र बिंदु से होकर गुजर रही है।
गोले की व्यास की लम्बाई या सूत्र = 2 x गोले की त्रिज्या
एक गोले के बाहरी सतह द्वारा घिरा हुआ भाग, गोले का वक्रपृष्ठ क्षेत्रफल होता है. चूँकि एक गोले में में कोई किनारा या कोना नहीं होता है, इसीलिए एक गोले का वक्रपृष्ठ क्षेत्रफल ही गोले के सम्पूर्ण क्षेत्रफल होता है. अतः निम्नलिखित संबंधो द्वारा एक गोले का सम्पूर्ण वक्र पृष्ठ का क्षेत्रफल का फार्मूला या सूत्र को परिभाषित करते हैं।
माना कि एक गोला है जिसका केंद्र बिंदु O है, त्रिज्या R है तथा व्यास की लम्बाई D है, अतः
गोले का सम्पूर्ण वक्रपृष्ठ का क्षेत्रफल = 4 πR2
जहाँ π = 3.14
किसी भी गोले (Sphere) का क्षेत्रफल का फार्मूला (Formula) जब गोले का व्यास (Diameter) दिया हुआ हो.
Sphere ka Kshetrafal Formula = π D2
गोला का आयतन का सूत्र
किसी भी एक गोले के आयतन निम्नलिखित सूत्र द्वारा प्राप्त किया जा सकता है. चूँकि गोला दो प्रकार का होता है, ठोस गोला तथा खोखला गोला. अतः दोनों ही गोले का आयतन का फार्मूला निकालने के लिए गोले के त्रिज्या (खोखले गोले के लिए बाह्य तथा अन्तः त्रिज्या) का माप तथा व्यास की लम्बाई पता होना चाहिए.
ठोस गोला वह गोला होता है जो कि अंदर से भरा हुआ होता है, अर्थात गोले के आंतरिक भाग खोखला नहीं होता है। गोले का उदाहरण – पृथ्वी, उपग्रह, बॉल बेअरिंग.
माना कि ठोस गोले का त्रिज्या R तथा व्यास D है, तब
गोले का आयतन का फार्मूला ![]()
यदि गोले का व्यास का माप दिया हो उस स्थिति में गोले का आयतन का सूत्र
गोले का आयतन का सूत्र ![]()
खोखले गोला का आयतन का सूत्र
ऐसा गोला जो की अंदर से खाली या खोखला होता है वह खोखला गोला या गोलीय कोश कहलाता है. गोलीय कोश का उदाहरण- बॉल, बलून आदि.
किसी भी खोखले गोला या गोलीय कोश के आयतन का सूत्र (Formula) निकालने के लिए गोले का आतंरिक त्रिज्या तथा बाह्य त्रिज्या का माप पता होना चाहिए.
माना कि खोखले गोले का आंतरिक त्रिज्या (r) तथा बाह्य त्रिज्या R है, तब
खोखले गोले का आयतन का सूत्र ![]()
यदि खोखले गोले का आतंरिक तथा बाह्य व्यास का माप क्रमशः d तथा D है तब,
खोखले गोले का आयतन का सूत्र 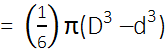
अर्द्ध गोला (Hemisphere)
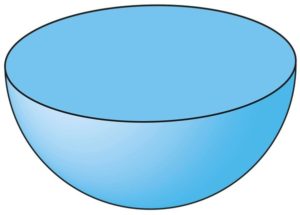
जैसा की इसके नाम से ही प्रतीत हो रहा है, एक अर्ध गोला पूरे गोले का आधा भाग होता है। जब एक गोले को दो भागों में बांटा जाता है उससे हमें जो आकृति मिलती है वह अर्धगोला कहलाती है। इसकी एक सतह चपटी(flat) होती है एवं दूसरी सतह वक्र(curved) होती है।
ऊपर दी गयी आकृति में जैसा कि आप देख सकते हैं यहाँ इस त्रिआयामी आकृति की ऊपर वाली सतह चपटी(flat) है एवं जो दूसरी सतह है वह वक्र(curved) है। अतः यह एक अर्धगोला कहलायेगा।
अर्ध गोले की दो ही सतह होती हैं। पहली सतह चपटी होती है एवं दूसरी सतह वक्र अर्थात curved होती है। चपटी सतह उस अर्ध गोले का आधार कहलाती है।
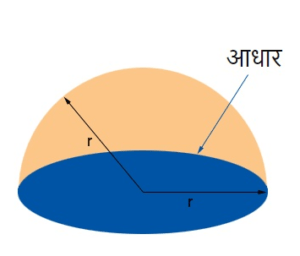
एक अर्धगोले की जो वृत्त के आकार सतह होती है उसके हर बिंदु की केंद्र से दूरी समान होती है।
अर्ध गोला एक पूरे गोले को दो भागों में विभाजित किये जाने से बना होता है।
एक पूरे गोले को जब हम दो भागों में विभाजित करते हैं तो हमारे पास दो अर्धगोले हो जाते हैं।
अर्धगोले का आयतन
जैसा कि हम जानते हैं एवं पहले भी देख चुके हैं एक अर्ध गोला पूरे गोले का आधा भाग होता है अतः इसका आयतन भी पूरे गोले का आयतन का आधा होगा।
अतः
अर्ध गोले का आयतन = ![]() × गोले का आयतन
× गोले का आयतन
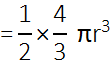
अतः अर्ध गोले का आयतन = ![]()
अर्धगोले का पूर्ण पृष्ठीय क्षेत्रफल
एक अर्ध गोले का वक्र पृष्ठीय क्षेत्रफल एक पूर्ण गोले के क्षेत्रफल को आधा करने पर निकल गया। अब हमें इसका पूर्ण पृष्ठीय क्षेत्रफल निकालना है तो बस इसके आधार का क्षेत्रफल जोड़ना होगा।
अर्ध गोले का पूर्ण पृष्ठीय क्षेत्रफल = अर्ध गोले का वक्र पृष्ठीय क्षेत्रफल + आधार का क्षेत्रफल ![]()
अतः अर्ध गोले का पूर्ण पृष्ठीय क्षेत्रफल ![]() वर्ग unit
वर्ग unit
ठोसों के संयोजन का पृष्ठीय क्षेत्रफल
पृष्ठीय क्षेत्रफल किसी 3D आकृति पर मौजूद सभी फलकों (या सतहों) के क्षेत्रफल का योग होता है। कुछ ठोस एक से अधिक आकृतियों के संयोजन से बनी होती हैं। इस प्रकार की आकृतियों का पृष्ठीय क्षेत्रफल ज्ञात करने के लिए सभी संयोजित आकृतियों का क्षेत्रफल अलग-अलग ज्ञात करके सभी क्षेत्रफल का योग करें।
उदाहरण के लिए पानी या केरोसिन के टैंकर को लेते हैं जो बीच में बेलनाकार तथा दोनों तरफ अर्द्धगोलाकार होता है। इसलिए इस ठोस का संपूर्ण पृष्ठीय क्षेत्रफल तीनों भागों के वक्र पृष्ठीय क्षेत्रफलों के योग के बराबर होगा। इससे हमें प्राप्त होता हैः
ठोस का संपूर्ण पृष्ठीय क्षेत्रफल = एक अर्धगोले का वक्र पृष्ठीय क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल + दूसरे अर्धगोले का वक्र पृष्ठीय क्षेत्रफल
उदाहरण
रशीद को जन्मदिन के उपहार के रूप में एक लट्टू मिला, जिस पर रंग नहीं किया गया था। वह इस पर अपने मोमिया रंगों से रंग करना चाहता है। यह लट्टू एक शंकु के आकार का है जिसके ऊपर एक अर्धगोला अध्यारोपित है। लट्टू की पूरी ऊँचाई 5 cm है और इसका व्यास 3.5 cm है। उसके द्वारा रंग किया जाने वाला क्षेत्रफल ज्ञात कीजिए। 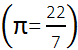 लीजिए।
लीजिए।
हल:
यह लट्टू दो आकृतियों के संयोजन से बना है। एक अर्द्धगोला तथा उसके ऊपर शंकु है। अतः, हम वहाँ पर प्राप्त परिणाम को सुविधाजनक रूप से यहाँ प्रयोग कर सकते हैं। अर्थात्
लट्टू का वक्र पृष्ठीय क्षेत्रफल = अर्धगोले का वक्र पृष्ठीय क्षेत्रफल + शंकु का वक्र पृष्ठीय क्षेत्रफल
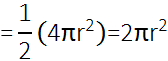
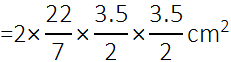
साथ ही, शंकु की ऊँचाई = लट्टू की ऊँचाई – अर्धगोलीय भाग की ऊँचाई (त्रिज्या)
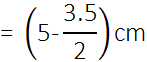
अतः शंकु की तिर्यक ऊँचाई ![]()
इसलिए शंकु का वक्र पृष्ठीय क्षेत्रफल ![]()
लट्टू का वक्र पृष्ठीय क्षेत्रफल = 2 × 22/7 × 3.5/2 × 3.5/2 cm² + 22/7 × 3.5/2 × 3.7 cm²
= 39.6 cm²
उदाहरण
एक आकृति सजावट के लिए प्रयोग होने वाला ब्लॉक दो ठोसों से मिलकर बना है। इनमें से एक घन है और दूसरा अर्धगोला है। इस ब्लॉक का आधार 5 cm कोर या किनारे वाला एक घन है और उसके ऊपर लगे हुए अर्धगोले का व्यास 4.2 cm है। इस ब्लॉक का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 22/7 लीजिए।)
हल:
घन का संपूर्ण पृष्ठीय क्षेत्रफल = 6 × (कोर)² = 6 × 5 × 5 cm² = 150 cm²
अब, घन का वह भाग जिस पर अर्धगोला लगा हुआ है पृष्ठीय क्षेत्रफल में सम्मिलित नहीं होगा।
अतः ब्लॉक का पृष्ठीय क्षेत्रफल = घन का संपूर्ण पृष्ठीय क्षेत्रफल – अर्धगोले के आधार का क्षेत्रफल + अर्धगोले का पृष्ठीय क्षेत्रफल
= 150 – πr² + 2πr² = (150 + πr²) cm²
= 150 cm² + 22/7 × 4.2 × 4.2 cm²
= 150 cm² + 13.86 cm² = 163.86 cm²
ठोसों के संयोजन का आयतन
इस अनुच्छेद में यह ज्ञात करने की कोशिश करेंगे कि इस प्रकार के ठोसों के आयतन किस प्रकार परिकलित किए जाते हैं। ध्यान दीजिए कि पृष्ठीय क्षेत्रफल परिकलित करने में हमने दोनों घटकों (ठोसों) के पृष्ठीय क्षेत्रफलों को जोड़ा नहीं था क्योंकि इनको मिलाने की प्रक्रिया में पृष्ठीय क्षेत्रफल का कुछ भाग लुप्त हो गया था। परंतु आयतन परिकलित करने की स्थिति में ऐसा नहीं होगा। दो आधारभूत ठोसों के संयोजन से बने ठोस का आयतन वास्तव में दोनों घटकों के आयतनों के योग के बराबर होता है, जैसाकि हम नीचे दिए उदाहरण में देखेंगे।
उदाहरण
शांता किसी शेड में एक उद्योग चलाती है। यह शेड एक घनाभ के आकार का है जिस पर एक अर्धबेलन आरोपित है। यदि इस शेड के आधार की विमाएँ 7 m × 15 m हैं तथा घनाभाकार भाग की ऊँचाई 8 m है तो शेड में समावेशित हो सकने वाली हवा का आयतन ज्ञात कीजिए। पुनः यदि यह मान लें कि शेड में रखी मशीनरी 300 m³ स्थान घेरती है तथा शेड के अंदर 20 श्रमिक हैं जिनमें से प्रत्येक 0.08 m³ के औसत से स्थान घेरता है तब शेड में कितनी हवा होगी? (π = 22/7 लीजिए।)
हल
शेड के अंदर हवा का आयतन (जब इसमें कोई व्यक्ति या मशीनरी नहीं है) घनाभ के अंदर की हवा और अर्धबेलन के अंदर की हवा के आयतनों को मिला कर प्राप्त होगा। अब, घनाभ की लंबाई, चौड़ाई और ऊँचाई क्रमशः 15 m, 7 m और 8 m हैं। साथ ही, अर्धबेलन का व्यास 7 m और ऊँचाई 15 m है।
इसलिए वांछित आयतन = घनाभ का आयतन + ½ बेलन का आयतन
आगे, मशीनरी द्वारा घेरा गया स्थान = 300 m³
तथा 20 श्रमिकों द्वारा घेरा गया स्थान = 20 × 0.08 m³ = 1.6 m³
अतः, शेड में उस समय हवा का आयतन, जब उसमें मशीनरी और श्रमिक हैं
= 1128.75 – (300.00 + 1.60) = 827.15 m³
उदाहरण
एक जूस बेचने वाला अपने ग्राहकों को जिन गिलासों से जूस देता था। उस बेलनाकार गिलास का आंतरिक व्यास 5 cm था, परंतु गिलास के निचले आधार (तली) में एक उभरा हुआ अर्धगोला था, जिससे गिलास की धारिता कम हो जाती थी। यदि एक गिलास की ऊँचाई 10 cm थी, तो गिलास की आभासी धारिता तथा उसकी वास्तविक धारिता ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल
चूँकि गिलास का आंतरिक व्यास = 5 cm है और ऊँचाई = 10 cm है, इसलिए गिलास की आभासी धारिता = πr²h
= 3.14 × 2.5 × 2.5 × 10 cm³ = 196.25 cm³
परंतु इसकी वास्तविक धारिता उपरोक्त धारिता से आधार में बने अर्धगोले के आयतन के बराबर कम है।
अर्थात् कमी बराबर है 2/3 πr³ = 2/3 × 3.14 × 2.5 × 2.5 × 2.5 cm³
= 32.71 cm³
अतः गिलास की वास्तविक धारिता = आभासी धारिता – अर्धगोले का आयतन
= 196.25 cm³ – 32.71 cm³
= 163.54 cm³
उदाहरण
एक ठोस खिलौना एक अर्धगोले के आकार का है जिस पर एक लंब वृत्तीय शंकु आरोपित है। इस शंकु की ऊँचाई 2 cm है और आधार का व्यास 4 cm है। इस खिलौने का आयतन निर्धारित कीजिए। यदि एक लंब वृत्तीय बेलन इस खिलौने के परिगत हो तो बेलन और खिलौने के आयतनों का अंतर ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल
मान लीजिए BPC अर्धगोला है तथा ABC अर्धगोले के आधार पर खड़ा एक शंकु है। अर्धगोले (और शंकु की भी) की त्रिज्या = ½ × 4 cm = 2 cm इसलिए खिलौने का आयतन = 2/3 πr³ + 1/3 πr²h
= [2/3 × 3.14 × (2)³ + 1/3 × 3.14 × (2)² × 2] cm³
= 25.12 cm³
अब, मान लीजिए कि दिए गए ठोस के परिगत लंब वृत्तीय बेलन है। इस लंब वृत्तीय बेलन के आधार की त्रिज्या = HP = BO = 2 cm है तथा इसकी ऊँचाई
EH = AO + OP = (2 + 2) cm = 4 cm है।
अतः, वांछित आयतन = लंब वृत्तीय बेलन का आयतन – खिलौने का आयतन
= (3.14 × 22 × 4 – 25.12) cm³
= 25.12 cm³
इस प्रकार, दोनों आयतनों का अंतर = 25.12 cm³ है।
एक ठोस का एक आकार से दूसरे आकार में रूपांतरण
एक ठोस आकृति को अन्य आकार के दूसरे ठोस आकृति में परिवर्तित करने पर आकर में रूपांतरण हो जाता हैं जबकि आयतन में किसी प्रकार का कोई परिवर्तन नहीं होता है। उदाहरण के लिए पांच लीटर की बाल्टी से पानी एक गोलाकार घड़े में डाला जाता है तब आकृति में रूपांतरण होता है जबकि आयतन एक समान रहता है। एक उदाहरण केमाध्यम से इसे समझने का प्रयास करते हैं।
उदाहरण
मॉडल बनाने वाली मिट्टी से ऊँचाई 24 cm और आधार त्रिज्या 6 cm वाला एक शंकु बनाया गया है। एक बच्चे ने इसे गोले के आकार में बदल दिया। गोले की त्रिज्या ज्ञात कीजिए।
हल:
शंकु का आयतन = 1/3 × π × 6 × 6 × 24 cm³
यदि गोले की त्रिज्या r है तो उसका आयतन 4/3 πr³ है।
चूँकि शंकु के रूप में और गोले के रूप में मिट्टी के आयतन बराबर हैं, इसलिए
= 4/3 πr³ = 1/3 × π × 6 × 6 × 24
अर्थात् r³ = 3 × 3 × 24 = 3³ × 2³
अतः r = 3 × 2 = 6
इसलिए, गोले की त्रिज्या 6 cm है।
उदाहरण
सेल्वी के घर की छत पर बेलन के आकार की एक टंकी है। इस टंकी में एक भूमिगत टंकी में भरे पानी को पंप द्वारा पहुँचा कर टंकी को भरा जाता है। यह भूमिगत टंकी एक घनाभ के आकार की है, जिसकी विमाएँ 1.57 m × 1.44 m × 95 cm हैं। छत की टंकी की त्रिज्या 60 cm है और ऊँचाई 95 cm है। यदि भूमिगत टंकी पानी से पूरी भरी हुई थी, तो उससे छत की टंकी को पूरा भरने के बाद भूमिगत टंकी में पानी कितनी ऊँचाई तक रह जाएगा? छत की टंकी की धारिता की भूमिगत टंकी की धारिता से तुलना कीजिए। (π = 3.14 लीजिए।)
हल:
छत की टंकी का आयतन = भूमिगत टंकी से निकाले गए पानी का आयतन
अब, छत की टंकी (बेलन) का आयतन = πr²h
= 3.14 × 0.6 × 0.6 × 0.95 m³
भूमिगत टंकी के पानी से पूरी भरी होने पर पानी का आयतन
= l × b × h = 1.57 × 1.44 × 0.95 m³
छत की टंकी को पानी से पूरा भरने के बाद भूमिगत टंकी में शेष बचे पानी का आयतन
= [(1.57 × 1.44 × 0.95) – (3.14 × 0.6 × 0.6 × 0.95)] m³ = (1.57 × 0.6 × 0.6 × 0.95 × 2) m³
इसलिए, भूमिगत टंकी में शेष बचे पानी की ऊँचाई = (उसमें बचे पानी का आयतन)/(l × b)
= (1.57 × 0.6 × 0.6 × 0.95 × 2)/(1.57 × 1.44) m
= 0.475 m = 47.5 cm
साथ ही, (छत की टंकी की धारिता)/ (भूमिगत की टंकी की धारिता)
= (3.14 × 0.6 × 0.6 × 0.95)/ (1.57 × 1.44 × 0.95) = 1/2
अतः, छत की टंकी की धारिता भूमिगत टंकी की धारिता की आधी है।
शंकु का छिन्नक
एक दिए हुए शंकु को उसके आधार के समांतर किसी तल द्वारा काटते हैं और इस तल के एक ओर बने शंकु को हटा देते हैं, तो तल के दूसरी ओर बचे शंकु के भाग को शंकु का छिन्नक कहते हैं। हम शंकु के छिन्नक के पृष्ठीय क्षेत्रफल और आयतन किस प्रकार ज्ञात कर सकते हैं? इसे एक उदाहरण द्वारा समझते हैं।
उदाहरण
हनुमप्पा और उसकी पत्नी गंगाम्मा गन्ने के रस से गुड़ बना रहे हैं। उन्होंने गन्ने के रस को गर्म करके राब (शीरा) बना ली है, जिसे शंकु के छिन्नक के आकार के साँचों में डाला जाता है, जिनमें से प्रत्येक के दोनों वृत्तीय फलकों के व्यास क्रमशः 30 cm और 35 cm हैं तथा साँचे की ऊर्ध्वाधर ऊँचाई 14 cm है। यदि 1 cm³ राब का द्रव्यमान लगभग 1.2 g है तो प्रत्येक साँचे में भरी जा सकने वाली राब का द्रव्यमान ज्ञात करें। (π = 22/7 लीजिए)
हल
चूँकि साँचा एक शंकु के छिन्नक के आकार का है, इसलिए इसमें भरी जा सकने वाली राब का आयतन = π/3 h(r₁² + r₂² + r₁r₂)
जहाँ r₁ बड़े आधार की त्रिज्या है और r₂ छोटे आधार की त्रिज्या है।
= 1/3 × 22/7 × 14[(35/2)² + (30/2)² + (35/2 × 30/2)] cm³ = 11641.7 cm³
यह दिया है कि 1 cm³ राब का द्रव्यमान 1.2 g है। अतः प्रत्येक साँचे में भरी जा सकने वाली राब का भार द्रव्यमान = (11641.7 × 1.2) g
= 13970.04g = 13.97 kg = 14 kg (लगभग)
उदाहरण
धातु से बनी एक खुली बाल्टी शंकु के एक छिन्नक के आकार की है, जो उसी धातु के बने एक खोखले बेलनाकार आधार पर आरोपित है (देखिए आकृति 13-23)। इस बाल्टी के दोनों वृत्ताकार सिरों के व्यास 45 cm और 25 cm हैं तथा बाल्टी की कुल ऊर्ध्वाधर ऊँचाई 40 cm और बेलनाकार आधार की ऊँचाई 6 cm है। इस बाल्टी को बनाने में प्रयुक्त धातु की चादर का क्षेत्रफल ज्ञात कीजिए जबकि हम बाल्टी की मुठिया (या हत्थे) को इसमें सम्मिलित नहीं कर रहे हैं। साथ ही, उस पानी का आयतन ज्ञात कीजिए जो इस बाल्टी में धारण कर सकता है। (π = 22/7 लीजिए)
हल
बाल्टी की कुल ऊँचाई = 40 cm है, जिसमें आधार की ऊँचाई भी सम्मिलित है। इसलिए शंकु के छिन्नक की ऊँचाई (40 – 6) cm = 34 cm है।
अतः, शंकु के छिन्नक की तिर्यक ऊँचाई l = √{h² + (r₁- r₂)²}
जहाँ r₁ = 22.5 cm, r₂ = 12.5 cm और h = 34 cm
अतः l = √{34² + (22.5 – 12.5)²}
= √{34² + 10²} = 35.44 cm
इसमें प्रयुक्त धातु की चादर का क्षेत्रफल = शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल + वृत्तीय आधार का क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल
= [π × 35.44 (22.5 + 12.5) + π × (12.5)² + 2 π × 12.5 × 6] cm²
= 22/7 × [1240.4 + 156.25 + 150] cm²
= 4860.9 cm²
अब, बाल्टी में आ सकने वाले पानी का आयतन, जिसे बाल्टी की धारिता भी कहते हैं
= (π × h)/3 (r₁² + r₂² + r₁r₂)
= 22/7 × 34/3 × [(22.5)² + (12.5)² + 22.5 × 12.5]
= 22/7 × 34/3 × 943.75 cm³ = 33615.48 cm³
= 33.62 लीटर (लगभग)
शंकु के छिन्नक का वक्र पृष्ठ का क्षेत्रफल
किसी शंकु के छिन्नक के वक्र पृष्ठ का क्षेत्रफल निम्न सूत्र से ज्ञात किया जा सकता है:
छिन्नक का वक्र पृष्ठ का क्षेत्रफल = πl(r₁+ r₂), जहाँ l तिर्यक ऊँचाई है. जहाँ l छिन्नक की तिर्यक लम्बाई है r₁ बड़े आधार वाले भाग की त्रिज्या है जबकि r₂ छोटे आधार की त्रिज्या है।
शंकु के छिन्नक का आयतन
शंकु के छिन्नक का आयतन निम्नलिखित सूत्र से ज्ञात कर सकते हैं:
= π/3 h(r₁² + r₂² + r₁r₂)
जहाँ h छिन्नक की ऊंचाई है r₁ बड़े आधार की त्रिज्या है तथा r₂ छोटे आधार की त्रिज्या है।
उदाहरण
एक शंकु के छिन्नक, जो 45 cm ऊँचा है, के सिरों की त्रिज्याएँ 28 cm और 7 cm हैं। इसका आयतन, वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 22/7 लीजिए)
हल:
इस छिन्नक को दो लंब वृत्तीय शंकुओं OAB और OCD के अंतर के रूप में देखा जा सकता है।
मान लीजिए सेंटीमीटर में शंकु OAB की ऊँचाई h₁ है और तिर्यक ऊँचाई l₁ है, अर्थात् OP = h₁ और OA = OB = l₁ है।
मान लीजिए शंकु OCD की सेंटीमीटर में ऊँचाई h₂ और तिर्यक ऊंचाई l₂ है।
हमें r₁ = 28 cm, r₂ = 7 cm और छिन्नक की ऊँचाई h = 45 cm है।
साथ ही h₁ = 45 + h₂ (1)
सबसे पहले हमें क्रमशः शंकुओं OAB और OCD की ऊँचाइयों h₁ और h₂ को निर्धारित करना आवश्यक है।
चूँकि त्रिभुज OPB और OQD समरूप हैं (क्यों?), इसलिए हमें प्राप्त है:
h₁/ h₂ = 28/7 = 4/1 (2)
(1) और (2) से हमें h₂ = 15 और h₁ = 60 प्राप्त होता है
अब, छिन्नक का आयतन = शंकु OAB का आयतन – शंकु OCD का आयतन
= [1/3 × 22/7 × (28)² × 60 – 1/3 × 22/7 × (7)² × 15] cm³ = 48510 cm³
शंकु OAB तथा शंकु OCD की तिर्यक ऊँचाइयाँ क्रमशः l₁ और l₂ नीचे दर्शाए अनुसार प्राप्त होती हैं:
l₂ = √{(7)² + (15)²} = 16.55 cm
l₁ = √{(28)² + (60)²} = 66.20 cm
इस प्रकार छिन्नक का वक्र पृष्ठीय क्षेत्रफल = π r₁ l₁ – π r₂l₂
= 22/7 × 28 × 66.20 – 22/7 × 7 × 16.55 = 54.61 cm²
अब, छिन्नक का संपूर्ण पृष्ठीय क्षेत्रफल = वक्र पृष्ठीय क्षेत्रफल + π r₁² + π r₂²
= 5461.5 cm² + 22/7 (28)² cm² + 22/7 (7)² cm²
= = 5461.5 cm² + 2464 cm² + 154 cm² = 8079.5 cm²
स्मरणीय तथ्य
- आधारभूत ठोसों घनाभ, बेलन, शंकु और गोले और अर्धगोले में से किन्हीं दो ठोसों के संयोजन (को मिलाने से) से बने ठोसों के पृष्ठीय क्षेत्रफल निर्धारित करना।
- ठोसों घनाभ, बेलन, शंकु, गोले और अर्धगोले में से किन्हीं दो ठोसों के संयोजन से बने ठोसों के आयतन ज्ञात करना।
- जब किसी शंकु को उसके आधार के समांतर किसी तल द्वारा काटकर एक छोटा शंकु हटा देते हैं, तो जो ठोस बचता है, वह शंकु का एक छिन्नक कहलाता है।
- दो घनों, जिनमे से प्रत्येक का आयतन 64 cm3 है, के सलंग्न फलकों को मिलाकर एक ठोस बनाया जाता है | इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
हल:
एक घन का आयतन = 64 cm3
एक किनारा = (64)1/3
= 4 cm
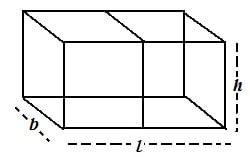
दो घनों के फलकों को मिलाने पर
l = 4 + 4 = 8 cm
b = 4 cm
h = 4 cm
इसप्रकार इस घनाभ का पृष्ठीय क्षेत्रफल = 2(lb + bh + lh)
= 2(8×4 + 4×4 + 8×4)
= 2(32 + 16 + 32)
= 2×80
= 160 cm2
अत: इस घनाभ का प्राप्त पृष्ठीय क्षेत्रफल 160 cm2 है |
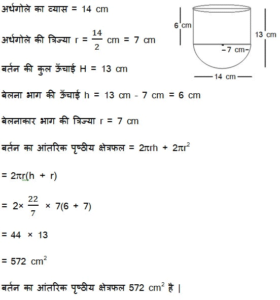
कोई बर्तन एक खोखले अर्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है | अर्धगोले का व्यास 14 cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13 cm है | इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
हल :
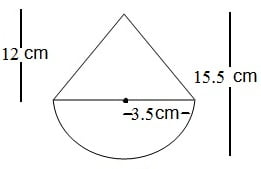
एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्ध गोले पर अध्यारोपित है | इस खिलौने की संपूर्ण ऊँचाई 15.5 cm है | इस खिलोने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
हल:
अर्धगोलाकार भाग की त्रिज्या r = 3.5 cm
शंक्वाकार भाग की त्रिज्या r = 3.5 cm
शंक्वाकार भाग की ऊँचाई h = 15.5 – 3.5 = 12 cm

भुजा 7 cm वाले एक घनाकार ब्लाक के ऊपर एक अर्धगोला रखा हुआ है | अर्धगोले का अधिकतम व्यास क्या हो सकता है ? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
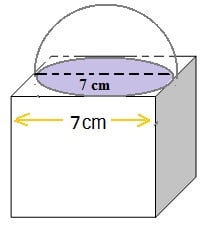
हल :
घनाकार ब्लॉक का एक किनारा = 7 cm
अर्धगोले का अधिकतम व्यास d = 7 cm
![]()
ठोस का पृष्ठीय क्षेत्रफल = घनाकार ब्लॉक का क्षेत्रफल + अर्धगोले का क्षेत्रफल – अर्धगोले से ढके एक वृत्त का क्षेत्रफल
⇒ ठोस का पृष्ठीय क्षेत्रफल = 6a2 + 2πr2 – πr2
= 6a2 + πr2 [ a = घन का एक किनारा ]

घनाकार ब्लाक के एक फलक को अन्दर की ओर से काट कर एक अर्धगोलाकार गड्ढा इस प्रकार बनाया गया है की अर्धगोले का व्यास घन के एक किनारे के बराबर है | शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
हल :
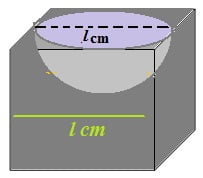

( चूँकि घन का किनारा अर्धगोले के ब्यास के बराबर है )
शेष बचे ठोस का पृष्ठीय क्षेत्रफल = घनाकार ब्लॉक का क्षेत्रफल + अर्धगोले का क्षेत्रफल – अर्धगोले से ढके एक वृत्त का क्षेत्रफल
= 6a2 + 2πr2 – πr2 [ a = घन का एक किनारा ]
= 6a2 + πr2
दवा का एक कैप्सूल (capsule) एक बेलन के आकार का है जिसके दोनों सिरों पर एक – एक अर्धगोला लगा हुआ है (देखिए आकृति 13.10) | पुरे कैप्सूल की लंबाई 14 mm है और उसका व्यास 5 mm है इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
हल:
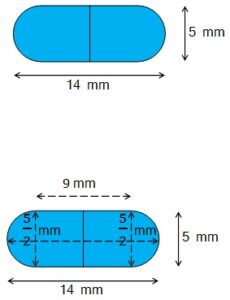
यहाँ बेलन का ब्यास, अर्धगोले के ब्यास के बराबर है |
अत: अर्धगोले का ब्यास D = 5 mm

कैप्सूल का पृष्ठीय क्षेत्रफल = 2 (अर्धगोलों का वक्र पृष्ठीय क्षेत्रफल) + बेलन का वक्र पृष्ठीय क्षेत्रफल
= 2 × 2πr2 + 2πrh
= 2πr(2r + h)

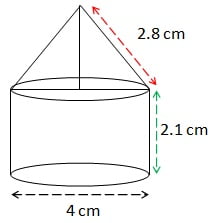
कोई तंबू एक बेलन के आकार का है जिस पर एक शंकु आध्यारोपित है | यदि बेलनाकार भाग की ऊँचाई और क्रमशः 2.1 m और 4 m है तथा शंकु की तिर्यक ऊँचाई 2.8 m है तो इस तंबू को बनाने में प्रयुक्त कैनवस (canvas) का क्षेत्रफल ज्ञात कीजिए | साथ ही, 500 रू प्रति m2 की दर से इसमें प्रयुक्त कैनवस की लागत ज्ञात कीजिए | (ध्यान दीजिए कि तंबू के आधार को कैनवस से नहीं ढका जाता है |)
हल :
तम्बू के बेलनाकार भाग का ब्यास = 4 cm
अत: त्रिज्या r = 2 cm
बेलनाकार भाग की ऊँचाई h = 2.1 cm
शंकु की तिर्यक ऊँचाई l = 2.8 cm
ब्यास = 4 cm
और त्रिज्या r = 2 cm
इस तंबू को बनाने में प्रयुक्त कैनवस (canvas) का क्षेत्रफल
= बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल + शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
= 2πrh + πrl

ऊँचाई 2.4 cm और व्यास 1.4 cm वाले एक ठोस बेलन में से ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (cavity) काट लिया जाता है |शेष बचे ठोस का निकटतम वर्ग सेंटीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
हल :
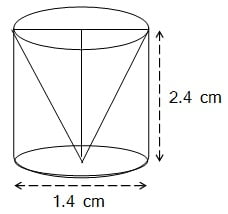
बेलन की ऊँचाई h = 2.4 cm
बेलन का ब्यास = 1.4 cm
अत: बेलन की त्रिज्या r = 0.7 cm
काटे गए शंकु की ऊँचाई h = 2.4 cm
और त्रिज्या r = 0.7 cm
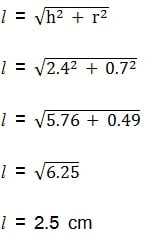
शेष बचे ठोस का पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + शंकु का वक्र पृष्ठीय क्षेत्रफल + बेलन के पेंदी का क्षेत्रफल
= 2πrh + πrl + πr2
= πr(2h + l + r)
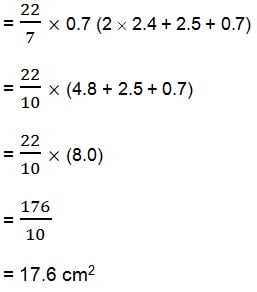
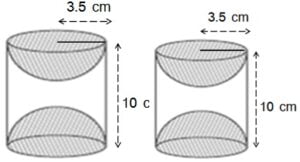
लकड़ी के ठोस बेलन के प्रत्येक सिरे पर एक अर्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसाकि आकृति 13.11 में दर्शाया गया है | यदि बेलन की ऊँचाई 10 cm है और आधार की त्रिज्या 3.5 cm है तो इस वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए |
हल :
बेलन की ऊँचाई = 10 cm
आधार की त्रिज्या = 3.5 cm
अर्धगोले की त्रिज्या = 3.5 cm
वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल
= बेलन का वक्र पृष्ठीय क्षेत्रफल + उपरी अर्धगोले का वक्र पृष्ठीय क्षेत्रफल + निचली अर्धगोले का वक्र पृष्ठीय क्षेत्रफल
= 2πrh + 2πr2 + 2πr2
= 2πr(h + r + r )
= 2πr(h + 2r )
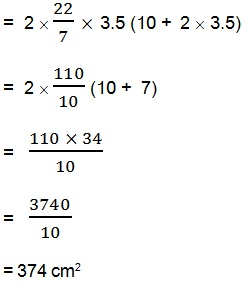
एक ठोस एक अर्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 cm हैं तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है | इस ठोस का आयतन π के पदों में ज्ञात कीजिए |
हल :

एक इंजीनियरिंग के विधार्थी रचेल से एक पतली एल्युमिनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया जो एक ऐसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों | इसा मॉडल का व्यास 3 cm है और इसकी लंबाई 12 cm है | यदि प्रत्येक शंकु की ऊँचाई 2 cm हो तो रचेल द्वारा बनाए गए मॉडल में अंतर्विष्ट हवा का आयतन ज्ञात कीजिए|
(यह मान लीजिए कि मॉडल की आंतरिक और बाहरी विमाएँ लगभग बराबर है |)

एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है | 45 गुलाबजामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्धगोलाकार हैं तथा इसकी लंबाई 5 cm और व्यास 2.8 cm है
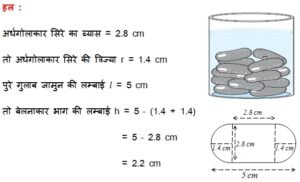
सभी 45 गुलाब जामुनों का आयतन = 45(अर्धगोले का आयतन + बेलन का आयतन + अर्धगोले का आयतन)
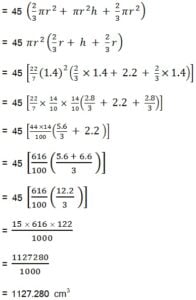

एक कमलदान घनाभ के आकार की एक लकड़ी से बना हा जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढे बने हुए हैं | घनाभ की विमाएँ 15 cm x 10 cm x 3.5 cm हैं | प्रत्येक गड्ढे की त्रिज्या 0.5 cm है और गहराई 1.4 cm है | पुरे कमलदान में लकड़ी का आयतन ज्ञात कीजिए
हल :
धनाभ की लंबाई l = 15 cm
घनाभ की चौड़ाई b = 10 cm
घनाभ की ऊँचाई h = 3.5 cm
शंक्वाकार भाग की त्रिज्या (r) = 0.5 cm
ऊँचाई (h) = 1.4 cm
पूरे कमलदान की लकड़ी का आयतन = घनाभ का आयतन – चरों शंक्वाकार गढ्ढे का आयतन

एक बर्तन एक उल्टे शंकु के आकार का है | इसकी ऊँचाई 8 cm है और इसके ऊपरी सिरे (जो खुला हुआ है ) की त्रिज्या 5 cm त्रिज्या है | यह ऊपर तक पानी से भरा हुआ है | जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमे प्रत्येक 0.5 cm त्रिज्या वाला एक गोला है, डाली जाती हैं, तो इसमें से भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है | बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए |
हल :
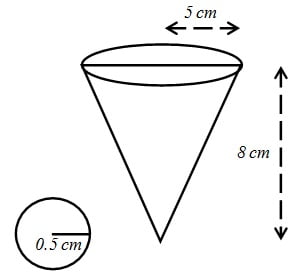
शंकु की ऊँचाई (h) = 8 cm
शंकु की त्रिज्या (R) = 5 cm
गोली की त्रिज्या (r) = 0.5 cm
माना बर्तन में डाली गई गोलियों की संख्या = n

अत: गोलियों की संख्या 100 है |
ऊँचाई 220 cm और आधार व्यास 24 cm वाले एक बेलन, जिस पर ऊँचाई 60 cm और त्रिज्या 8 cm वाला एक अन्य बेलन आरोपित है, से लोहे का स्तंभ बना है | इस स्तंभ का द्रव्यमान ज्ञात कीजिए, जबकि दिया है 1 cm3 लोहे का द्रव्यमान लगभग 8 g होता है | (π = 3.14 लीजिए |)
हल :
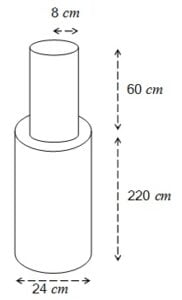
मोटे बेलन की ऊँचाई (H) = 220 cm
व्यास (d) = 24 cm
अत: त्रिज्या (R) = 12 cm
पतले बेलन की ऊँचाई (h) = 60 cm
त्रिज्या (r) = 8 cm

एक ठोस में, ऊँचाई 120 cm और त्रिज्या 60 cm वाला एक शंकु सम्मिलित है, जो 60 cm त्रिज्या वाले एक अर्धगोले पर आरोपित है | इस ठोस को पानी से भरे हुए एक लंब वृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे | यदि बेलन की त्रिज्या 60 cm है और ऊँचाई 180 cm है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए |
हल :
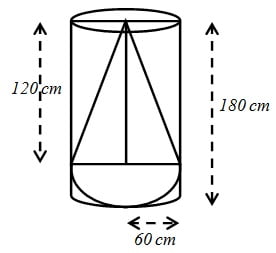
ठोस के शंकु की ऊँचाई (h) = 120 cm
ठोस के शंकु की त्रिज्या (r) = 60 cm
ठोस के अर्धगोले की त्रिज्या (r) = 60 cm
बड़े बेलन की ऊँचाई (H) = 180 cm
बड़े बेलन की की त्रिज्या (r) = 60 cm
शेष बचे पानी का आयतन = बड़े बेलन का आयतन – ठोस का आयतन
एक गोलाकार काँच के बर्तन की एक बेलन के आकार की गर्दन है जिसकी लंबाई 8 cm है और व्यास 2 cm है जबकि गोलाकार भाग का व्यास 8.5 cm है | इसमें भरे जा सकने वाली पानी की मात्रा माप कर, एक बच्चे ने यह ज्ञात किया कि इस बर्तन का आयतन 345 cm3 है | जाँच कीजिए कि बच्चे का उत्तर सही है या नहीं, यह मानते हुए की उपरोक्त मापन आंतरिक मापन है और π = 3.14 |
हल :
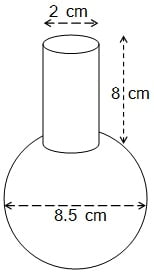

इसमें भरे जा सकने वाले पानी का आयतन = गोले का आयतन + बेलन का आयतन

त्रिज्या 4.2 cm वाले धातु के एक गोले को पिघलाकर त्रिज्या 6 cm वाले एक बेलन के रूप में ढाला जाता है | बेलन की ऊँचाई ज्ञात कीजिए |
हल :
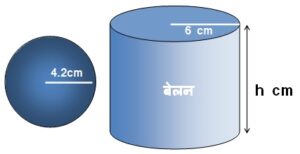
धातु के गोले की त्रिज्या (r) = 4.2 cm
बेलन की त्रिज्या (R) = 6 cm और
माना बेलन की ऊँचाई h cm है |
बेलन का आयतन = गोले का आयतन
- क्रमशः 6 cm, 8 cm और 10 cm त्रिज्याओं वाले धातु के ठोस गोलों को पिघलाकर एक बड़ा ठोस गोला बनाया जाता है | इस गोले की त्रिज्या ज्ञात कीजिए |

- व्यास 7 m वाला 20 m गहरा एक कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप से फैलाकर 22 m x 14 m वाला एक चबूतरा बनाया गया है | इस चबूतरे की ऊँचाई ज्ञात कीजिए |
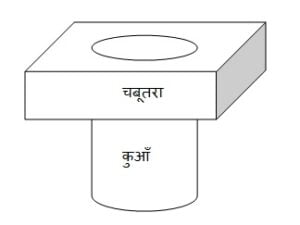

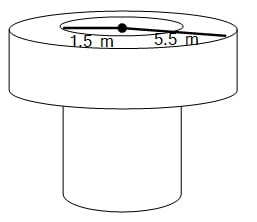
- व्यास 3 m वाला 14 m गहरा की गहराई तक खोदा जाता है | इससे निकली हुई मिट्टी को कुँए के चारों ओर 4 m चौड़ी एक वृत्ताकार वलय (ring) बनाते हुए, समान रूप से फैलाकर एक प्रकार का बाँध बनाया जाता है | इस बाँध की ऊँचाई ज्ञात कीजिए |

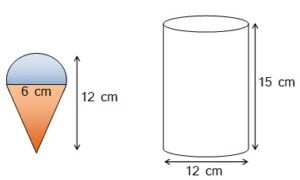
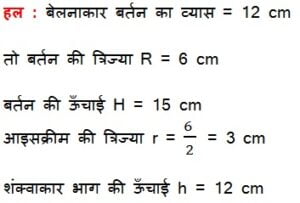
- व्यास 12 cm और ऊँचाई 15 cm वाले एक लंब वृत्तीय बेलन के आकार का बर्तन आइसक्रीम से पूरा भरा हुआ है | इस आइसक्रीम को ऊँचाई 12 cm और व्यास 6 cm वाले शकुओं में भरा जाना है, जिनका ऊपरी सिरा अर्धगोलाकार होगा | उन शंकुओं की संख्या ज्ञात कीजिए जो इस आइसक्रीम से भरे जा सकते हैं |

- विमाओं 5.5 cm x 10 cm x 3.5 cm वाला एक घनाभ बनाने के लिए, 1.75 cm व्यास और 2 mm मोटाई वाले कितने चाँदी के सिक्कों को पिघलाना पड़ेगा ?

- 32 cm ऊँची और आधार त्रिज्या 18 cm वाली एक बेलनाकार बाल्टी रेत से भरी हुई है | इस बाल्टी को भूमि पर खाली किया जाता है और इस रेते की एक शंक्वाकार ढेरी बनाई जाती है | यदि शंक्वाकार ढेरी की ऊँचाई 24 cm है, तो इस ढेरी की त्रिज्या और तिर्यक ऊँचाई ज्ञात कीजिए |

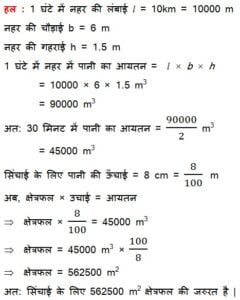
- m चौड़ी और 1.5 m गहरी एक नहर में पानी 10 km /h की चाल से बह रहा है | 30 मिनट में, यह नहर कितने क्षेत्रफल की सिंचाई कर पाएगी, जबकि सिंचाई के ल;इए 8 cm गहरे पानी की आवश्यकता होती है |
- पानी पीने वाला एक गिलास 14 cm ऊँचाई वाले एक शंकु के छिन्नक के आकार का है | दोनों वृत्ताकार सिरों के व्यास 4 cm और 2 cm हैं | इस गिलास की धारिता ज्ञात कीजिए |

- एक शंकु के छिन्नक की तिर्यक ऊँचाई 4 cm है तथा इसके वृत्तीय सिरों के परिमाप (परिधियाँ) 18 cm और 6 cm हैं | इस छिन्नक का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए |

- एक तुर्की टोपी शंकु के एक छिन्नक के आकर की है (देखिये आकृति 13.24) | यदि इसके खुले सिरे की त्रिज्या 10 cm है, ऊपरी सिरे की त्रिज्या 4 cm है टोपी की तिर्यक ऊँचाई 15 cm है तो इसके बनाने में प्रयुक्त पदार्थ का क्षेत्रफल ज्ञात कीजिए|

We hope that class 10 Math Chapter 13 पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 13 पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…