पाठ – 14
सांख्यिकी
In this post we have given the detailed notes of class 10 Math chapter 14 Statistics in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 14 सांख्यिकी के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 14 |
| Chapter Name | सांख्यिकी (Statistics) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 14 सांख्यिकी
सांख्यिकी
शाब्दिक रूप में सांख्यिकी शब्द अंग्रेजी के शब्द statistics का हिन्दी रूपान्तर है जो लैटिन भाषा के शब्द स्टेटस (status) तथा जर्मन भाषा शब्द statistik से भी जोड़ते हैं जिसका अर्थ राज्य है। साख्यिकी का शाब्दिक अर्थ है संख्या से संबंधित शास्त्र। इस प्रकार विषय के रूप में सांख्यिकी ज्ञान की वह शाखा है जिसका संबंध संख्याओं या संख्यात्मक आंकड़ों से हो। सांख्यिकी सिद्धान्तों को वैज्ञानिक रूप में प्रस्तुत करने का श्रेय जर्मन विद्वान गाॅटफ्रायड एचेनवाल को है इसी कारण एकेनवेल को सांख्यिकी का जनक कहा जाता है। वर्तमान युग में सांख्यिकी को विकसित करने में कार्ल पियर्सन का योगदान सबसे अधिक है।
सांख्यिकी की परिभाषा
- बाउले – “समंक किसी अनुसंधान के किसी विभाग में तथ्यों का संख्या के रूप में प्रस्तुतीकरण है, जिन्हें एक दूसरे से सम्बन्धित रूप में प्रस्तुत किया जाता है”।
- कानर – “सांख्यिकी किसी प्राकृतिक अथवा सामाजिक समस्या से सम्बन्धित माप की गणना या अनुमान का क्रमबद्ध एवं व्यवस्थित ढंग है जिससे कि अन्तसम्बन्धों का प्रदर्शन किया जा सके”।
- वालिस और राबटस – “सांख्यिकी के परिमाणात्मक पहलुओं के संख्यात्मक विवरण है जो मदों की गिनती या माप के रूप में व्यक्त होते हैं”।
सांख्यिकी के प्रकार
सांख्यिकी के मुख्यतः दो प्रकार प्रचलित है –
1. प्राचल सांख्यिकी
प्राचल सांख्यिकी में सभी के किसी एक विशेष प्राचल से संबंधित होता है तथा आंकड़ों के आधार पर प्राचल के संबंध में अनुमान लगाया जाता है। प्राचल सांख्यिकी में जिस प्रकार के आंकड़ों का विश्लेषण किया जाता है वह आंकड़ें न्यादर्श और सामान्य विवरण से संबंधित होते है।
2. अप्राचल सांख्यिकी
अप्राचल सांख्यिकी को वितरण मुक्त सांख्यिकी भी कहा जाता है क्योंकि कुछ आंकड़ें ऐसे भी होते है जहां न तो संयोगिक चयन होता है और न सामान्य वितरण हो। ऐसे आंकड़ों की संख्या कम होने के कारण आकड़ों का स्वरूप रूप बिगड़ा हुआ होता है और इनका एक समग्र के प्राचल से संबंध नहीं होता है। ऐसे आंकडों से संबंधित सांख्यिकी विधियां अप्राचल सांख्यिकी में आती हैं। माध्यिका, सहसंबंध, काई टेस्ट, माध्यिका टेस्ट ये प्रमुख सांख्यिकी विधियां है।
व्यावहारिक सांख्यिकी के मुख्यतः दो प्रकारों में बाट कर सकते है।
- वर्णनात्मक सांख्यिकी
- अनुमानिक सांख्यिकी
वर्णनात्मक सांख्यिकी – वर्णनात्मक सांख्यिकी में वे विधियां आती है जिनके प्रयोग से किसी न्यादर्श की विशेषताओं का प्राप्त आंकडों के आधार पर वर्णन किया जाता है। इस प्रकार की सांख्यिकी का प्रयोग सांख्यिकी में प्रदत्तों का संकलन, संगठन, प्रस्तुतीकरण एवं परिकलन से होता हैं इसके अंतर्गत प्रदत्तों का संकलन करके सारणीबद्ध किया जाता है और प्रदत्तों की विशेषता स्पष्ट करने के लिए कुछ सरल सांख्यिकीय मानों की गणना की जाती है- जैसे केन्द्रीय प्रवृत्ति के मापकों, विचलन मापकों तथा सहसंबंध आदि का प्रयोग वर्ग की प्रकृति तथा स्थिति आदि जानने के लिए किया जाता है।
अनुमानिक सांख्यिकी – अनुमानिक सांख्यिकी विधियां का प्रयोग किसी जनसंख्या से लिये गए न्यादर्श के विशेष में तथ्य एकत्र करके उसके आधार पर जनसंख्या के विषय में निष्कर्ष निकालने के लिए किया जाता है। बहुधा इस सांख्यिकी की सहायता से परिणामों की वैधता जांच की जाती है। बहुधा अनुमान के लिए अपेक्षाकृत उच्च सांख्यिकी विधियों का प्रयोग किया जाता है जैसे सम्भावना नियम, मानक त्रुटि, सार्थकता, परीक्षण आदि। चूंकि समूह विस्तृत होते है तथा इनके सदस्यों की संख्या अधिक होती है अतः अध्ययनकत्र्ता अध्ययन के लिए इन बड़े समूहों से न्यादर्श को चुनकर समस्या का अध्ययन से प्राप्त निष्कर्ष सम्पूर्ण समूह का प्रतिनिधित्व करते है।
सांख्यिकी की विशेषताएं
- तथ्यों के किसी समूह अथवा उस पर आधारित निष्कर्ष को सांख्यिकी कहा जाता है। उदाहरण- किसी एक व्यक्ति की महीने की आय सांख्यिकी नहीं है बल्कि बहुत से लोगों की महीने की आय से प्राप्त औसत आय को सांख्यिकी आँकड़ा कहा जाता है।
- सांख्यिकी उपयोग किसी तथ्य की गुणात्मक महत्व अर्थात अच्छा, बुरा, उचित अथवा अनुचित को व्यक्त नहीं करता है। इसके विपरीत प्रत्येक निष्कर्ष को प्रतिशत, अनुपात, औसत अथवा विचलन के रूप में संख्या के द्वारा व्यक्त किया जाता है। वास्तविक अर्थो में सांख्यिकी संख्यात्मक आँकड़ों का समूह होता है। किसी उद्योग क्षेत्र के प्रबन्धक का वेतन श्रमिकों से ज्यादा होता है, इस तथ्य द्वारा सांख्यिकी प्रकृति प्रदर्शित नहीं होती है, जबकि विभिन्न श्रेणियों के कार्मिकों की औसत मासिक आय की परस्पर तुलना तथ्यों को सांख्यिकी रूप में प्रस्तुत करेगी।
- सांख्यिकी में आँकड़ों समंको का संकलन एक पूर्व निश्चित उद्देश्य को दृष्टिगत रखकर किया जाता है। सांख्यिकीय समंक यत्र-तत्र अव्यवस्थित नहीं होते लेकिन यह अति व्यवस्थित एवं योजनाबद्ध रूप में होते हैं। किसी पूर्व निर्धारित उद्देश्य की अनुपस्थिति में प्राप्त किये जाने वाले तथ्यों को संख्या कहा जा सकता है लेकिन वह आँकड़ों की श्रेणी में नहीं आते है।। जैसे किसी औद्योगिक क्षेत्र में श्रमिकों की सामाजिक आर्थिक स्थिति का अध्ययन किया जाना है तो पहले में ही उद्देश्य निर्धारित किया जाता है कि तथ्यों का संग्रहीकरण किस लक्ष्य के लिए किया जा रहा है। इस लक्ष्य के लिए कार्य घण्टे, दैनिक मजदूरी , स्वास्थ्य दशाएं, परिवार का आकार, शैक्षणिक स्तर आदि तथ्य एकत्र किये जा सकते है।
- सांख्यिकी का संबंध उन आँकड़ों से भी होता है जो एक दूसरे के साथ तुलना योग्य होते है। तुलनात्मक अध्ययन के लिए तुलना की श्रेणियों में सजातीय एकरूपता का होना अनिवार्य है। उदाहरण के लिए यदि व्यक्तियों की आय की तुलना वृक्षारोपण के आँकड़ों से की जायेगी तो समरूपता न होने का कारण उन्हें सांख्यिकी मे नहीं रखा जा सकता है। उक्त उदाहरण से स्पष्ट होता हे कि आँकड़ों के केवल उन समूहों को सांख्यिकी कहा जा सकता है जो परस्पर तुलना योग्य हों।
- आँकड़ों में पर्याप्त शुद्धता की उपस्थिति सांख्यिकी की एक विशेष आवश्यकता होती है। इसका आशय यह है कि अध्ययन विषय की प्रकृति तथा अनुसंधान का उद्देश्य शुद्ध होना चाहिए। आँकड़ों की शुद्धता का संबंध विषय की प्रकृति एवं विशिष्ट परिस्थिति से होता है। इस परिशुद्धता का निर्धारण संमको की मात्रा अथवा संख्या से किया जाता है जिसके आधार पर एक उपयोगी निष्कर्ष निरूपित किया जा सकता है।
- सांख्यिकी की इस विशेष के तहत तथ्यों का संकलन योजनापूर्ण तरीके से किया जाता है क्योंकि अव्यवस्थित आँकड़े किसी भी निष्कर्ष को वस्तुनिष्ठतापूर्वक निरूपित नहीं कर सकते हैं।
- यह मालूम है कि विज्ञान होने के कारण सांख्यिकी से संबंधित आँकड़े अनेक कारणों अथवा कारकों से प्रभावित होते है। सांख्यिकी का संबंध किसी एक पक्ष मात्र के विष्लेशण से ही नहीं बल्कि उन सभी कारकों के आंकलन अथवा विवेचन से भी होता है जो किसी विशेष दशा में परिवर्तन उत्पन्न करते हैं, साथ ही घटनाओं के मध्य परस्पर सह-संबंध को व्यक्त करते हैं।
- सांख्यिकी मे निहित आँकड़ों का संकलन कई पद्धतियों एवं तकनीक पर आधारित होते है। उद्देश्यपूर्ण विधि से संकलित संगणना व निदर्शन आधारित आँकड़े सांख्यिकी की विशेषता को स्पष्ट करते हैं। सीमित अनुसंधान क्षेत्र में संमको का एकत्रीकरण संगणना विधि तथा विस्तृत अनुसंधान क्षेत्र में आँकड़ों का संकलन निदर्शन अर्थात् संबधित पूर्ण इकाइयों में से कुछ प्रतिनिधि इकाइयों का चयन करके किया जाता है।
- विशेष रूप से सांख्यिकी एक ऐसा विज्ञान है जो आँकड़ों के आधार पर किसी विषय से संबंधित सामान्य प्रवृत्तियों को स्पष्ट करता है। सांख्यिकी की आधारभूत मान्यता यह है कि कतिपय संख्याओं के आधार पर निरूपित निष्कर्ष दूसरी संख्याओं पर लागू होता है। जैसे- यदि किसी विशेष समाज में कार्यदशाओं, स्वास्थ्य- स्तर, मासिक आय, जन्म दर, मृत्यु दर आदि आँकड़े एकत्रित कर लिये जाये तो उनके आधार पर उसी प्रकार के अन्य समाजों के लिए भी जनसंख्या संबंधी सामानय प्रवृत्तियों को समझा जा सकता है।
वर्गीकृत आंकड़े
अपरिष्कृत आँकड़ों को वर्गीकृत करने का उद्देश्य उन्हें व्यवस्थित करना है, ताकि उन्हें आसानी से आगे के सांख्यिकीय विशलेषण के योग्य बनाया जा सके। समूह या वर्ग बन जाता है।
वर्गीकृत आँकड़ों का माध्य
यदि प्रेक्षणों x₁, x₂, ……….., xₙ की बारंबारताएँ क्रमशः f₁, f₂, ……….., fₙ हों, तो इसका अर्थ है कि प्रेक्षण x₁, f₁ बार आता है प्रेक्षण x₂, f₂ बार आता है, इत्यादि।
अब, सभी प्रेक्षणों के मानों का योग = f₁x₁ + f₂x₂ + ……….. + fₙxₙ है तथा प्रेक्षणों की संख्या f₁ + f₂ + ……….., + fₙ है।
अतः, इनका माध्य x निम्नलिखित द्वारा प्राप्त होगा:
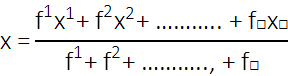
या माध्य 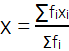
इसे और अधिक संक्षिप्त रूप में, 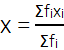
लिखते हैं, यह समझते हुए कि i का मान 1 से n तक विचरण करता है।
हल
अब, माध्य 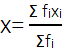
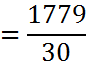
वर्ग अंतराल
उदाहरण 1 के अवर्गीकृत आँकड़ों को चौड़ाई, मान लीजिए, 15 के वर्ग अंतराल बनाकर वर्गीकृत आँकड़ों में बदलें। याद रखिए कि वर्ग अंतरालों की बारंबारताएँ निर्दिष्ट करते समय, किसी उपरि वर्ग सीमा में आने वाले प्रेक्षण अगले वर्ग अंतराल में लिए जाते हैं। उदाहरणार्थ, अंक 40 प्राप्त करने वाले 4 विद्यार्थियों को वर्ग अंतराल 25-40 में न लेकर अंतराल 40-55 में लिया जाता है। इस परंपरा को ध्यान में रखते हुए, आइए इनकी एक वर्गीकृत बारंबारता सारणी बनाएँ:
वर्ग अंतराल | विद्यार्थियों की संख्या |
10-25 | 2 |
25-40 | 3 |
40-55 | 7 |
55-70 | 6 |
70-85 | 6 |
85-100 | 6 |
मध्य बिंदु
अब, प्रत्येक वर्ग अंतराल के लिए, हमें एक ऐसे बिदु (मान) की आवश्यकता है, जो पूरे अंतराल का प्रतिनिधित्व करे। यह मान लिया जाता है कि प्रत्येक वर्ग अंतराल की बारंबारता उसके मध्य-बिदु के चारों ओर केंद्रित होती है। अतः, प्रत्येक वर्ग के मध्य-बिंदु या वर्ग चिह्न को उस वर्ग में आने वाले सभी प्रेक्षणों का प्रतिनिधि माना जा सकता है। याद कीजिए कि हम एक वर्ग अंतराल का मध्य बिदु (या वर्ग चिह्न) उसकी उपरि और निचली सीमाओं का औसत निकालकर ज्ञात करते हैं। अर्थात्
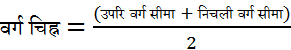
उदाहरण के लिए वर्ग 10 – 25 के लिए वर्ग चिह्न ![]() है । इसी प्रकार अन्य वर्गों के लिए वर्ग चिह्न प्राप्त कर सकते हैं।
है । इसी प्रकार अन्य वर्गों के लिए वर्ग चिह्न प्राप्त कर सकते हैं।
इससे हमें प्रत्येक वर्ग के लिए fᵢxᵢ प्राप्त हो जायेगा।
अतः, दिए हुए आँकड़ों का माध्य x, नीचे दर्शाए अनुसार प्राप्त होता हैः
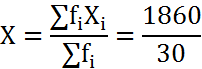
= 62
नोट: माध्य ज्ञात करने की इस नयी विधि को प्रत्यक्ष विधि कहा जा सकता है।
कल्पित माध्य
कभी-कभी जब xᵢ और fᵢ के मान बड़े होते हैं, तो xᵢ और fᵢ के गुणनफल ज्ञात करना जटिल हो जाता है तथा इसमें समय भी अधिक लगता है। अतः, ऐसी स्थितियों के लिए, आइए इन परिकलनों को सरल बनाने कल्पित माध्य विधि का सहारा लेते हैं। हम fᵢ के साथ कुछ नहीं कर सकते, परंतु हम प्रत्येक xᵢ को एक छोटी संख्या में बदल सकते हैं, जिससे हमारे परिकलन सरल हो जाएँगे।
इसमें पहला चरण यह हो सकता है कि प्राप्त किए गए सभी xᵢ में से किसी xᵢ को कल्पित माध्य के रूप में चुन लें तथा इसे “a” से व्यक्त करें। साथ ही, अपने परिकलन कार्य को और अधिक कम करने के लिए, हम “a” को ऐसा xᵢ ले सकते हैं जो x₁, x₂, ……….., xₙ के मध्य में कहीं आता हो। अतः, हम a = 47.5 या a = 62.5 चुन सकते हैं। आइए a = 47.5 चुनें।
अगला चरण है कि a और प्रत्येक xᵢ के बीच का अंतर dᵢ ज्ञात किया जाए, अर्थात् प्रत्येक xᵢ से “a” का विचलन ज्ञात किया जाए।
अर्थात् dᵢ = xᵢ – a
तीसरा चरण है कि प्रत्येक dᵢ और उसके संगत fᵢ का गुणनफल ज्ञात करके सभी fᵢ dᵢ का योग ज्ञात किया जाए।
विचलनों का माध्य 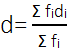
या माध्य 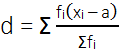
अर्थात् 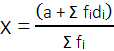
नोट: माध्य ज्ञात करने की उपरोक्त विधि कल्पित माध्य विधि कहलाती है।
वर्गीकृत आंकड़ों का बहुलक
बहुलक दिए हुए प्रेक्षणों में वह मान है जो सबसे अधिक बार आता है, अर्थात् उस प्रेक्षण का मान जिसकी बारंबारता अधिकतम है।
उदाहरण:
किसी गेंदबाज़ द्वारा 10 क्रिकेट मैचों में लिए गए विकिटों की संख्याएँ निम्नलिखित हैं: 2, 6, 4, 5, 0, 2, 1, 3, 2, 3
इन आँकड़ों का बहुलक ज्ञात कीजिए।
हल
आइए उपरोक्त आँकड़ों के लिए, एक बारंबारता बंटन सारणी बनाएँ, जैसा कि नीचे दर्शाया गया है:
विकेटों की संख्या | क्रिकेट मैचों की संख्या |
0 | 1 |
1 | 1 |
2 | 3 |
3 | 2 |
4 | 1 |
5 | 1 |
6 | 1 |
स्पष्ट है कि गेंदबाज़ ने अधिकतम मैचों (3) में 2 विकिट लिए हैं। अतः, इन आँकड़ों का बहुलक 2 है।
बहुलक वर्ग
एक वर्गीकृत बारंबारता बंटन में, बारंबारताओं को देखकर बहुलक ज्ञात करना संभव नहीं है। यहाँ, हम केवल वह वर्ग ज्ञात कर सकते हैं जिसकी बारंबारता अधिकतम है। इस वर्ग को बहुलक वर्ग कहते हैं। बहुलक इस बहुलक वर्ग के अंदर कोई मान है, जिसे निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है:
बहुलक 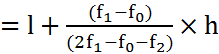
जहाँ l = बहुलक वर्ग की निम्न (निचली) सीमा
h = वर्ग अंतराल की माप (यह मानते हुए कि सभी अंतराल बराबर मापों के हैं)
f₁ = बहुलक वर्ग की बारंबारता
f₀ = बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता तथा
f₂ = बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता है।
उदाहरण:
विद्यार्थियों के एक समूह द्वारा एक मोहल्ले के 20 परिवारों पर किए गए सर्वेक्षण के परिणामस्वरूप विभिन्न परिवारों के सदस्यों की संख्या से संबंधित निम्नलिखित आँकड़े प्राप्त हुए:
परिवार माप | परिवारों की संख्या |
1-3 | 7 |
3-5 | 8 |
5-7 | 2 |
7-9 | 2 |
9-11 | 1 |
इन आँकड़ों का बहुलक ज्ञात कीजिए।
हल
यहाँ, अधिकतम वर्ग बारंबारता 8 है तथा इस बारंबारता का संगत वर्ग 3-5 है। अतः, बहुलक वर्ग 3-5 है।
अब, बहुलक वर्ग = 3 – 5, बहुलक वर्ग की निम्न सीमा (l) = 3 तथा वर्ग माप (h) = 2 है।
बहुलक वर्ग की बारंबारता (f₁) = 8
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f₀) = 7 तथा
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f₂) = 2 है।
आइए इन मानों को सूत्र में प्रतिस्थापित करें। हमें प्राप्त होता है:
बहुलक 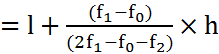
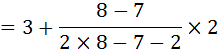
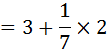
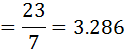
अतः, उपरोक्त आँकड़ों का बहुलक 3.286 है।
वर्गीकृत आँकड़ों का माध्यक
माध्यक (उमकपंद) केंद्रीय प्रवृत्ति का ऐसा मापक है, जो आँकड़ों में सबसे बीच के प्रेक्षण का मान देता है। अवर्गीकृत आँकड़ों का माध्यक ज्ञात करने के लिए, पहले हम प्रेक्षणों के मानों को आरोही क्रम में व्यवस्थित करते हैं। अब, यदि n विषम है, तो माध्यक (n + 1)/2 वें प्रेक्षण का मान होता है। यदि n सम है, तो माध्यक n वें और n/2 + 1 वें प्रेक्षणों के मानों का औसत (माध्य) होता है।
संचयी बारंबारता
वर्गीकृत आँकड़ों का माध्य ज्ञात करने के लिए, यह कल्पना की जाती है कि प्रत्येक वर्ग अंतराल की बारंबारता उसके मध्य-बिंदु पर केंद्रित होती है। माध्य (x) = , जहाँ x, (वर्ग चिह्न) n वें वर्ग अंतराल का मध्य-बिंदु है तथा f उसकी संगत बारंबारता है।
माध्यक वर्ग
इस अंतराल को ज्ञात करने के लिए, हम सभी वर्गों की संचयी बारंबारताएँ और n/2 ज्ञात करते हैं। अब, हम वह वर्ग खोजते हैं जिसकी संचयी बारंबारता n/2 से अधिक और उसके निकटतम है। इस वर्ग को माध्यक वर्ग कहते हैं।
माध्यक वर्ग ज्ञात करने के बाद, हम निम्नलिखित सूत्र का प्रयोग करके माध्यक ज्ञात करते हैं:
माध्यक = l + (n/2 – cf)/f × h
जहाँ l = माध्यक वर्ग की निम्न सीमा
n = प्रेक्षणों की संख्या
cf = माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता
f = माध्यक वर्ग की बारंबारता
h = वर्ग माप (यह मानते हुए कि वर्ग माप बराबर हैं)
माध्यक का उदाहरण
1. किसी स्कूल की कक्षा ग् की 51 लड़कियों की ऊँचाइयों का एक सर्वेक्षण किया गया और निम्नलिखित आँकड़े प्राप्त किए गए:
ऊंचाई (cm) में लड़कियों की संख्या
- 140 से कम 4
- 145 से कम 11
- 150 से कम 29
- 155 से कम 40
- 160 से कम 46
- 165 से कम 51
माध्यक ऊँचाई ज्ञात कीजिए।
हल
माध्यक ऊँचाई ज्ञात करने के लिए, हमें वर्ग अंतराल और उनकी बारंबारताओं की आवश्यकता है। चूँकि दिया हुआ बंटन कम प्रकार का है, इसलिए हमें वर्ग अंतरालों की उपरि सीमाएँ 140, 145, 150, ………., 165 प्राप्त होती हैं तथा इनके संगत वर्ग अंतराल क्रमशः 140 से कम, 140-145, 145-150, ………, 160-165 हैं। दिए हुए बंटन से, हम देखते हैं कि ऐसी 4 लड़कियाँ हैं जिनकी ऊँचाई 140 से कम है, अर्थात् वर्ग अंतराल 140 से कम की बारंबारता 4 है। अब 145 cm से कम ऊँचाई वाली 11 लड़कियाँ हैं और 140 cm से कम ऊँचाई वाली 4 लड़कियाँ हैं। अतः, अंतराल 140 – 145 में ऊँचाई रखने वाली लड़कियों की संख्या 11 – 4 = 7 होगी। अर्थात् वर्ग अंतराल 140 – 145 की बारंबारता 7 है। इसी प्रकार, 145 – 150 की बारंबारता 29 – 11 = 18 है, 150 – 155 की बारंबारता 40 – 29 = 11 है, इत्यादि। अतः संचयी बारंबारताओं के साथ हमारी बारंबारता बंटन सारणी निम्नलिखित रूप की हो जाती है:
वर्ग अंतराल बारंबारता संचयी बारंबारता
- 140 से कम 4 4
- 140 – 145 7 11
- 145 -150 18 29
- 150 – 155 11 40
- 155 – 160 6 46
- 160 – 165 5 51
अब n = 51 है। अतः, n/2 = 51/2 = 25.5 है। यह प्रेक्षण अंतराल 145 – 150 में आता है। तब, l (निम्न सीमा) = 145, माध्यक वर्ग 145 – 150 के ठीक पहले वर्ग की संचयी बारंबारता (cf ) = 11,
माध्यक वर्ग 145 – 150 की बारंबारता f = 18 तथा वर्ग माप h = 5 है।
सूत्र, माध्यक = l + (n/2 – cf)/f × h का प्रयोग करने पर, हमें प्राप्त होता है:
माध्यक = 145 + (25.5 – 11)/18 × 5
= 145 + 72.5/18 = 149.03
अतः, लड़कियों की माध्यक ऊँचाई 149.03 cm है।
इसका अर्थ है कि लगभग 50% लड़कियों की ऊँचाइयाँ 149.03 cm से कम या उसके बराबर है तथा शेष 50% की ऊँचाइयाँ 149.03 cm से अधिक है।
2. विधार्थियों के एक समूह द्वारा अपने पर्यावरण संचेतना अभियान के अन्तर्गत एक सर्वेक्षण किया गया, जिसमें उन्होंने एक मोहल्ले के 20 घरों में लगे हुए पौधों से संबंधित निम्नलिखित आँकड़े एकत्रित किए | प्रति घर पौधों की संख्या ज्ञात कीजिए |

माध्य ज्ञात करने के लिए आपने किस विधि का प्रयोग किया और क्यों ?
हल
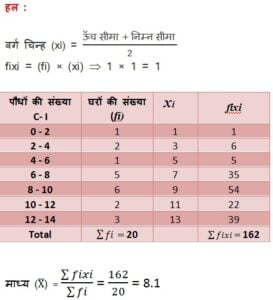
किसी फैक्ट्री के 50 श्रमिकों मज़दूरी के निम्नलिखित बंटन पर विचार कीजिए :
![]()
एक उपयुक्त विधि का प्रयोग करते हुए, इस फैक्ट्री के श्रमिकों की माध्य दैनिक मज़दूरी ज्ञात कीजिए |
हल : प्रत्येक अंतराल के लिए वर्ग-चिन्ह को इस सूत्र से ज्ञात करेंगे

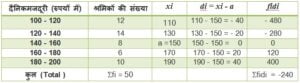
कल्पित माध्य विधि (Assume mean Method) से
Σfidi = – 480 + – 280 + 0 + 120 + 400 = –760 + 520 = –240
Σfi = 50 और a = 150
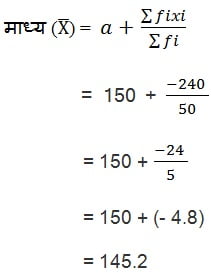
1. निम्नलिखित बंटन एक मोहल्ले के बच्चों के दैनिक जेबखर्च दर्शाता है | माध्य जेबखर्च 18 रू है | लुप्त बारंबारता f ज्ञात कीजिए:

हल :
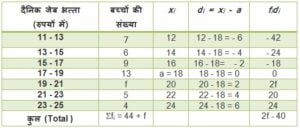
कल्पित माध्य विधि (Assume mean Method) से
Σfidi = 2f – 40, Σfi = 44 + f और a = 18,
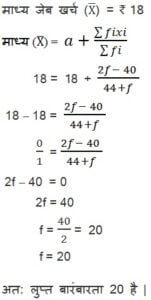
3. किसी अस्पताल में, एक डॉक्टर द्वारा 30 महिलाओं की जाँच की गई और उनके ह्रदय स्पंदन (beat) की प्रति मिनट संख्या नोट करके नीचे दर्शाए अनुसार संक्षिप्त रूप में लिखी गई | एक उपयुक्त विधि चुनते हुए, इन महिलाओं के ह्रदय स्पंदन की प्रति मिनट माध्य संख्या ज्ञात कीजिए :

हल :
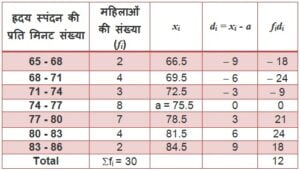
कल्पित माध्य विधि (Assume mean Method) से
Σfidi = 12, Σfi = 30 और a = 75.5,
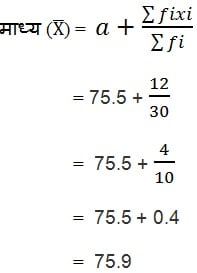
अत: महिलाओं के ह्रदय स्पंदन की प्रति मिनट माध्य संख्या = 75.9 है |
4. किसी फुटकर बाज़ार में, फल विक्रेता पेटियों में रखे आम बेच रहें थे | इन पेटियों में आमों की संख्याएँ भिन्न – भिन्न थी | पेटियों की संख्या के अनुसार, आमों का बंटन निम्नलिखित था :

एक पेटी में रखे आमों की माध्य संख्या ज्ञात कीजिए | आपने माध्य ज्ञात करने की किस विधि का प्रयोग किया है ?
हल: दी गयी श्रृखला समावेशी (inclusive) है जहाँ वर्ग-अंतरालों में 1 का अंतर है | अत: दी गयी श्रृंखला को अपवर्जी (exclusive) श्रृंखला में बदलेंगे |
53 – 52 = 1
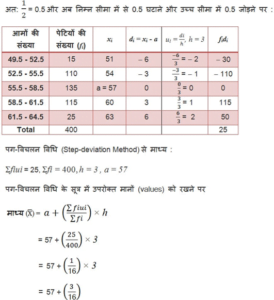
= 57 + 0.1875
= 57.1875 या 57.19
आमों की माध्य संख्या = 57.19
5. निम्नलिखित सारणी किसी मोहल्ले के 25 परिवारों में भोजन पर हुए दैनिक व्यय को दर्शाती है:
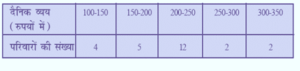
एक उपयुक्त विधि द्वारा भोजन पर हुआ माध्य व्यय ज्ञात कीजिए |
हल :
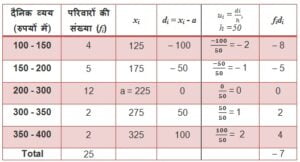
पग-विचलन विधि (Step-deviation Method) से माध्य :
Σfiui = – 7, Σfi = 25, h = 50 , a = 225
पग-विचलन विधि के सूत्र में उपरोक्त मानों (values) को रखने पर

6. वायु में सल्फर डाई – ऑक्साइड (SO ) की सान्द्रता (भाग प्रति मिलियन में ) को ज्ञात करने के लिए, एक नगर के मोहल्लों से आँकड़े एकत्रित किए गये, जिन्हें नीचे प्रस्तुत किया गया है :
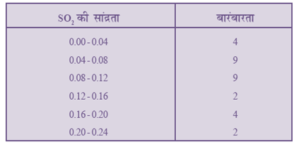
वायु में SO2 की सांद्रता का माध्य ज्ञात कीजिए |
हल :
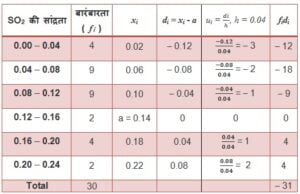
पग-विचलन विधि (Step-deviation Method) से माध्य :
Σfiui = – 31, Σfi = 30, h = 0.04 , a = 0.14
पग-विचलन विधि के सूत्र में उपरोक्त मानों (values) को रखने पर
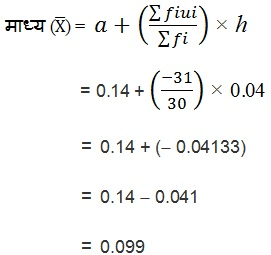
वायु में सल्फर डाई-ऑक्साइड (SO) की सान्द्रता का माध्य = 0.099
किसी कक्षा अध्यापिका ने पुरे सत्र के लिए अपनी कक्षा के 40 विधार्थियों कि अनुपस्थिति निम्नलिखित रूप में रिकॉर्ड (record) की | एक विधार्थी जितने दिन अनुपस्थित रहा उनका माध्य ज्ञात कीजिए :
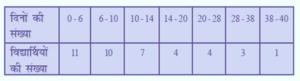
हल :
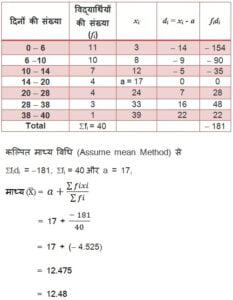
विद्यार्थी की अनुपस्थित का माध्य = 12.48 दिन
निम्नलिखित सारणी 35 नगरों कि साक्षरता दर (प्रतिशत में) दर्शाती है | माध्य साक्षरता दर ज्ञात कीजिए :
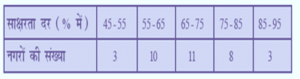
हल :
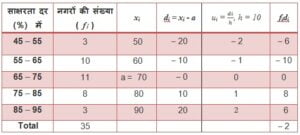
विचलन विधि (Step-deviation Method) से माध्य :
Σfiui = – 2, Σfi = 35, h = 10 , a = 70
पग-विचलन विधि के सूत्र में उपरोक्त मानों (values) को रखने पर
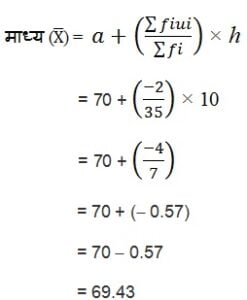
अत: माध्य साक्षरता दर = 69.43 %
निम्नलिखित बारंबारता बंटन किसी मोहल्ले के 68 उपभोक्ताओं की बिजली कि मासिक खपत दर्शाता है | इन आँकड़ों के Ex माध्यक, माध्य और बहुलक ज्ञात कीजिए | इनकी तुलना कीजिए |
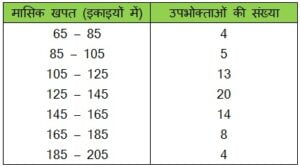
हल :
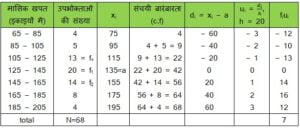
माध्यक (Median) के लिए :
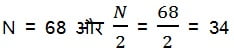
34 संचयी बारंबारता के 42 में शामिल है |
इसलिए, माध्यक वर्ग 125 – 145 है |
अत: l = 125, f = 20, cf = 22 (माध्यक वर्ग से ठीक ऊपर वाला संचयी बारंबारता) और
h = 20,

बहुलक के लिए :
सारणी से हमें ज्ञात होता है कि वर्ग 125 – 145 की बारंबारता सबसे अधिक है इसलिए बहुलक वर्ग 125 – 145 है
अत: l = 125, f0 = 13, f1 = 20, f2 = 14 और h = 20

माध्यक = 137, माध्य = 137.058 और बहुलक = 135.76
यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो तो x और y के मान ज्ञात कीजिए :
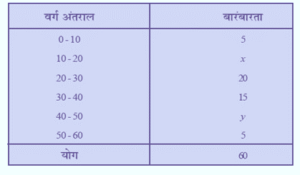
हल :
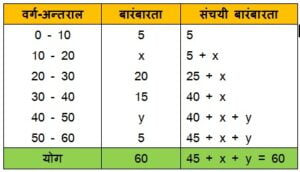
दिया है, माध्यक = 28.5,
अत: 28.5 वर्ग-अन्तराल 20 – 30 में शामिल है |
इसलिए, l = 20, f = 20, h = 10 और cf = 5 + x
N = 60,

अब, 45 + x + y = 60
अथवा x + y = 60 – 45
x + y = 15
8 + y = 15 समी० (1) से
y = 15 – 8
y = 7
x = 8, और y = 7
निम्नलिखित बंटन किसी फैक्ट्री के 50 श्रमिकों कि दैनिक आय दर्शाता है :
![]()
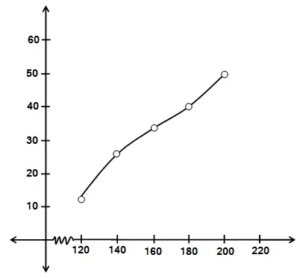
उपरोक्त बंटन को एक कम प्रकार ‘ के संचयी बारंबारता बंटन में बदलिए और उसका तोरण खींचिए |
हल : ‘से कम प्रकार’ का संचयी बारंबारता बंटन सारणी :
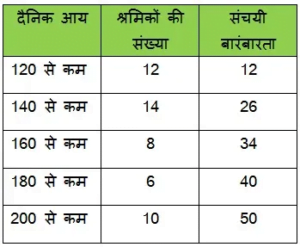
से कम प्रकार’ के तोरण के लिए क्रमित युग्म (order pairs) :
(120, 12), (140, 26), (160, 34), (180, 40) और (200, 50)
We hope that class 10 Math Chapter 14 सांख्यिकी (Statistics) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 14 सांख्यिकी (Statistics) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…