पाठ – 15
प्रायिकता
In this post we have given the detailed notes of class 10 Math chapter 15 Probability in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 15 प्रायिकता के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 15 |
| Chapter Name | प्रायिकता (Probability) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 15 प्रायिकता
प्रायिकता
किसी घटना के घटने या न घटने की सम्भाब्यता को उसकी प्रायिकता कहलाती है। उदाहरण के लिए यदि कोई सिक्का उछाला जाय तो या तो हेड आएगा या टेल आएगा।

इस प्रकार 2 सम्भावना मे 1 हेड या 1 टेल आएगा। दोनों की ही प्रायिकता ![]() होगी।
होगी।
![]()
परिभाषा
किसी भी घटना के घटित होने की संभावना को प्रायिकता के रूप में जाना जाता है। जब कोई घटना घटित होती है, तो अनुकूल परिणामों की संभावनाएँ प्रायिकता का मान होती हैं। उदाहरण के लिए, यदि हम एक सिक्के को उछालते हैं तो चित और पट आने की संभावना बराबर होती है। सिक्का उछालना एक प्रयोग है और चित या पट के आने की संभावना क्रमशः चित या पट के आने की प्रायिकता है। एक चित और एक पट प्राप्त करना इस प्रयोग की घटनाएँ हैं।
प्रायिकता का सूत्र (Formula of the Probability)
किसी भी घटना की प्रायिकता का सूत्र इस प्रकार दिया जाता है:
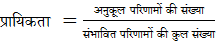
किसी घटना A के लिए, उपरोक्त सूत्र को इस प्रकार लिखा जा सकता है:
घटना A की प्रायिकता, P (A) = घटना A के अनुकूल परिणामों की संख्या / घटना A के परिणामों की कुल संख्या
नोट – उपरोक्त सूत्र केवल सैद्धान्तिक प्रायिकता ज्ञात करने में सहायक है जिसे पारंपरिक प्रायिकता भी कहते हैं।
व्याख्या
प्रायिकता में, प्रत्येक प्रयोग के परिणामों को आदर्श स्थिति में समान माना जाता है। लेकिन व्यावहारिक रूप से हर प्रयोग के परिणाम समान नहीं होते हैं। यदि हम एक सिक्के को समतल सतह पर उछालते हैं तो परिणाम एक चित या एक पट होगा लेकिन यदि हम एक सिक्के को रेत पर उछालते हैं तो परिणाम समान नहीं होंगे क्योंकि सिक्का इसके किनारे के अनुदिश गिर सकता है। इस स्थिति में, तीन परिणाम होंगे लेकिन हम उन पर विचार नहीं करते हैं और आदर्श स्थिति के लिए केवल दो समान परिणामों (चित या पट) पर विचार करते हैं।
इसे स्पष्ट रूप से समझने के लिए हम एक और उदाहरण लेते हैं। एक बॉक्स है और बॉक्स में 5 पेंसिल और 2 पेन हैं और हमें एक पेंसिल या एक पेन निकालने की प्रायिकता ज्ञात करनी है। चूँकि बॉक्स में 5 पेंसिल और 2 पेन हैं इसलिए पेंसिल मिलने की संभावना पेन मिलने से ज्यादा है। इसका मतलब है कि इस प्रयोग के परिणाम समान नहीं हैं।
यह देखते हुए कि सभी प्रयोगों के परिणाम हमेशा समान नहीं होते हैं, इस कक्षा में, हम मान लेंगे कि सभी प्रयोगों के समान परिणाम हैं।
उदाहरण – एक सिक्के को एक बार उछालने पर चित आने की प्रायिकता ज्ञात कीजिए।
हल – इस उदाहरण में, एक सिक्के को एक बार उछाला जाता है, इसलिए दो संभावित परिणाम होंगे चित या पट। मान लीजिए A चित आने की घटना है।
एक सिक्के को एक बार उछालने पर चित आने का परिणाम 1 होता है। इसका अर्थ है कि घटना A के अनुकूल परिणाम 1 है और कुल संभावित परिणाम 2 हैं।
इसलिए,
घटना A की प्रायिकता, P(A) = अनुकूल परिणामों की संख्या / संभावित परिणामों की कुल संख्या
P(A) = ![]()
उत्तर
नोट -1) उपरोक्त उदाहरण में, एक पट प्राप्त करने की संभावना भी ![]() होगी क्योंकि पट प्राप्त करने का अनुकूल परिणाम भी 1 है। माना B पट प्राप्त करने की घटना है। तब
होगी क्योंकि पट प्राप्त करने का अनुकूल परिणाम भी 1 है। माना B पट प्राप्त करने की घटना है। तब
P(A) = ![]() और P(B) =
और P(B) = ![]()
अब दोनों प्रायिकताओं को जोड़ने पर, P(A) + P(B) = ![]() +
+ ![]() = 1
= 1
उपरोक्त व्यंजक से हम यह निष्कर्ष निकाल सकते हैं कि किसी प्रयोग की सभी घटनाओं की प्रायिकताओं का योग 1 होता है।
2) उपरोक्त उदाहरण में, हमने एक चित आने की प्रायिकता ज्ञात की है लेकिन हम यह भी कह सकते हैं कि हमने पट न मिलने की प्रायिकता ज्ञात की है। दोनों प्रायिकताएँ समान हैं। A एक चित आने की घटना है और माना A एक पट न आने की घटना है।
इसलिए, दो समान घटनाएँ P(A) और P(A`) हैं। दोनों घटनाओं को जोड़ने पर,
P(A) + P(A`) = ![]() +
+ ![]() = 1
= 1
जहाँ, P(A) = चित आने की प्रायिकता
P(A`) = पट न आने की प्रायिकता
सामान्य तौर पर, एक घटना E के लिए, हम लिख सकते हैं, P(E) + P(E`) = 1
जहाँ, P(E) = घटना E की प्रायिकता
P(E`) = घटना E की नहीं प्रायिकता
हम यह भी लिख सकते हैं, P(E) = 1 – P(E`) या P(E`) = 1 – P(E)
3) घटना E`, घटना E की पूरक है इसलिए घटना E और घटना E` को पूरक घटना (Complementary Event) कहा जाता है।
प्रायिकता से संबंधित पद (Terms Related to the Probability)
प्रयोग (Experiment) – प्रायिकता ज्ञात करने के लिए कार्य करना एक प्रयोग (Experiment) है। जैसे- एक सिक्का उछालना, पासा फेंकना, डिब्बे में से कोई वस्तु निकालना प्रयोग हैं।



घटना (Event) – किसी प्रयोग के परिणाम को घटना (Event) कहते हैं। उदाहरण के लिए – पासे को फेंकने के बाद कोई संख्या प्राप्त करना एक घटना है।

असंभव घटना (Impossible Event) – यदि किसी घटना की प्रायिकता 0 है तो वह असंभव घटना (Impossible Event) कहलाती है। इस प्रकार की घटना का घटित होना असंभव है।
उदाहरण – एक लकड़ी के बक्से में, 3 नीली गेंदें और 2 लाल गेंदें हैं। एक काली गेंद आने की प्रायिकता ज्ञात कीजिए।

हल – मान लीजिए कि एक काली गेंद प्राप्त होने की घटना A है, लेकिन जैसा कि हम देख सकते हैं कि लकड़ी के बक्से में केवल 3 नीली गेंदें और 2 लाल गेंदें हैं। इसमें कोई काली गेंद नहीं है।
अतः अनुकूल परिणामों की संख्या 0 होगी और संभावित परिणामों की कुल संख्या 3 + 2 = 5 है।
इसलिए,
एक काली गेंद मिलने की प्रायिकता, P(A) = अनुकूल परिणामों की संख्या / कुल संभावित परिणाम
P(A) = 0/5
P(A) = 0
यह एक असंभव घटना का उदाहरण है।
निश्चित घटना (Certain Event)– यदि किसी घटना की प्रायिकता 1 है तो वह घटना निश्चित घटना (Certain Event) कहलाती है। निश्चित घटना को Sure event भी कहा जाता है।
उदाहरण – एक पासे को एक बार फेंकने पर 0 से बड़ी और 7 से छोटी संख्या आने की प्रायिकता ज्ञात कीजिए।
हल – हम जानते हैं कि एक पासे के फलक पर अंकित अंक 1, 2, 3, 4, 5 और 6 हैं। हमें 0 से बड़ी और 7 से छोटी संख्या आने की प्रायिकता ज्ञात करनी है और पासे के फलक पर प्रत्येक अंक 0 से बड़ा और 7 से छोटा है। इसलिए, पासे के फलक पर प्रत्येक संख्या अनुकूल परिणाम है और 6 संख्याएँ हैं इसलिए 6 अनुकूल परिणाम होंगे।
मान लीजिए B, 0 से बड़ी और 7 से छोटी संख्या प्राप्त करने की घटना है और कुल परिणाम भी 6 हैं।
इसलिए, प्रायिकता P(B) = 6/6 = 1
यह एक निश्चित घटना का उदाहरण है।
नोट -1) उपरोक्त उदाहरणों से हम समझ सकते हैं कि प्रायिकता का न्यूनतम मान 0 हो सकता है और प्रायिकता का अधिकतम मान 1 हो सकता है। इसका अर्थ है कि किसी घटना E के लिए प्रायिकता का मान 0 और 1 के बीच होता है या हम लिख सकते हैं 0 ≤ P(E) ≤ 1
2) क्योंकि प्रायिकता का मान 0 और 1 के बीच होता है इसलिए प्रायिकता के सूत्र में अंश (किसी घटना के अनुकूल परिणामों की संख्या) हमेशा हर (संभावित परिणामों की कुल संख्या) से कम या उसके बराबर होता है।
सैद्धांतिक प्रायिकता
किसी घटना E की सैद्धांतिक प्रायिकता जिसे परंपरागत प्रायिकता भी कहा जाता है।ह P(E) निम्नलिखित रूप में परिभाषित की जाती है।
![]()
हल सहित उदाहरण
एक चित प्राप्त करने की प्रायिकता ज्ञात कीजिए, जब एक सिक्के को एक बार उछाला जाता है। साथ ही, एक पट प्राप्त करने की भी प्रायिकता ज्ञात कीजिए।
हल:
एक सिक्के को एक बार उछालने के प्रयोग में, संभव परिणामों की संख्या 2 है: चित (H) और पट (T)। मान लीजिए घटना E ‘चित प्राप्त करना’ है। तब, E के अनुकूल (अर्थात् चित प्राप्त करने के अनुकूल) परिणाम 1 है। अतः,
P(E) = P (चित) = E के अनुकूल परिणामों की सख्ंया/ सभी संभव परिणामों की सख्ंया ![]()
इसी प्रकार, यदि घटना F पट प्राप्त करना है, तो P(F) = P (चित) ![]()
प्रारंभिक घटना
किसी प्रयोग की वह घटना जिसका केवल एक ही परिणाम हो प्रारंभिक घटना कहलाती है। उदाहरण 1 में दोनों घटनाएँ E और F प्रारंभिक घटनाएँ हैं।
ऊपर दिए गए उदाहरण में हम देखते हैं कि P(E) + P(F) ![]()
नोट:
किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग 1 है। यह व्यापक रूप में भी सत्य है।
अभ्यास के लिए प्रश्न
मान लीजिए हम एक पासे को एक बार फेंकते हैं।
(i) 4 से बड़ी संख्या प्राप्त होने की प्रायिकता क्या है?
(ii) 4 से छोटी या उसके बराबर संख्या प्राप्त होने की प्रायिकता क्या है?
हल
(i) यहाँ मान लीजिए कि ‘4 से बड़ी संख्या प्राप्त करना’ घटना E है। सभी संभव परिणाम छः हैं, ये 1, 2, 3, 4, 5 और 6 हैं। स्पष्टतः, घटना E के अनुकूल परिणाम 5 और 6 हैं। अतः E के अनुकूल परिणामों की संख्या 2 है। इसलिए
P(E) = P (4 से बड़ी संख्या) ![]()
(ii) मान लीजिए ‘4 से छोटी या उसके बराबर संख्या प्राप्त करना’ घटना F है। सभी संभव परिणाम = 6 हैं।
घटना F के अनुकूल परिणाम 1, 2, 3 और 4 हैं।
अतः F के अनुकूल परिणामों की संख्या 4 है।
इसलिए ![]()
![]()
क्या उपरोक्त उदाहरण में दी हुई घटना E और F प्रारंभिक घटनाएँ हैं? नहीं, ये प्रारंभिक घटनाएँ नहीं हैं, क्योंकि घटना E के 2 परिणाम हैं तथा घटना F के 4 परिणाम हैं।
स्मरणीय तथ्य
प्रायोगिक प्रायिकता (वास्तविक प्रयोगों के परिणामों पर आधारित थीं।) और सैद्धांतिक प्रायिकता (जिसे पारंपरिक प्रायिकता भी कहते हैं) में अंतर।
घटना E की सैद्धांतिक (या परंपरागत) प्रायिकता P(E) को निम्नलिखित रूप में परिभाषित किया जाता हैः 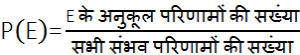
जहाँ हम कल्पना करते हैं कि प्रयोग के सभी परिणाम समप्रायिक हैं।
पूरक घटना
घटना ‘E नहीं’ को निरूपित करने वाली घटना Ē घटना E की पूरक घटना कहलाती है। हम यह भी कहते हैं कि E और Ē परस्पर पूरक घटनाएँ हैं।
व्यापक रूप में, किसी घटना E के लिए यह सत्य है कि P(Ē) = 1 – P(E)
असंभव घटना
उस घटना, जिसका घटित होना असंभव है, की प्रायिकता 0 होती है। ऐसी घटना को एक असंभव घटना कहते हैं।
हल सहित उदाहरण
(i) पासे को एक बार फेंकने पर संख्या 8 प्राप्त करने की क्या प्रायिकता है?
(ii) पासे को एक बार फेंकने पर 7 से छोटी संख्या प्राप्त करने की क्या प्रायिकता है?
हल:
(i) हम जानते हैं कि पासे को एक बार फेंकने पर केवल छः ही संभावित परिणाम हैं। ये परिणाम 1, 2, 3, 4, 5 और 6 हैं। चूँकि पासे के किसी भी फलक पर 8 अंकित नहीं है, इसलिए 8 के अनुकूल कोई भी परिणाम नहीं है, अर्थात् ऐसे परिणामों की संख्या शून्य (0) है। दूसरे शब्दों में, पासे को एक बार फेंकने पर, संख्या 8 प्राप्त करना असंभव है। अतः P(8 प्राप्त करना) ![]()
अर्थात् उस घटना, जिसका घटित होना असंभव है, की प्रायिकता 0 होती है। ऐसी घटना को एक असंभव घटना कहते हैं।
(ii) चूँकि पासे के प्रत्येक फलक पर ऐसी संख्या लिखी है जो 7 से छोटी है, इसलिए पासे को एक बार फेंकने पर यह निश्चित है कि प्राप्त संख्या सदैव 7 से छोटी होगी। अतः, घटना के अनुकूल परिणामों की संख्या सभी संभावित परिणामों की संख्या के बराबर होगी, जो 6 है।
इसलिए, P(E) = P(7 से छोटी संख्या प्राप्त करना) ![]()
निश्चित घटना
अतः उस घटना, जिसका घटित होना निश्चित है, की प्रायिकता 1 होती है। ऐसी घटना को एक निश्चित या निर्धारित घटना कहते हैं।
टिप्पणी:
प्रायिकता P(E) की परिभाषा से, हम देखते हैं कि अंश (घटना E के अनुकूल परिणामों की संख्या) सदैव हर (सभी संभव परिणामों की संख्या) से छोटा होता है या उसके बराबर होता है। अतः,
0 ≤ P(E) ≤ 1
अभ्यास के लिए प्रश्न
अच्छी प्रकार से फेटी गई 52 पत्तों की एक गड्डी में से एक पत्ता निकाला जाता है। इसकी प्रायिकता परिकलित कीजिए कि यह पत्ता:
(i) एक इक्का होगा।
(ii) एक इक्का नहीं होगा।
हल
गड्डी को अच्छी प्रकार से फेटनें से परिणामों का समप्रायिक होना सुनिश्चित हो जाता है।
(i) एक गड्डी में 4 इक्के होते हैं। मान लीजिए घटना E ‘एक इक्का होना’ है।
E के अनुकूल परिणामों की संख्या = 4
सभी संभव परिणामों की संख्या = 52 (क्यों?)
अतः ![]()
(ii) मान लीजिए घटना F ‘एक इक्का नहीं’ है।
माना F के अनुकूल परिणामों की संख्या = 52 – 4 = 48 (क्यों?)
सभी संभव परिणामों की संख्या = 52
अतः ![]()
टिप्पणी:
ध्यान दीजिए कि F और कुछ नहीं बल्कि Ē ही है। अतः, हम P(F) को इस प्रकार भी परिकलित कर सकते हैं:
P(F) = P(Ē) ![]()
स्मरणीय तथ्य
- एक निश्चित (या निर्धारित) घटना की प्रायिकता 1 होती है।
- एक असंभव घटना की प्रायिकता 0 होती है।
- घटना E की प्रायिकता एक ऐसी संख्या P(E) है कि 0 ≤ P(E) ≤ 1
- वह घटना जिसका केवल एक ही परिणाम हो एक प्रारंभिक घटना कहलाती है। किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकता का योग 1 होता है।
- किसी भी घटना E के लिए P(E) + P (Ē) = 1 होता है, जहाँ E घटना ‘ Ē नहीं’ को व्यक्त करता है। E और Ē पूरक घटनाएँ कहलाती हैं।
उदाहरण:
1. एक थैले में 3 लाल और 5 काली गेंदें हैं | इस थैले में से एक गेंद यदृच्छया निकाली जाती है| इसकी प्रायिकता क्या है कि गेंद
(i) लाल हो
(ii) लाल नहीं हो ?
हलः थैले में गेंदों की कुल संख्या = 3 + 5 = 8
थैले में से एक गेंद निकालने की घटना के सभी संभव परिणामों की संख्या = 8

2. एक डिब्बे में 5 लाल कंचे, 8 सफेद कंचे और 4 हरे कंचे हैं | इस डिब्बे में से एक कंचा
(i) लाल है ?
(ii) सफेद है ?
(iii) हरा नहीं है ?
हलः डिब्बे में कंचों की संख्या = 5 लाल कंचे + 8 सफेद कंचे + 4 हरे कंचे = 17 कंचे।
डिब्बे में से एक कंचा निकालने की घटना के सम्भव परिणामों की संख्या = 17
(i) लाल गेंदों की संख्या = 5
डिब्बे में से निकाली गई गेंद का लाल होने की घटना के परिणामों की संख्या = 5
अनुकूल परिणामों की संख्या = 5
अनुकूल परिणामों की संख्या = 5

(ii) सफेद गेंदों की संख्या = 8
डिब्बे में से सफेद गेंद निकाली जाने की घटना के परिणामों की संख्या = 8
अनुकूल परिणामों की संख्या = 8

3. एक पिग्गी बैंक (piggy bank) में, 50 पैसे के सौ सिक्के है, 1 रू के पचास सिक्के हैं, 2 रू के बीस सिक्के गिरने के परिणाम समप्रायिक हैं, तो इसकी क्या प्रायिकता है कि वह गिरा हुआ सिक्का
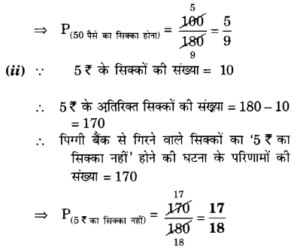
(i) 50 पैसे का होगा ?
(ii) 5 रू का नहीं होगा ?
हलः पिग्गी-बैंक में कुल सिक्कों की संख्या = 50 पैसे के सिक्के + 1 के सिक्के + 2र के सिक्के + 5 के सिक्के
= 100 + 50 + 20 + 10 = 180
पिग्गी बैंक से सिक्का निकलने की घटना के परिणामों की संख्या = 180
(i) 50 पै. के सिक्कों की संख्या = 100
पिग्गी बैंक से 50 पैसे का सिक्का गिरने की घटना की संख्या = 100
4. गोपी अपने जल – जीव कुंड (aquarium) के लिए एक दुकान से मछली खरीदती है | दुकानदार एक टंकी, जिसमें 5 नर मछली और 8 मादा मछली है, में से एक मछली यादृच्छया उसे देने के लिए निकालती है (देखिए आकृति 15.4) | इसकी प्रायिकता है कि निकाली गई मछली नर मछली है?
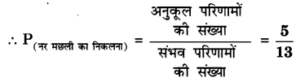
हलः मछलियों की कुल संख्या = (नर मछलियों की संख्या) + (मादा मछलियों की संख्या) = 5 + 8 = 13
कुंड में से मछली निकालने की घटना के परिणामों की कुल संख्या = 13
संभव परिणामों की संख्या = 13
चूंकि नर मछलियों की संख्या = 5
अनुकूल परिणामों की संख्या = 5
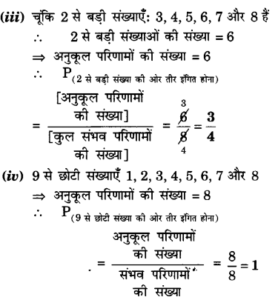
5. संयोग (chance) के एक खेल में, एक तीर को घुमाया जाता है, जो विश्राम में आने के बाद संख्याओं 1,2,3,4,5,6,7, और 8 में से किसी एक संख्या को इंगित करता है (देखिए आकृति 15.5 ) | यदि ये सभी परिणाम समप्रायिक हों तो इसकी क्या प्रायिकता है कि यह तीर इंगित
(i) 8 को करेगा ?
(ii) एक विषम संख्या को करेगा ?
(iii) 2 से बड़ी संख्या को करेगा ?
(iv) 9 से छोटी संख्या को करेगा ?
हलः चूंकि विश्राम में आने पर तीर 1 से 8 तक की किसी भी संख्या को इंगित करता है।
संभव परिणामों की संख्या = 8
(i) चूंकि चक्र पर 8 का एक अंक है।
अंक 8 को इंगित करने की घटना के परिणामों की संख्या = 1
अनुकूल परिणामों की संख्या = 1

6. एक पासे को एक बार फेंका जाता है | निम्नलिखित को प्राप्त करने कि प्रायिकता ज्ञात कीजिए :
(i) एक अभाज्य संख्या
(ii) 2 और 6 के बीच स्थित कोई संख्या
(iii) एक विषम संख्या
हलः
(i) एक पासे पर अभाज्य संख्याएँ 2, 3 और 5 हैं।
माना कि घटना E” एक अभाज्य संख्या प्राप्त करना है।”
E के अनुकूल परिणामों की संख्या = 3
चूंकि पासे पर छः संख्याएँ [1, 2, 3, 45 और 6] होती हैं।
E के संभावित परिणामों की संख्या = 6

एक बच्चे के पास ऐसा पासा है जिसके फलकों पर निम्नलिखित अक्षर अंकित है :

इस पासे को एक बार फेंका जाता है | इसकी क्या प्रायिकता है कि
(i) A प्राप्त हो ?
(ii) D प्राप्त हो ?
हलः चूंकि पासे के 6 फलकों पर अंकित अक्षर इस प्रकार हैं:
![]()
फेंके जाने पर एक अक्षर छः प्रकार से प्राप्त होता है।
सम्भव परिणामों की कुल संख्या = 6
(i) चूंकि दो फलकों पर अक्षर A अंकित है।
अक्षर A दो प्रकार से प्राप्त हो सकता है।
अनुकूल परिणामों की संख्या = 2
माना घटना E “अक्षर A का प्राप्त होना” है,

(ii) चूंकि केवल एक फलक पर अक्षर D अंकित है।
अनुकूल परिणामों की संख्या = 1
माना घटना E “अक्षर D वाला फलक प्राप्त हो” है,

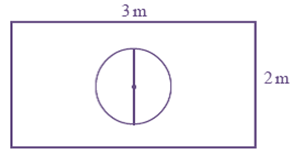
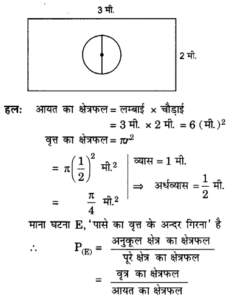
7. मान लीजिये आप एक पासे को आकृति 15.6 में दर्शाए आयताकार क्षेत्र में यादृच्छया रूप से गिराते हैं | इसकी क्या प्रायिकता है कि वह पासा 1m व्यास वाले वृत्त के अन्दर गिरेगा?
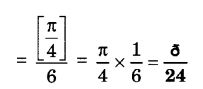
144 बाल पेनों के एक समूह में 20 बाल पेन खराब हैं और शेष अच्छे हैं | आप वाही पेन खरीदना चाहेंगे जो अच्छा हो, परन्तु खराब पेन आप खरीदना नहीं चाहेंगे | दुकानदार इन पेनों में से, यादृच्छया एक पेन निकालकर आपको देता है | इसकी क्या प्रायिकता है कि
(i) आप वह पेन खरीदेंगे ?
(ii) आप वह पेन नहीं खरीदेंगे ?
हलः बॉल पेनों की कुल संख्या = 144
1 पेन निकालने के संभावित परिणामों की संख्या = 144
(i) चूंकि खराब पेनों की संख्या = 20
अच्छे पेनों की संख्या = 144 – 20 = 124
अनुकूल परिणामों की संख्या = 124
माना घटना E, “अच्छा पेन खरीदना” है।

उदाहरण 13 को देखिए | (i) निम्नलिखित सारणी को पूरा कीजिए :

(ii) एक विधार्थी यह तर्क देता है कि ‘यहाँ कुल 11 परिणाम 2,3,4,5,6,7,8,9,10,11 और 12 है | अतः प्रत्येक कि प्रायिकता 1/11 है|’ क्या आप इस तर्क से सहमत है ? सकारण उत्तर दीजिए |
हलः जब नीला पासा ‘1’ दर्शाता है, तो सलेटी पासे पर संख्याओं 1, 2, 3, 4, 5, 6 में से कोई भी संख्या हो सकती है। यही तब भी होगा, जब नीले पासे पर ‘2’, ‘3’, ‘4’, ‘5’ या ‘6’ होगा। इस प्रयोग के संभावित परिणामों को नीचे सारणी में दिया गया है। प्रत्येक क्रमित युग्म की पहली संख्या नीले पासे पर आने वाली संख्या है तथा दूसरी संख्या सलेटी पासे पर आने वाली संख्या है।
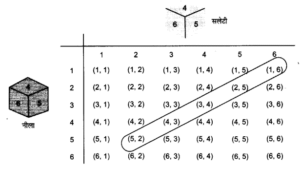
ध्यान रहे कि युग्म (1, 4) और (4, 1) भिन्न है। इस प्रकार सभी संभव परिणाम = ![]()
(1) दोनों पासों की संख्याओं का योग 8
घटना “दोनों पासों की संख्याओं का योग 8 है’’ को E से प्रकट करें तो,
E के अनुकूल परिणाम हैं; (2, 6), (3, 5), (4, 4), (5, 3) और (6, 2) हैं। जैसा कि उक्त आकृति में दर्शाया गया है।
इन युग्मों की संख्या 5 है।
![]()
(2) दोनों पासों की संख्याओं का योग 13
उक्त आकृति से स्पष्ट है कि ऐसा कोई भी परिणाम नहीं है जब दोनों पासों की संख्याओं का योग 13 हो।
यदि घटना “दोनों पासों की संख्याओं का 13 है” को F द्वारा व्यक्त किया जाता हो, तो
F के अनुकूल परिणामों की संख्या = 0
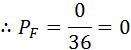
(3) दोनों पासों की संख्याओं का योग < 12
उक्त आकृति से स्पष्ट है कि दोनों पासों की संख्याओं के युग्मों की संख्याओं का योग 12 से कम है या 12 समान है। यदि उक्त घटना, “दोनों पासों की संख्याओं का योग < 12 है” को G व्यक्त करें, तो G के अनुकुल परिणामों की संख्या = 36
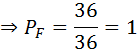
(4) (a) दो पासों के अंकों का योग 3 होना
चूंकि (1, 2) और (2, 1) ऐसे युग्म हैं जिनकी संख्याओं का योग 3 है। इन युग्मों (परिणामों) की संख्या 2 है।
यदि उक्त घटना को पत्र से प्रकट करें, तो H के अनुकूल परिणामों की संख्या = 2
![]()
(b) दोनों पासों की संख्याओं का योग 4 है
चूंकि (1, 3), (2, 2), (3, 1) ऐसे युग्म हैं जिनकी संख्याओं का योग 4 है। इनकी संख्या 3 है।
यदि उक्त घटना को J, से व्यक्त करें, तो J के अनुकूल परिणामों की संख्या = 3
![]()
(c) दोनों पासों की संख्याओं का योग 5 है
स्पष्ट है कि ऐसे युग्मों की संख्या 4 है जिनमें संख्याओं का योग 5 है [.-.. (1, 4), (2, 3), (3, 2) और (4, 1)) की
संख्याओं का योग 5 है।
यदि उक्त घटना को k से व्यक्त करें, तो k के अनुकूल परिणामों की संख्या = 4
![]()
(d) दोनों पासों की संख्याओं का योग 6 है
मात्रा उक्त घटता को (L) से व्यक्त करते हैं।
![]() , के परिणाम हैं: (1, 5), (2, 4), (3, 3), (4, 2) और (5, 1)
, के परिणाम हैं: (1, 5), (2, 4), (3, 3), (4, 2) और (5, 1)
![]() , के अनुकूल परिणामों की संख्या = 5
, के अनुकूल परिणामों की संख्या = 5
![]()
(e) दोनों पासों की संख्याओं का योग 7 है
उक्त आकृति से स्पष्ट है कि (1, 6) (2, 5), (3, 4), (4, 3), (5, 2) और (6, 1) ऐसे 6 युग्म हैं जिनमें संख्याओं का योग 7 है;
यदि इस घटना को M से प्रकट करें, तो M के अनुकूल परिणामों की संख्या = 6
![]()
(f) दोनों पासों की संख्याओं का योग 9 है
स्पष्ट है कि: (3, 6), (4, 5), (5, 4) और (6, 3) ऐसे 4 युग्म हैं जिनमें संख्याओं का योग 9 है।
* यदि इस घटना को (N) से व्यक्त करें, तो N अनुकूल परिणामों की संख्या = 4
![]()
(g) दोनों पासों की संख्याओं का योग 10 है
चूंकि (4, 6), (5, 5), (6, 4) ऐसे 3 युग्म हैं जिनमें संख्याओं का योग 10 है।
इस घटना को यदि (p) से व्यक्त करें, तो p के अनुकूल परिणामों की संख्या = 3

(h) दोनों पासों की संख्याओं का योग 11 है
स्पष्ट है कि: (5, 6) और (6, 5) केवल दो ही ऐसे युग्म हैं जिनमें संख्याओं का योग 11 है। यदि इस घटना को (Q) से व्यक्त करें, तो Q के अनुकूल परिणामों की संख्या = 2
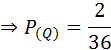
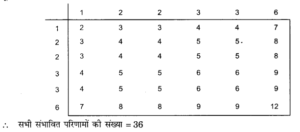
इस प्रकार दी गई तालिका को हम निम्नाकिंत रूप से पूरा करते हैं:
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
(v) नहीं। चूंकि सभी संभव परिणामों की संख्या 36 है, 11 नहीं
![]() यह तर्क सही नहीं है।
यह तर्क सही नहीं है।
एक पासे को दो बार फेंका जाता है | इसकी क्या प्रायिकता है कि
(i) 5 किसी भी बार में नहीं आएगा ?
(ii) 5 कम से कम एक बार आएगा ?
[संकेत : एक पासे को दो बार फेंकना और दो पासों को एक साथ फेंकना एक ही प्रयोग माना जाता है |]
हलः एक पासे को दो बार फेंकना या दो पासों को एक साथ फेंकना एक ही घटना है।
सभी संभव परिणाम इस प्रकार हैं:


एक पासे के फलकों पर संख्याएँ 1,2,2,3,3, और 6 लिखी हुई हैं | इसे दो बार फेंका जाता है तथा दोनों बार प्राप्त हुई संख्याओं के योग लिख लिए जाते हैं | दोनों बार फेंकने के बाद, प्राप्त योग के कुछ संभावित मान निम्नलिखित सारणी में दिए हैं इस सारणी को पूरा कीजिए |
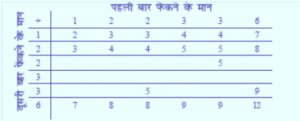
इसकी क्या प्रायिकता है कि कुल योग
(i) एक सम संख्या होगा ?
(ii) 6 है ?
(iii) कम से कम 6 है ?

एक जार में 24 कंचे है जिनमे कुछ हरे हैं और शेष नीले हैं। यदि इस जार में से यादृच्छया एक कंचा निकाला जाता है तो इस कंचे के हरा होने कि प्रायिकता 2/3 है। जार में नीले कंचों कि संख्या ज्ञात कीजिए।
हलः चूंकि जार में 24 कंचे हैं।
सभी संभव परिणामों की संख्या = 4
माना जार में नीले कचे x हैं।
जार में हरे कंचों की संख्या = 24 – x
यदि घटना “निकाला गया कंचा हरा है” को E से व्यक्त करें, तो
E के अनुकूल परिणामों की संख्या = (24 – x)

We hope that class 10 Math Chapter 15 प्रायिकता (Probability) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 15 प्रायिकता (Probability) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…