पाठ – 6
त्रिभुज
In this post we have given the detailed notes of class 10 Math chapter 6 Triangles in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 6 त्रिभुज के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 6 |
| Chapter Name | त्रिभुज (Triangles) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 6 त्रिभुज
त्रिभुज क्या है
तीन रेखाखण्डों से घिरी हुई समतलीय आकृति त्रिभुज कहलाती है। त्रिभुज को ∆ से निरूपित किया जाता है। एक त्रिभुज की तीन भुजाएँ, तीन कोण और तीन शीर्ष होते हैं। त्रिभुज के तीनों कोणों का योग 180° होता है।
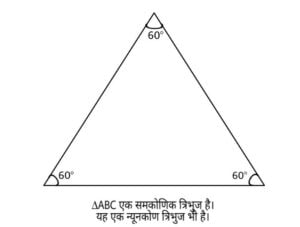
त्रिभुजों का वर्गीकरण
त्रिभुजों का वर्गीकरण निम्नलिखित दो आधार पर किया जा सकता है:
- (i) भुजाओं के आधार पर
- (ii) कोणों के आधार पर
भुजाओं के आधार पर त्रिभुज
भुजाओं के आधार पर त्रिभुज तीन प्रकार के होते हैं:
- विषमबाहु त्रिभुज
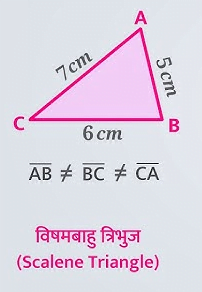
- समद्विबाहु त्रिभुज
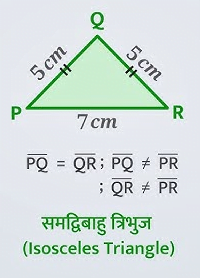
- समबाहु त्रिभुज
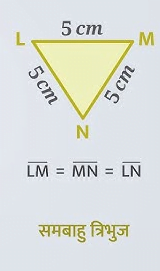
कोणों के आधार पर त्रिभुज
कोणों के आधार पर त्रिभुज तीन प्रकार के होते हैं:
- न्यून कोण त्रिभुज
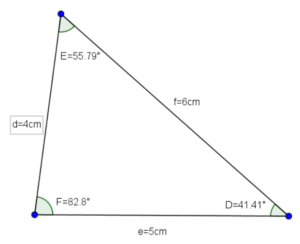
- अधिक कोण त्रिभुज
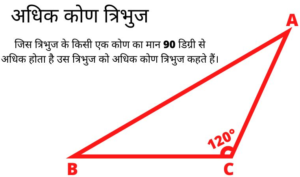
- समकोण त्रिभुज
सभी सर्वांगसम आकृतियाँ समरूप होती हैं, परंतु सभी समरूप आकृतियों का सर्वांगसम होना आवश्यक नहीं है।
सर्वांगसम त्रिभुज
जब दो त्रिभुज की सारी भुजाओं एवं कोणों का माप समान होता है तो वे त्रिभुज सर्वांगसम होते हैं।
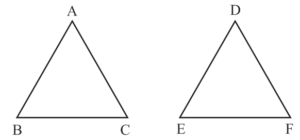
समरूप त्रिभुज
दो त्रिभुज समरूप होंगे यदि
(i) यदि दो त्रिभुजों में, संगत कोण समान हों, तो त्रिभुज समरूप होते हैं।
(ii) यदि दो त्रिभुजों की संगत भुजाएँ समानुपाती हों, तो त्रिभुज समरूप होते हैं।
(iii) यदि एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो तथा उन कोणों को बनाने वाली भुजाएँ समानुपाती हों, तो त्रिभुज समरूप होते हैं।
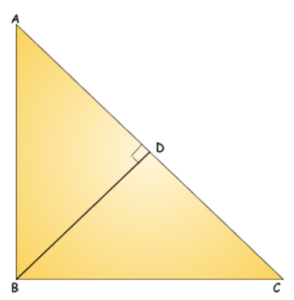
सर्वांगसमता के प्रकार
(i) AAS (कोण-कोण-भुजा):
यदि दो त्रिभुजों के कोणों के दो युग्म माप में बराबर हों, और संगत गैर-शामिल भुजाओं का एक युग्म लंबाई में बराबर हो, तो त्रिभुज सर्वांगसम होते हैं। …
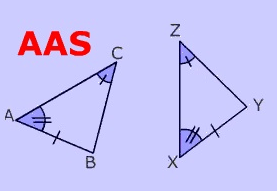
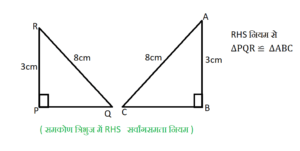
(ii) RHS (समकोण-कर्ण-पक्ष):
यदि दो समकोण त्रिभुजों के कर्णों की लंबाई समान है, और छोटी भुजाओं का एक युग्म लंबाई में समान है, तो त्रिभुज सर्वांगसम होते हैं।
कोणों के आधार पर त्रिभुज के प्रकार
कोणों के आधार पर त्रिभुज तीन प्रकार के होते हैं:
- न्यून कोण त्रिभुज: (उस त्रिभुज को कहते हैं जिसके तीनों कोण, न्यूनकोण (90° से कम) हों।)
- अधिक कोण त्रिभुज: (उस त्रिभुज को कहते हैं जिसका कोई एक कोण, अधिककोण (90° से अधिक) हो।)
- समकोण त्रिभुज: (जिसका एक कोण 90 अंश का (अर्थात, समकोण) हो।)
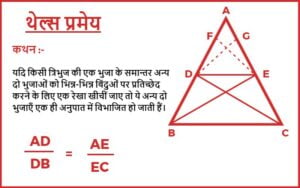
थेल्स (Thales) के प्रमेय
ज्यामिति में थेल्स के प्रमेय (Thales’ theorem) के अनुसार किसी भी वृत्त के परिधि पर स्थित तीन बिन्दुओं A, B तथा C हो तो कोण ABC का मान ९० अंश होगा यदि AC उस वृत्त का कोई व्यास हो। यह प्रमेय ‘अन्तःनिर्मित कोण प्रमेय’ (inscribed angle theorem) का एक विशेष रूप है।
प्रश्न: बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं:
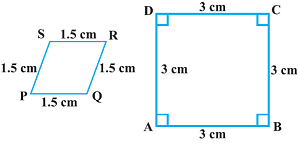
हल: दिये गये चतुर्भुज समरूप नहीं है।
चूँकि दोनों आकृतियों के संगत भुजा समानुपाती हैं परंतु संगत कोण बराबर नहीं हैं।
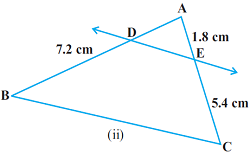
प्रश्न: आकृति (i) और (ii) में, DE||BC है। (i) में EC और (ii) में AD ज्ञात कीजिए:
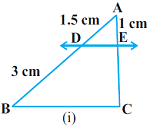
हल: दिया गया है:
चित्र (i) में
AD = 1.5 cm
BD = 3 cm
AE = 1 cm
तथा DE || BC
तब EC = ?
अत: थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार
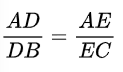
चित्र से AD, DB तथा AE का मान रखने पर,
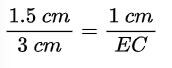
बज्र गुणन (Cross multiplication) करने पर हम पाते हैं कि
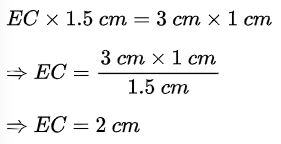
चित्र (ii) में:

DB = 7.2 cm
AE = 1.8 cm
EC = 5.4 cm तथा
DE || BC
तब, AD=?
थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार
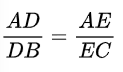
DB, AE तथा EC का मान रखने पर, हम पाते हैं कि
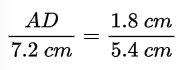
बज्र गुणन (Cross multiplication) करने पर हम पाते हैं कि
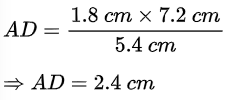
अत: (i) में EC = 2 cm और (ii) में AD = 2.4 cm उत्तर
प्रश्न: किसी ![]() PQR की भुजाओं PQ और PR पर क्रमश: बिन्दु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है:
PQR की भुजाओं PQ और PR पर क्रमश: बिन्दु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है:
- (i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
- (ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
- (iii) PQ =1.28 cm, PR = 2.56 cm, PE = 0.18 cm, और PF = 0.36 cm
हल: मान लिया कि दिया गया त्रिभुज चित्र के अनुसार है,
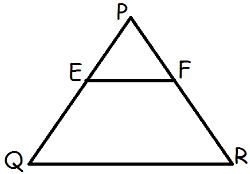
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार हम जानते हैं कि
यदि EF || QR, तो

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm और RF = 9 cm
थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार हम जानते हैं कि
यदि EF || QR, तो
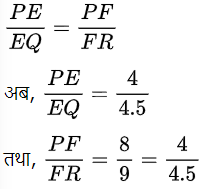
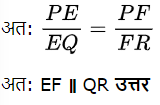
(iii) PQ =1.28 cm, PR = 2.56 cm, PE = 0.18 cm, और PF = 0.36 cm
थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार हम जानते हैं कि
यदि EF || QR, तो

प्रश्न: आकृति में यदि LM ∥ CB और LN ∥ CD हो तो सिद्ध कीजिए कि
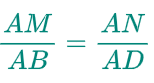
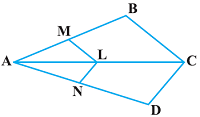
हल: दिया गया है, LM ∥ CB
अत: ![]() ABC ~
ABC ~ ![]() AML
AML
अत: थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार हम जानते हैं कि
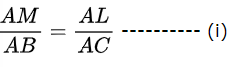
पुन: दिया गया है, LN ∥ CD
अत: ![]() ACD ~
ACD ~ ![]() ALN
ALN
अत: थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार हम जानते हैं कि
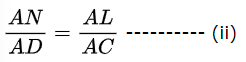
अत: समीकरण (i) तथा (ii) से
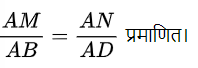
प्रश्न 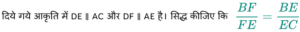
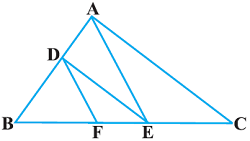
हल: दिया गया है, DE ∥ AC
अत: ![]() ABC ~
ABC ~ ![]() DBE
DBE
अत: थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार
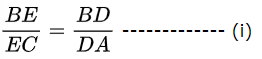
पुन: दिया गया है, DF ∥ AE
अत: ![]()
अत: थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार
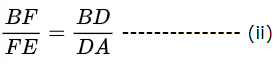
अत: समीकरण (i) तथा (ii) से
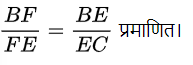
प्रश्न: आकृति में DE ∥ OQ और DF∥OR है। दर्शाइए कि EF ∥ QR है।
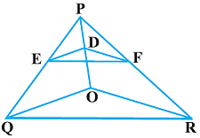
हल: दिया गया है, DE ∥ OQ
![]()
थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार
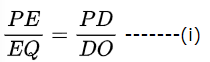
पुन: दिया गया है, DF ∥ OR
![]()
थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार
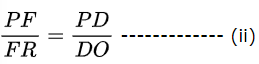
अब समीकरण (i) तथा (ii) के द्वारा,
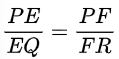
अत: आधारभूत समानुपातिकता प्रमेय के विलोम के अनुसार
EF ∥ QR प्रमाणित।
प्रश्न: दिये गये आकृति में क्रमश: OP, OQ और OR पर स्थित बिन्दु A, B और C इस प्रकार हैं कि AB ∥ PQ और AC ∥ PR है। दर्शाइए कि BC ∥ QR है।
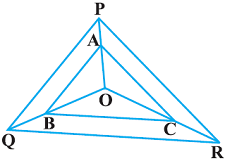
हल: दिया गया है, AB ∥ PQ
![]()
थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार
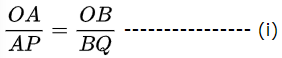
पुन: दिया गया है, AC ∥ PR
![]()
थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय के अनुसार
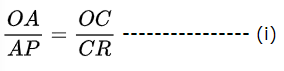
अब समीकरण (i) तथा (ii) से
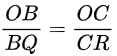
अत: थेल्स (Thales) के प्रमेय अर्थात आधारभूत समानुपातिकता प्रमेय विलोम के अनुसार
BC ∥ QR प्रमाणित
प्रश्न: प्रमेय का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य बिन्दु से होकर दूसरी भुजा के समांतर खींची गए रेखा तीसरी भुजा को समद्विभाजित करती है। (याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं)
हल:

मान लिया कि PQR एक त्रिभुज है, तथा बिन्दु E इस त्रिभुज के PQ भुजा पर मध्य बिन्दु है।
अत: PE = EQ (चूँकि E इस भुजा का मध्य बिन्दु है)
अब EF रेखा त्रिभुज की भुजा QR के समानांतर खींची गई।
अब चूँकि EF ∥ QR
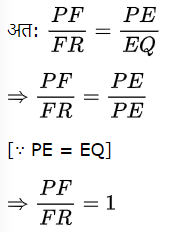
बज्र गुणन करने पर हम पाते हैं कि
![]()
अत: EF रेखा त्रिभुज की तीसरी भुजा AR को समद्विभाजित करती है। प्रमाणित
प्रश्न: बताइए कि दिये गये आकृति में दिये गये त्रिभुजों के युग्मों में से कौन कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
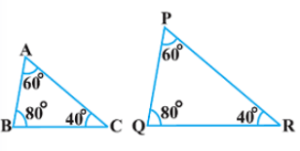
हल: दिये गये त्रिभुजों में,
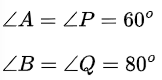
तथा
![]()
![]()
(ii)
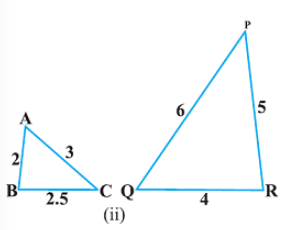
हल: दिये गये त्रिभुजों में,
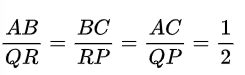
![]()
(iii)
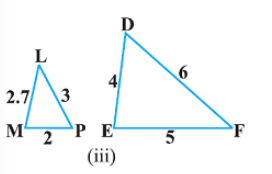
हल: चूँकि दिये गये दोनों त्रिभुजों की भुजाएं न तो बराबर हैं और न ही अनुपात में हैं।
![]()
(iv)
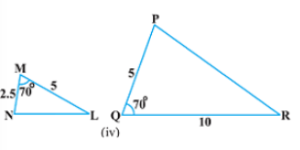
हल: दिये गये त्रिभुजों में
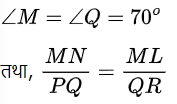
अत: SAS के प्रमेय के अनुसार,
![]()
(v)
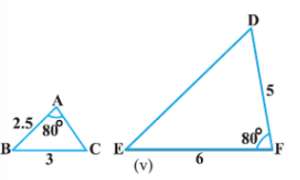
हल: चूँकि संबंधित भुजाएं समान अनुपात में नहीं हैं,
![]()
(vi)
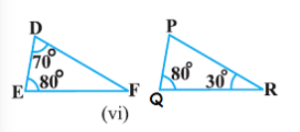
हल:
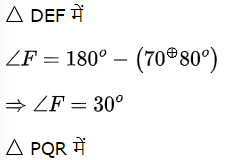
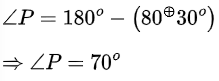
चूँकि दिये गये त्रिभुजों के कोण बराबर हैं,
अत: AAA के अनुसार
![]()
प्रश्न 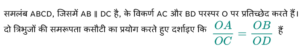
हल:
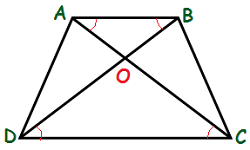
मान लिया कि दिया गया समलंब ABCD है।
जिसमें AB ∥ DC है, तथा विकर्ण AC तथा BD एक दूसरे को O पर प्रतिच्छेद करते हैं।
![]()
![]()
फिर,
![]()
[चूँकि AB || CD अत: ये एकांतर अंत: कोणों के युग्म (Pairs of alternate interior angles) हैं]
तथा,
![]()
[उर्ध्वाकार सम्मुख कोण हैं।]
अत: AAA (कोण-कोण-कोण) कसौटी के द्वारा
![]()
चूँकि समरूप त्रिभुज के संगत भुजा समानुपाती होते हैं।
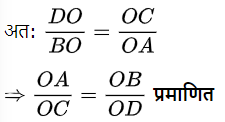
प्रश्न: मान लिजिए कि ![]() AB ~
AB ~ ![]() DEF है और इनके क्षेत्रफल क्रमश : 64 cm2 और 121 cm2 हैं। यदि EF = 15.4 cm हो, तो BC ज्ञात कीजिए।
DEF है और इनके क्षेत्रफल क्रमश : 64 cm2 और 121 cm2 हैं। यदि EF = 15.4 cm हो, तो BC ज्ञात कीजिए।
हल:
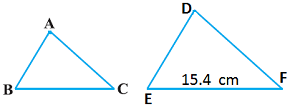
मान लिया कि ABC तथा DEF दो त्रिभुज हैं।
दिया गया है,
![]()
ar (ABC) = 64 cm2
ar (DEF) = 121 cm2
तथा, EF = 15.4 cm
अत: BC = ?
हम जानते हैं कि यदि दो त्रिभुज ABC तथा DEF समरूप हों, तो

अत: BC = 11.2 cm उत्तर
प्रश्न: यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
हल: मान लिया कि ABC तथा PQR दो सर्वांगसम त्रिभुज हैं।
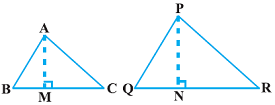
हम जानते हैं कि, यदि
![]()
![]()
दिया गया है, ar (ABC) = ar(PQR)
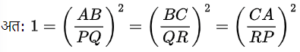
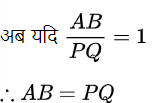
उसी तरह, BC = QR तथा CA = RP
अत: SSS (भुजा-भुजा-भुजा) कसौटी के आधार पर
![]()
अर्थात दोनों त्रिभुज सर्वांगसम हैं प्रमाणित
We hope that class 10 Math Chapter 6 त्रिभुज (Triangles) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 6 त्रिभुज (Triangles) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…