पाठ – 7
निर्देशांक ज्यामिति
In this post we have given the detailed notes of class 10 Math chapter 7 Coordinate Geometry in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 7 निर्देशांक ज्यामिति के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 7 |
| Chapter Name | निर्देशांक ज्यामिति (Coordinate Geometry) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 7 निर्देशांक ज्यामिति
निर्देशांक ज्यामिति
निर्देशांक ज्यामिति गणित की वह महत्वपूर्ण शाखा है जिसमें समतल आकृति पर बने बिन्दुओं की स्थिति को दो संख्याओं के जोड़े के रूप में परिभाषित किया जाता है. संख्याओं के जोड़ों से बने बिंदु की स्थिति को बिंदु निर्देशांक कहते हैं।
निर्देशांक ज्यामिति की परिभाषा
निर्देशांक ज्यामिति गणित की वह महत्वपूर्ण शाखा है जिसमें समतल आकृति पर बने बिन्दुओं की स्थिति को दो संख्याओं के जोड़े के रूप में परिभाषित किया जाता है. संख्याओं के जोड़ों से बने बिंदु की स्थिति को बिंदु निर्देशांक कहते हैं.
दुसरें शब्दों में, ज्यामितिय शाखाओं का वह समूह है, जहां निर्देशांक का उपयोग करके एक बिंदु की स्थिति को परिभाषित किया जाता है, वह निर्देशांक ज्यामिति कहलाता है.
Nirdeshank Jyamiti का प्रयोग किसी दो बिन्दुओं के बिच की दुरी, केंद्र से दुरी बिन्दुओं का विभाजन आदि करने के लिए किया जाता है.
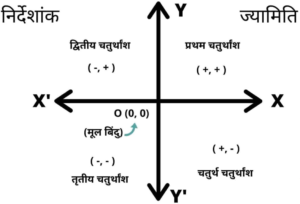
निर्देशांक ज्यामिति के चतुर्थांश
- XOX’ क्षैतिज अक्ष है. इसे x अक्ष भी कहते है.
- YOY’ उर्ध्वादर अक्ष है. इसे y अक्ष भी कहते है.
- XOX’ तथा YOY’ रेखाएं एक दुसरें को O बिंदु पर लम्बवत कटती है.
- XOY तल को प्रथम चरण अथवा कोटि (Quadrant) कहते है.
- X’OY तक को द्वितीय चरण कहते है.
- X’OY’ तल को तृतीय चरण कहते है.
- XOY’ तल को चतुर्थ चरण कहते है.
चतुर्थांश का चिन्ह
- प्रथम पाद यानि चरण = ( +, + )
- द्वितीय पाद = ( -, + )
- तृतीय पाद = ( -, – )
- चतुर्थ पाद = ( +, – )
निर्देशांक ज्यामिति {Coordinate Geometry}
- XX’ अक्ष का धन भाग = ( +, 0 )
- XX’ का ऋण भाग = ( -, 0 )
- YY’ अक्ष का धन भाग = ( 0, + )
- YY’ अक्ष का ऋण भाग = ( 0, – )
- मूल बिंदु = ( 0, 0 )
Note:
XX’ अक्ष के प्रत्येक बिंदु Y नियामक शून्य होता है।
YY’ अक्ष के प्रत्येक बिंदु पर x नियामक शून्य होता है।
मूल बिंदु पर x नियामक तथा y नियामक दोनों शून्य होते है।
- भुज (abscissa) – किसी बिंदु की y-अक्ष से दुरी को x-निर्देशांक अथवा भुज कहते हैं।
- कोटि (ordinate) – किसी बिंदु की x-अक्ष से दुरी को y-निर्देशांक अथवा कोटि कहते हैं।
- किसी बिंदु के भुज और कोटि (x, y) के रूप में होते हैं।
- दो बिंदुओं A(x1, y1) और B(x2, y2) के बीच की दुरी इस सूत्र के हल के बराबर होती है –
- किसी बिंदु A(x, y) की मूलबिन्दु से दूरी इस सूत्र के हल के बराबर होती है –
- बिंदुओं A(x1, y1) और B(x2, y2) को जोड़ने वाले रेखाखंड (line segment) को m1:m2 के अनुपात में आंतरिक रूप से विभाजित करने वाले उस बिंदु L(x, y) के निर्देशांक (coordinates) ये होते हैं –
इसे विभाजन सूत्र (split formula) कहते हैं।
- यदि कोई P रेखाखंड AB को k:1 में विभाजित करता है, तो बिंदु P के निर्देशांक निम्नलिखित होते हैं –
- दो बिंदुओं A(x1, y1) और B(x2, y2) को मिलाने वाले रेखाखंड के मध्यबिंदु (mid-point) के निर्देशांक ये होते हैं –
- कार्तीय तल (cartesian plane) पर स्थित तीन बिंदुओं A(x1, y1), B(x2, y2) और C(x3, y3) से बने
दुरी सूत्र (Distance Formula)
एक बिंदु x- अक्ष और दूसरा बिंदु y- अक्ष पर स्थित किसी भी दो निर्देशांक बिंदु के बीच की दूरी ज्ञात के लिए निम्न फार्मूला का प्रयोग किया जाता है. दुरी सूत्र का प्रयोग क्लास 10th और 12th में अधिक प्रयोग होता है.
दूरी सूत्र (Distance formula) = √[(x2-x1)² + (y2-y1)²]
![]()
Note:
- x1 – रेखा के पहले बिंदु का x- निर्देशांक
- x2 – रेखा के दूसरे बिंदु का x- निर्देशांक
- y1 – रेखा के पहले बिंदु का y- निर्देशांक
- y2 – रेखा के दूसरे बिंदु का y- निर्देशांक
x- अक्ष पर स्थिर बिन्दुओं का निर्देशांक (x, 0) यानी y- निर्देशांक शून्य तथा y- अक्ष पर स्थिर बिन्दुओं का निर्देशांक (0, y) यानी x- निर्देशांक शून्य होता हैं और मूल बिंदु का निर्देशांक (0, 0) होता हैं.
मध्य बिंदु का सूत्र
किसी भी दो निर्देशांक बिंदु के बीच के मध्य निर्देशांक बिंदु ज्ञात करने के लिए मध्य बिंदु सूत्र की प्रयोग किया जाता है.
जहाँ, A कोई बिंदु है जिसका निर्देशांक A (x1, y1) है तथा दूसरा बिंदु B, जिसका निर्देशांक B (x2, y2) है. इस स्थति में मध्य बिंदु के निर्देशांक P (x, y) होगा.
x = (x1 + x2)/2
और
y = (y1 + y2) /2
P निर्देशांक = [ ( x1 + x2 )/2 , ( y1 + y2 )/2]

जहाँ
- x1 – रेखा के पहले बिंदु का x- निर्देशांक
- x2 – रेखा के दूसरे बिंदु का x- निर्देशांक
- y1 – रेखा के पहले बिंदु का y- निर्देशांक
- y2 – रेखा के दूसरे बिंदु का y- निर्देशांक
विभाजन सूत्र
कोई बिंदु, किसी रेखा को किसी भी अनुपात में विभाजन करता है, तो उस बिंदु के निर्देशांक ज्ञात करने के लिए निम्न फार्मूला का प्रयोग किया जाता है.
मान कि कोई रेखा A और B है, जिसमे A बिंदु के निर्देशांक A (x1, y1) और B बिंदु के निर्देशांक B (x2, y2) है, को m:n के रूप में विभाजित किया जाता है. तो इसे ज्ञात करने के लिए इस फार्मूला का प्रयोग होता है.
x = (m × x2 + n × x1) /m+n
और
y = (m × y2 + n × y1) /m+n, अर्थात
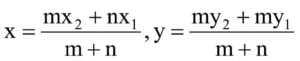
जहाँ
- x1 – रेखा के पहले बिंदु का x- निर्देशांक
- x2 – रेखा के दूसरे बिंदु का x- निर्देशांक
- y1 – रेखा के पहले बिंदु का y- निर्देशांक
- y2 – रेखा के दूसरे बिंदु का y- निर्देशांक
- m – रेखा के विभाजन के अनुपात का पहला भाग
- n – रेखा के विभाजन के अनुपात का दूसरा भाग
रेखा के विभाजन से प्राप्त बिंदु m:n के रूप का होगा.
त्रिभुज का क्षेत्रफल | Area of Triangle
आमतौर पर त्रिभुज का क्षेत्रफल ज्ञात करने के लिए कई अन्य फार्मूला है लेकिन Nirdeshank Jyamiti में क्षेत्रफल निकालने के लिए विशेष फार्मूला का प्रयोग किया जाता है. जो इसके बिन्दुओं पर आधारित होता है.
सामान्य फार्मूला:
- त्रिभुज का क्षेत्रफल = 1/2 × आधार × शीर्षलंब
लेकिन यदि निर्देशांक से बने त्रिभुज का क्षेत्रफल ज्ञात करना हो, तो इस फार्मूला का प्रयोग होता है.
माना कि किसी त्रिभुज के तीन बिन्दुएँ A, B, और C है, जिसका निर्देशांक A (x1, y1) , B (x2, y2) और C (x3, y3) है, तो त्रिभुज का क्षेत्रफल
∆ABC का क्षेत्रफल = 1/2[x1(y2–y3) + x2(y3–y1) + x3(y1–y2)], अर्थात
![]()
जहाँ, A (x1, y1), B (x2, y2) और C (x3, y3) त्रिभुज के निर्देशांक है.
त्रिभुज का क्षेत्रफल के लिए सूत्र –
- आपको कार्तीय तल पर स्थित कुछ बिंदु दिए गए हैं तो पहले उन्हें अंकित करो और फिर आगे हल करो।
- दिए गए बिंदुओं के बीच यदि कोई सम्बन्ध (relation) पाया जाता है, तो उस सम्बन्ध के आधार पर बिना कार्तीय तल के भी उत्तर प्राप्त करना सम्भव (possible) है।
- यदि कोई बिंदु P(x, y) दो अन्य बिंदुओं Q(x1, y1) और R(x2, y2) से समदूरस्थ (समान दुरी पर/ equidistant) हो,
निर्देशांक ज्यामिति से सम्बंधित महत्वपूर्ण तथ्य
किसी तल पर किसी बिंदु की स्थिति निर्धारित करने के लिए , निर्देशांक के अक्षो के युग्म की आवश्यकता होती है. किसी बिंदु का y- अक्ष यानि y-axis से दूरी , उस बिंदु का x- निर्देशांक या भुज कहलाती है. किसी बिंदु की x- अक्ष से दूरी, उस बिंदु का y-निर्देशांक या कोटि कहलाती है.
इसी प्रकार, x- अक्ष पर स्थित किसी बिंदु के निर्देशांक (x, 0) तथा y- अक्ष पर स्थित किसी बिंदु के निर्देशांक (0, y) के रूप का होता है. उम्मीद करता हूँ की Nirdeshank Jyamiti से सम्बंधित अब कोई संदेह शेष नही होगा.
बिंदु निर्देशांक की स्थिति
किसी बिंदु की स्थिति निर्धारित करने के लिए, हमें निर्देशांक अक्षों के एक युग्म की आवश्यकता होती है। किसी बिदु की y-अक्ष से दूरी उस बिदु का x-निर्देशांक या भुज कहलाता है। किसी बिदु की x-अक्ष से दूरी, उस बिदु का y-निर्देशांक या कोटि कहलाता है।
x-अक्ष पर स्थित किसी बिंदु के निर्देशांक (x, 0) के रूप के होते हैं तथा y-अक्ष पर स्थित किसी बिदु के निर्देशांक (0, y) के रूप के होते हैं।
निर्देशांक ज्यामिति में मूल बिंदु
निर्देशांक (0, 0), अक्ष तल को चार भागों में विभक्त कर देती है जो चतुर्थांश कहलाते हैं। अक्षों के प्रतिच्छेद बिंदु को मूलबिंदु कहते हैं। किसी बिंदु का भुज या x-निर्देशांक उसकी y- अक्ष से दूरी होती है तथा किसी बिंदु की कोटि या y-निर्देशांक उसकी x – अक्ष से दूरी होती है।
दो बिंदुओं के बीच की दूरी का सूत्र
दो बिन्दुओं P और Q के बीच की दूरी उन दो बिन्दुओं को जोड़ने वाले रेखाखण्ड की लम्बाई होती है। या PQ= √{(x₂ – X₁)² + (Y₂ – y₁)²} इसे दूरी सूत्र कहते हैं।
नोट:
ध्यान दें कि चूँकि दूरी सदैव ऋणेतर होती है, हम केवल धनात्मक वर्गमूल लेते हैं।
निर्देशांक ज्यामिति के उपयोग
वस्तुतः, आकृतियों की ज्यामिति का अध्ययन करने के लिए, निर्देशांक ज्यामिति एक बीजीय साधन के रूप में विकसित की गई है। यह बीजगणित का प्रयोग करके ज्यामिति का अध्ययन करने में सहायता करती है तथा बीजगणित को ज्यामिति द्वारा समझने में भी सहायक होती है। इसी कारण, निर्देशांक ज्यामिति के विभिन्न क्षेत्रों में व्यापक अनुप्रयोग हैं, जैसे भौतिकी, इंजीनियरिग, समुद्री-परिवहन (या नौ-गमन), भूकंप शास्त्र संबंधी और कला।
स्मरणीय तथ्य:
P(x₁, y₁) और Q(x₂, y₂) के बीच की दूरी PQ= √{(x₂ – x₁)² + (y₂ – y₁)²} है।
बिदु P(x, y) की मूलबिंदु से दूरी √(x² + y²) होती है।
विभाजन सूत्र
समतल में स्थित दो बिन्दुओं को तीसरा बिन्दु जिस अनुपात में विभाजित करता है उसे विभाजन सूत्र कहते हैं। यह विभाजन दो प्रकार का होता है अन्त: विभाजन और बाह्य विभाजन।
अन्त: विभाजन
किन्हीं दो बिंदुओं A(x₁, y₁) और B (x₂, y₂) पर विचार कीजिए और मान लीजिए बिंदु P(x, y) रेखाखंड AB को m₁ : m₂ के अनुपात में आंतरिक रूप से विभाजित करता है, अर्थात्
PA/PB = m₁ / m₂ है।
x-अक्ष पर AR, PS और BT लंब खींचिए। x-अक्ष के समांतर AQ और PC खींचिए। तब AA समरूपता कसौटी से,
∆ PAQ ~ ∆ BPC
अतः PA/BP = AQ/PC =PQ/BC (1)
अब AQ = RS = OS – OR = x – x₁
PC = ST = OT – OS = x₂ – x
PQ = PS – QS = PS – AR = y – y₁
BC = BT – CT = BT – PS = y₂ – y
इन मानों को (1) में प्रतिस्थापित करने पर, हमें प्राप्त होता हैः
m₁ / m₂ = (x – x₁)/ (x₂ – x) = (y – y₁)/( y₂ – y)
m₁ / m₂ = (x – x₁)/ (x₂ – x) लेने पर x = (m₁ x₂ + m₂ x₁)/ (m₁ + m₂) प्राप्त होता है।
इसी प्रकार m₁ / m₂ = (y – y₁)/( y₂ – y) लेने पर y = (m₁ y₂ + m₂ y₁)/ (m₁ + m₂) प्राप्त होता है।
अतः, दो बिंदुओं A(x₁, y₁) और B (x₂, y₂) को जोड़ने वाले रेखाखंड AB को m₁ : m₂ के अनुपात में आंतरिक रूप से विभाजित करने वाले बिंदु P(x, y) के निर्देशांक हैं:
{(m₁ x₂ + m₂ x₁)/ (m₁ + m₂), (m₁ y₂ + m₂ y₁)/ (m₁ + m₂)}
उपरोक्त को विभाजन सूत्र कहते हैं।
विशिष्ट स्थिति
एक रेखाखंड का मध्य-बिंदु उसे 1 : 1 के अनुपात में विभाजित करता है।
अतः, बिंदुओं A(x₁, y₁) और B (x₂, y₂) को जोड़ने वाले रेखाखंड AB के मध्य-बिंदु के निर्देशांक
{(1 × x₂ + 1 × x₁)/ (1 + 1), (1 × y₂ + 1 × y₁)/ (1 + 1)}
{(x₂ + x₁)/2, (y₂ + y₁)/2} होंगे।
Example:
उस बिंदु के निर्देशांक ज्ञात कीजिए जो बिंदुओं (4, – 3) और (8, 5) को जोड़ने वाले रेखाखंड को आंतरिक रूप से 3 : 1 के अनुपात में विभाजित करता है।
हल
मान लीजिए P(x, y) वांछित बिंदु है। विभाजन सूत्र का प्रयोग करने पर हमें
x = {3(8) + 1(4)}/(3 + 1) = 7,
y = {3(5) + 1(-3)}/(3 + 1) = 3 प्राप्त होते हैं।
अतः (7, 3) ही वांछित बिंदु है।
त्रिभुज का क्षेत्रफल
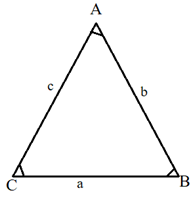
मान लीजिए ABC एक त्रिभुज है, जिसके शीर्ष A(x₁, y₁), B(x₂, y₂) और C(x₃, y₃) हैं। क्रमशः बिदुओं A, B और C से x-अक्ष पर लंब AP, BQ और CR खींचिए। स्पष्टतः चतुर्भुज ABQP, APRC और BQRC समलंब हैं।
∆ ABC का क्षेत्रफल = समलंब ABQP का क्षेत्रफल + समलंब APRC का क्षेत्रफल – समलंब BQRC का क्षेत्रफल
आप यह भी जानते हैं कि एक समलंब का क्षेत्रफल = ½ (समांतर भुजाओं का योग) × (उनके बीच की दूरी)
अतः ∆ ABC का क्षेत्रफल = 1/2(BQ + AP) × QP + 1/2(AP + CR) × PR – 1/2(BQ + CR) × QR
= ½ (y₂ + y₁) (x₁ – x₂) + ½ (y₁ + y₃) (x₃ – x₁) – ½ (y₂ + y₃) (x₃ – x₂)
= ½ [x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃( y₁ – y₂)]
अतः ∆ ABC का क्षेत्रफल व्यंजक = ½ [ x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] का संख्यात्मक मान है।
उदाहरण
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (1, -1), (- 4, 6) और (-3, -5) है।
हल
शीर्षों A(1, -1), B(- 4, 6) और C(-3, -5) वाले त्रिभुज ABC का क्षेत्रफल, उपरोक्त सूत्र द्वारा निम्नलिखित हैः
= ½ [ 1(6 + 5) + (-4)(-5 + 1) + (-3)( -1- 6)]
= ½ (11 + 16 + 21)
= 24
अतः त्रिभुज का क्षेत्रफल 24 वर्ग मात्रक है।
नोट:
क्षेत्रफल एक माप है, इसलिए यह ऋणात्मक नहीं हो सकता है।
उदाहरण
k का मान ज्ञात कीजिए, यदि बिदु A(2, 3), B(4, k) और C(6, -3) संरेखी हैं।
हल
चूँकि तीनों बिदु संरेखी हैं, इसलिए इनसे बनने वाले त्रिभुज का क्षेत्रफल 0 होगा।
अर्थात्
½ [ 2(k + 3) + 4(-3 – 3) + 6(3 – k)] = 0
या ½ (- 4k) = 0
या k = 0
अतः k का वांछित मान 0 है।
उत्तर की जांच के लिए ∆ ABC का क्षेत्रफल = ½ [ 2(0 + 3) + 4(-3 – 3) + 6(3 – 0)]
= ½ (6 – 24 + 18)
= 0
त्रिभुज की सहायता से बहुभुज का क्षेत्रफल ज्ञात करना
किसी बहुभुज का क्षेत्रफल ज्ञात करने के लिए, हम उसे ऐसे त्रिभुजों में बाँटते हैं, जिनमें कोई क्षेत्र सार्वनिष्ठ न हो और फिर इन सभी त्रिभुजों के क्षेत्रफलों को जोड़ लेते हैं।
उदाहरण
यदि A(–5, 7), B(– 4, –5), C(–1, –6) और D(4, 5) एक चतुर्भुज ABCD के शीर्ष हैं, तो इस चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हल
B को D से मिलाने पर, आपको दो त्रिभुज ABD और BCD प्राप्त होते हैं।
अब त्रिभुज ABD का क्षेत्रफल = ½ [ -5(-5 – 5) + (-4)(5 – 7) + 4(7 + 5)]
= ½ (50 + 8 + 48)
= 53 वर्ग मात्रक
साथ ही त्रिभुज BCD का क्षेत्रफल = ½ [ -4(-6 – 5) – 1(5 + 5) + 4(-5 + 6)]
= ½ (44 – 10 + 4)
= 19 वर्ग मात्रक
अतः चतुर्भुज ABCD का क्षेत्रफल = त्रिभुज ABD का क्षेत्रफल + त्रिभुज BCD का क्षेत्रफल
= 53 + 19 = 72 वर्ग मात्रक
मान लीजिए A(4, 2), B[6, 5) और C(1, 4) एक त्रिभुज ABC के शीर्ष हैं।
(i) A से होकर जाने वाली मध्यिका BC से D पर मिलती है। बिंदु D के निर्देशांक ज्ञात कीजिए।
(ii) AD पर स्थित ऐसे बिंदु P के निर्देशांक ज्ञात कीजिए कि AP:PD = 2:1 हो।
(iii) मध्यिकाओं BE और CF पर ऐसे बिंदुओं Q और R के निर्देशांक ज्ञात कीजिए कि BQ:QE = 2:1 हो और CR:RF = 2:1 हो।
आप क्या देखते है?
(i) A से होकर जाने वाली मध्यिका BC से D पर मिलती है। इसलिए BC का मध्य बिंदु D है।
बिंदु P के निर्देशांक = {(6+1)/2, (5+4)/2) = (7/2, 9/2)
(ii) AD पर स्थित बिंदु P इसप्रकार है कि AP:PD = 2:1 हो। बिंदु P के निर्देशांक = {(2×7/2 + 1×4)/(2 + 1), (2×9/2 + 1×2)/(2 + 1)} = (11/3, 11/3)
(iii) B से होकर जाने वाली मध्यिका AC से E पर मिलती है। इसलिए AC का मध्य बिंदु E है।
बिंदु E के निर्देशांक = {(4+1)/2, (2+4)/2} = (5/2, 3)
AE पर स्थित बिंदुए इस प्रकार है कि AQ: QE = 2:1 हो।
बिंदु Q के निर्देशांक = (2×5/2+1×6)/(2 + 1), (2×3+1×5)/(2 + 1) = (11/3, 11/3)
C से होकर जाने वाली मध्यिका AB से F पर मिलती है। इसलिए AB का मध्य बिंदु F है।
बिंदु F के निर्देशांक = (4+6)/2, (2+5)/2 = (5, 7/2)
CF पर स्थित बिंदु R इसप्रकार है कि CR: RF = 2:1 हो। बिंदु R के निर्देशांक =
{(2×5+ 1 x 1)/(2 + 1), (2×7/2 + 1×4)/(2 + 1)} = (11/3, 11/3)
(iv) P, Q और R तीनों बिंदुओं के निर्देशांक समान हैं।
स्मरणीय तथ्य
त्रिभुज ABC जिसके शीर्ष A(x₁, y₁), B(x₂, y₂) और C(x₃, y₃) हैं का क्षेत्रफल = ½ [ x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] का संख्यात्मक मान है।
We hope that class 10 Math Chapter 7 निर्देशांक ज्यामिति (Coordinate Geometry) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 7 निर्देशांक ज्यामिति (Coordinate Geometry) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…