पाठ – 8
त्रिकोणमिति का परिचय
In this post we have given the detailed notes of class 10 Math chapter 8 Introduction to Trigonometry in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 8 त्रिकोणमिति का परिचय के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 8 |
| Chapter Name | त्रिकोणमिति का परिचय (Introduction to Trigonometry) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 8 त्रिकोणमिति का परिचय
त्रिकोणमितीय अनुपात
एक समकोण त्रिभुज की भुजाओं के कुछ अनुपातों का उसके न्यून कोणों के सापेक्ष अध्ययन करेंगे जिन्हें कोणों के त्रिकोणमितीय अनुपात कहते हैं। यहाँ हम 0° और 90° के माप वाले कोणों के त्रिकोणमितीय अनुपातों को भी परिभाषित करेंगे।
त्रिकोणमिति का परिचय [Introduction of Trigonometry]
- त्रिकोणमिति गणित की एक अहम शाखा है, जिसके अंतर्गत समकोण त्रिभुज की भुजाओं और कोणों के बीच के सम्बन्धों का का अध्ययन किया जाता है।
- अंग्रेजी शब्द ‘Trigonometry’ की व्युत्पत्ति ग्रीक भाषा के तीन शब्दों से मिलकर हुई है –
‘tri’ (तीन), ‘gon’ (भुजा) और ‘metron’ (माप) अर्थात ‘तीन भुजाओं की माप’ जोकि एक त्रिभुज होता है।
- प्राचीनकाल में त्रिकोणमिति पर मिस्र और बेबीलोन देशों ने कार्य किया है।
- समकोण त्रिभुज (right angled triangle) – ऐसा त्रिभुज जिसमें कोई भी एक कोण 90° का हो।
- न्यूनकोण (acute angle) – 90° से कम मान वाले कोण को न्यूनकोण कहते हैं।
- त्रिकोणमितीय अनुपात (trigonometric ratios)
sin A = लंब/कर्ण या 1/cosec A
cos A = आधार/कर्ण या 1/sec A
tan A = लंब/आधार या 1/cot A
cosec A = कर्ण/लंब या 1/sin A
sec A = कर्ण/आधार या 1/cos A
cot A = आधार/लंब या 1/tan A
ध्यान दें – cosec A, sec A और cot A के अनुपात क्रमशः sin A, cos A और tan A के व्युत्क्रम (उल्टे) होते हैं।
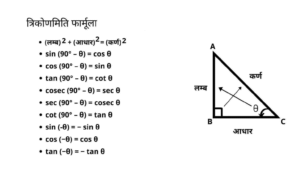
पाईथागोरस प्रमेय से,
(लम्ब)2 + (आधार)2 = (कर्ण)2
अर्थात, (h)2 = (p)2 + (b)2
त्रिकोणमितिय अनुपात के परिचय
Sine = Sin
Tangent = Tan
Cosine = Cos
Cotangent = Cot
Secant = Sec
Cosecant = Cosec
Sin θ | लम्ब / कर्ण = p / h |
Cos θ | आधार / कर्ण = b / h |
Tan θ | लम्ब / आधार = p / b |
Cot θ | आधार / लम्ब = b / p |
Sec θ | कर्ण / आधार = h / b |
Cosec θ | कर्ण / लम्ब = h / p |
त्रिकोणमितिय अनुपातो के बिच सम्बन्ध
- sinθ × Cosecθ = 1
- sinθ = 1 / Cosecθ
- Cosecθ = 1 / sinθ
- Cosθ × Secθ = 1
- Cosθ = 1 / Secθ
- Secθ = 1 / Cosθ
- Tanθ × Cotθ = 1
- Tanθ = 1 / Cotθ
- Cotθ = 1 / Tanθ
- Tanθ = sinθ / Cosθ
- Cotθ = Cosθ / sinθ
महत्वपूर्ण त्रिकोणमितीय अनुपात:
- sin A = लंब/कर्ण या 1/cosec A
- cos A = आधार/कर्ण या 1/sec A
- tan A = लंब/आधार या 1/cot A
- cosec A = कर्ण/लंब या 1/sin A
- sec A = कर्ण/आधार या 1/cos A
- cot A = आधार/लंब या 1/tan A
ध्यान देनें योग्य बातें
अनुपात cosec A, sec A और cot A अनुपातों sin A, cos A तथा tan A के व्युत्क्रम होते हैं।
- tan A = लंब/आधार या sin A /cos A
- cosec A = कर्ण/लंब या 1/sin A
- sec A = कर्ण/आधार या 1/cos A
- cot A = आधार/लंब या cos A /cot A
नोट:
यदि कोण समान बना रहता हो, तो एक कोण के त्रिकोणमितीय अनुपातों के मानों में त्रिभुज की भुजाओं की लंबाइयों के साथ कोई परिवर्तन नहीं होता।
टिप्पणी:
क्योंकि समकोण त्रिभुज का कर्ण, त्रिभुज की सबसे लंबी भुजा होता है, इसलिए sin A या cos A का मान सदा ही 1 से कम होता है (या विशेष स्थिति में 1 के बराबर होता है।)
उदाहरण
यदि tan A = 4/3, तो कोण A के अन्य त्रिकोणमितीय अनुपात ज्ञात कीजिए।
हल
आइए सबसे पहले हम एक समकोण ∆ ABC खींचें।
अब, हम जानते हैं कि tan A = लम्ब /आधार = BC /AB = 4/3
अतः यदि BC = 4k, तब AB = 3k जहाँ k धन संख्या है।
अब पाइथागोरस प्रमेय लागू करने पर हमें यह प्राप्त होता है।
AC² = AB² + BC² = (4k)² + (3k)² = 25k²
इसलिए, AC = 5k
अब हम इनकी परिभाषाओं की सहायता से सभी त्रिकोणमितीय अनुपात लिख सकते हैं।
- sin A = लंब/कर्ण = BC/AC = 4k/5k = 4/5
- cos A = आधार/कर्ण = AB/AC = 3k/5k = 3/5
- tan A = लंब/आधार = BC/AB = 4k/3k = 4/3
- cosec A = कर्ण/लंब = AC/BC = 5k/4k = 5/4
- sec A = कर्ण/आधार = AC/AB = 5k/3k = 5/3
- cot A = आधार/लंब = AB/BC = 3k/4k = ¾
कुछ विशिष्ट कोणों के त्रिकोणमितीय अनुपात
ज्यामिति के अध्ययन से आप 30°, 45°, 60° और 90° के कोणों की रचना से आप अच्छी तरह से परिचित हैं। इस अनुच्छेद में हम इन कोणों और साथ ही 0° वाले कोण के त्रिकोणमितीय अनुपातों के मान ज्ञात करेंगे।
45° के त्रिकोणमितीय अनुपात
∆ ABC में, जिसका कोण B समकोण है, यदि एक कोण 45° का हो, तो अन्य कोण भी 45° का होगा अर्थात्
∠ A = ∠ C = 45°
अतः BC = AB
मान लीजिये BC = AB = a
तब पाइथागोरस प्रमेय के अनुसार AC² = AB² + BC² = a² + a² = 2a²
⟹ AC = a√2
त्रिकोणमितीय अनुपातों की परिभाषाओं को लागू करने पर हमें यह प्राप्त होता है:
sin 45° = BC/AC = a/a√2 = 1/√2
cos 45° = AB/AC = a/a√2 = 1/√2
tan 45° = BC/AB = a/a = 1
cot 45° = AB/BC = a/a = 1
cosec 45° = AC/BC = a√2/a = √2
sec 45° = AC/AB = a√2/a = √2
30° और 60° के त्रिकोणमितीय अनुपात
अब हम 30° और 60° के त्रिकोणमितीय अनुपात परिकलित करें। एक समबाहु त्रिभुज ABC पर विचार करें। क्योंकि समबाहु त्रिभुज का प्रत्येक कोण, 60° का होता है, इसलिए ∠A = ∠B = ∠C = 60°
A से भुजा BC पर लंब AD डालिए
अब ∆ ABD ≅ ∆ ACD (क्यों?)
इसलिए, BD = DC
और ∠ BAD = ∠ CAD (CPCT)
अब आप यह देख सकते हैं किः
∆ ABD एक समकोण त्रिभुज है जिसका कोण D समकोण है, और जहाँ ∠ BAD = 30° और ∠ ABD = 60°
त्रिकोणमितीय अनुपातों को ज्ञात करने के लिए हमें त्रिभुज की भुजाओं की लंबाइयाँ ज्ञात करने की आवश्यकता होती है। आइए, हम यह मान लें कि AB = 2a
तब BD = ½ BC = a
और AD² = AB² – BD² = (2a)² – (a)² = 3a²
इसलिए, AD = a√3
अब sin 30° = BD/AB = a/2a = 1/2
cos 30° = AD/AB = a√3/2a = √3/2
tan 30° = BD/AD = a/a√3 = 1/√3
cot 30° = BD/AB = a√3/a = √3
cosec 30° = AB/BD = 2a/a = 2
sec 30° = BD/AB = 2a/a√3 = 2/√3
इसी प्रकार
sin 60° = AD/AB = a√3/2a = √3/2
cos 60° = 1/2
tan 60° = √3
cot 60° = 1/√3
cosec 60° = 2/√3
sec 60° = 2
0° और 90° के त्रिकोणमितीय अनुपात
प्रथम स्थिति 0° के लिए:
यदि समकोण त्रिभुज ABC के कोण A को तब तक और छोटा किया जाए जब तक कि यह शून्य नहीं हो जाता है, तब इस स्थिति में कोण A के त्रिकोणमितीय अनुपातों पर क्या प्रभाव पड़ता है। जैसे-जैसे ∠A छोटा होता जाता है, वैसे-वैसे भुजा BC की लंबाई कम होती जाती है। बिदु C, बिदु B के निकट आता जाता है और अंत में, जब ∠A, 0° के काफी निकट हो जाता है तब AC लगभग वही हो जाता है जो कि AB है।
तब sin A = BC/AC = 0 (क्योंकि BC का मान 0 के निकट होता है)
cos A = AB/AC = 1 (क्योंकि AC = AB)
इस प्रकार ∠A = 0°
sin 0° = 0
cos 0° = 1
tan 0° = 0
cot 0° = 1/0 (परिभाषित नहीं है)
cosec 0° = (परिभाषित नहीं है)
sec 0° = 1
द्वितीय स्थिति 90° के लिए
उस स्थिति में देखें कि ∠A के त्रिकोणमितीय अनुपातों के साथ क्या होता है जबकि ∆ ABC के इस कोण को तब तक बड़ा किया जाता है, जब तक कि 90° का नहीं हो जाता। ∠A जैसे-जैसे बड़ा होता जाता है, ∠C वैसे-वैसे छोटा होता जाता है। अतः ऊपर वाली स्थिति की भाँति भुजा AB की लंबाई कम होती जाती है। बिदु A, बिदु B के निकट होता जाता है और, अंत में जब ∠A, 90° के अत्यधिक निकट आ जाता है, तो ∠C, 0° के अत्यधिक निकट आ जाता है और भुजा AC भुजा BC के साथ लगभग संपाती हो जाती है।
जब ∠C, 0° के अत्यधिक निकट होता है तो ∠A, 90° के अत्यधिक निकट हो जाता है और भुजा AC लगभग वही हो जाती है, जो भुजा BC है। अतः sin A, 1 के अत्यधिक निकट हो जाता है और, जब ∠A, 90° के अत्यधिक निकट होता है, तब ∠C, 0° के अत्यधिक निकट हो जाता है और भुजा AB लगभग शून्य हो जाती है। अतः cos A, 0 के अत्यधिक निकट हो जाता है।
परिभाषा
अतः हम परिभाषित करते हैं:
sin 90° = 1
cos 90° = 0
इनसे अन्य अनुपात भी ज्ञात किये जा सकते है।
tan 90° = परिभाषित नहीं है
cot 90° = 0
cosec 90° = 1
sec 90° = परिभाषित नहीं है
अतिरिक्त टिप्पणी
उपर्युक्त सारणी से आप देख सकते हैं कि जैसे-जैसे ∠A का मान 0° से 90° तक बढ़ता जाता है, sin A का मान 0 से बढ़कर 1 हो जाता है और cos A का मान 1 से घटकर 0 हो जाता है।
पूरक कोण
दो कोणों को पूरक कोण तब कहा जाता है जबकि उनका योग 90° के बराबर होता है। एक समकोण ∆ ABC में यदि कोण B समकोण है तो ∠A + ∠C = 90° होगा।
इसलिए, ∠C = 90° – ∠A
∠A + ∠C को पूरक कोणों का युग्म कहा जाता है।
समकोण ∆ ABC में AB आधार है, BC लम्ब है तथा AC कर्ण है।
अतः
- sin A = लंब/कर्ण = BC/AC
- cos A = आधार/कर्ण = AB/AC
- tan A = लंब/आधार = BC/AB
- cosec A = कर्ण/लंब = AC/BC
- sec A = कर्ण/आधार = AC/AB
- cot A = आधार/लंब = AB/BC
पूरक कोणों के त्रिकोणमितीय अनुपात
आइए, अब हम ∠C = 90° – ∠A के त्रिकोणमितीय अनुपात लिखेते हैं।
सुविधा के लिए हम 90° – ∠A के स्थान पर 90° – A लिखेंगे।
कोण 90° – A की सम्मुख भुजा और संलग्न भुजा क्या होगी?
आप देखेंगे कि AB कोण 90° – A की सम्मुख भुजा है और BC संलग्न भुजा है। अतः
- sin (90° – A) = लंब/कर्ण = AB/AC
- cos (90° – A) = आधार/कर्ण = BC/AC
- tan (90° – A) = लंब/आधार = AB/BC
- cot (90° – A) = आधार/लम्ब = BC/AB
- cosec (90° – A) = कर्ण/लम्ब = AC/AB
- sec (90° – A) = कर्ण/आधार = AC/BC
अनुपातों कि तुलना
उपरोक्त दोनों अनुपातों कि तुलना करने पर हम पाते हैं कि
- sin (90° – A) = AB/AC = cos A
- cos (90° – A) = BC/AC = sin A
- tan (90° – A) = AB/BC = cot A
- cot (90° – A) = BC/AB = tan A
- cosec (90° – A) = AC/AB = sec A
- sec (90° – A) = AC/BC = cosec A
त्रिकोणमितीय सर्वसमिकाएँ
एक समीकरण को एक सर्वसमिका तब कहा जाता है जबकि यह संबंधित चरों के सभी मानों के लिए सत्य हो। इसी प्रकार एक कोण के त्रिकोणमितीय अनुपातों से संबंधित सर्वसमिका को त्रिकोणमितीय सर्वसमिका कहा जाता है। जबकि यह संबंधित कोण (कोणों) के सभी मानों के लिए सत्य होता है।
- cos² A + sin² A = 1 (जहाँ 0° ≤ A ≤ 90°)
- 1 + tan² A = sec² A
- cot² A + 1 = cosec² A
स्मरणीय तथ्य
यदि एक न्यून कोण का एक त्रिकोणमितीय अनुपात ज्ञात हो, तो कोण के शेष त्रिकोणमितीय अनुपात सरलता से ज्ञात किए जा सकते हैं।
sin A या cos A का मान कभी भी 1 से अधिक नहीं होता, जबकि sec A या cosec A का मान सदैव 1 से अधिक या 1 के बराबर होता है।
- sin और cos में सम्बन्ध –
tan A = sin A/cos A
cot A = cos A/sin A
- त्रिकोणमितीय अनुपातों के नाम पूर्ण रूप में –
sin – sine
cos – cosine
tan – tangent
cosec – cosecant
sec – secant
cot – cotangent
- ध्यान रहे कि tan A, tan और A का गुणनफल नहीं है। tan का A से अलग हो जाने पर कोई मान नहीं रहता। इसी प्रकार अन्य त्रिकोणमितीय अनुपातों के साथ भी होता है।
- पूर्ण रूप से समरूप त्रिभुजों के त्रिकोणमितीय अनुपातों में कोई अंतर नहीं होता है।
- कोण को दर्शाने के लिए हम English Alphabet के किसी Letter का प्रयोग करते हैं और कभी-कभी ग्रीक अक्षर थीटा (theta) का प्रयोग करते हैं।
- किसी भी समकोण त्रिभुज की दो भुजाएँ या उनका अनुपात दिए होने पर हम तीसरी भुजा पाइथागोरस प्रमेय के द्वारा ज्ञात कर सकते हैं और फिर सभी त्रिकोणमितीय अनुपात भी ज्ञात कर सकते हैं।
- निम्न सारणी त्रिकोणमिति के 0°, 30°, 45°, 60° और 90° के अनुपातों को दर्शाती है –
त्रिकोणमिति तालिका :Trigonometry Table
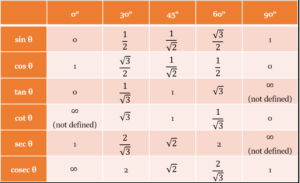
- किसी समकोण त्रिभुज की कोई एक भुजा और एक न्यूनकोण दिए होने हम अन्य दो भुजाएँ, कोण का त्रिकोणमितीय मान रखकर ज्ञात कर सकते हैं, और फिर सभी त्रिकोणमितीय अनुपात भी ज्ञात कर सकते हैं।
- किसी समकोण त्रिभुज की दो या तीनों भुजाएँ दी होने पर त्रिभुज के कोण ज्ञात किये जा सकते हैं, यदि भुजाओं का अनुपात किसी भी कोण के त्रिकोणमितीय अनुपात के बराबर आता है।
- त्रिकोणमितीय प्रश्नों को हल करते समय ध्यान रखें कि सर्वप्रथम अनुपातों को सम्बन्धित सूत्र/अनुपात में परिवर्तित करे ताकि हल करने में आसानी हो जाए।
- पूरक कोणों के त्रिकोणमितीय अनुपात
sin (90°-A) = cos A
cos (90°-A) = sin A
tan (90°-A) = cot A
cot (90°-A) = tan A
cosec (90°-A) = sec A
sec (90°-A) = cosec A
त्रिकोणमितीय सर्वसमिकाएँ
- sin2 A + cos2 A = 1
- sec2 A + tan2 A = 1
- cosec2 A – cot2 A = 1
- कोई भी त्रिकोणमितीय अनुपात दिया होने पर हम त्रिकोणमितीय सर्वसमिकाओं (identities) की सहायता से अन्य त्रिकोणमितीय अनुपात ज्ञात कर सकते हैं।
- त्रिकोणमितीय प्रश्नों को हल करते समय यदि किसी किसी प्रश्न या उसके हल में कहीं भी कोई सर्वसमिका लागू होती है तो, उसमें सर्वसमिका अवश्य लगाएँ।
- यदि त्रिकोणमिति के किसी प्रश्न में दो पक्षों को सत्यापित (prove) करने के लिए कहा जाए तो पहले बड़े पक्ष को हल करें और छोटे पक्ष के बराबर लाने का प्रयत्न करें। यदि पक्ष बराबर नहीं आते तो बड़े पक्ष को अधिकतम सीमा तक सरल (simplify) करने के बाद छोटे पक्ष को भी सरल करें, आपका उत्तर अवश्य सही होगा।
- दाएँ पक्ष के किसी धनात्मक पद को बाईं तरफ विस्थापित करने पर उसका चिन्ह ऋणात्मक हो जाता है। विलोमशः भी सत्य है।
त्रिकोणमितीय अनुपातों के चिन्ह विभिन्न कोटि में
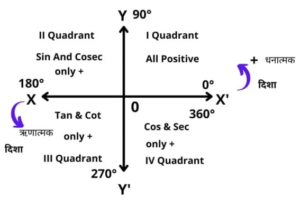
- चतुर्थांश में केवल 90° और 270° चेंज होते है शेष नही बदलते है.
- प्रथम चतुर्थांश में सभी त्रिकोणमितिय अनुपात धनात्मक होते है.
- द्वितीय चतुर्थांश में केवल Sin और Cosec धनात्मक होते है शेष ऋणात्मक होते है.
- तृतीय चतुर्थांश में Tan और Cot धनात्मक, शेष ऋणात्मक
- चतुर्थ चतुर्थांश में, Cos और Sec धनात्मक, शेष ऋणात्मक
- कोण की चाल घड़ी के विपरीत दिशा में पॉजिटिव एवं घड़ी के दिशा में नेगेटिव होता है.
प्रथम चतुर्थांश में (θ – 90°), सभी पॉजिटिव
- sin (90° – θ) = cos θ
- cos (90° – θ) = sin θ
- tan (90° – θ) = cot θ
- cosec (90° – θ) = sec θ
- sec (90° – θ) = cosec θ
- cot (90° – θ) = tan θ
प्रथम चतुर्थांश में ही (360° + θ)
- sin (360° + θ) = sin θ
- cos (360° + θ) = cos θ
- tan (360° + θ) = tan θ
- cosec (360° + θ) = cosec θ
- sec (360° + θ) = sec θ
- cot (360° + θ) = cot θ
द्वितीय चतुर्थांश में (90° – 180°), Sin और Cosec Positive
- sin (180° – θ) = sin θ
- cos (180° – θ) = – cos θ
- tan (180° – θ) = – tan θ
- cosec (180° – θ) = cosec θ
- sec (180° – θ) = – sec θ
- cot (180° – θ) = – cot θ
द्वितीय चतुर्थांश में (90° + θ)
- sin (90° + θ) = cos θ
- cos (90° + θ) = – sin θ
- tan (90° + θ) = – cot θ
- cosec (90° + θ) = sec θ
- sec (90° + θ) = – cosec θ
- cot (90° + θ) = – tan θ
तृतीय चतुर्थांश में (180° – 270°), Tan और Cot पॉजिटिव
- sin (180° + θ) = – sin θ
- cos (180° + θ) = – cos θ
- tan (180° + θ) = tan θ
- cosec (180° + θ) = – cosec θ
- sec (180° + θ) = – sec θ
- cot (180° + θ) = cot θ
तृतीय चतुर्थांश में (270° – θ)
- sin (270° – θ) = – cos θ
- cos (270° – θ) = – sin θ
- tan (270° – θ) = cot θ
- cosec (270° – θ) = – sec θ
- sec (270° – θ) = – cosec θ
- cot (270° – θ) = tan θ
चतुर्थ चतुर्थांश में (270° – 360°), Cos और Sec पॉजिटिव
- sin (360° – θ) = – sin θ
- cos (360° – θ) = cos θ
- tan (360° – θ) = – tan θ
- cosec (360° – θ) = – cosec θ
- sec (360° – θ) = sec θ
- cot (360° – θ) = – cot θ
चतुर्थ चतुर्थांश में (270° + θ)
- sin (270° + θ) = – cos θ
- cos (270° + θ) = + sin θ
- tan (270° + θ) = – cot θ
- cosec (270° + θ) = – sec θ
- sec (270° + θ) = + cosec θ
- cot (270° + θ) = – tan θ
त्रिकोणमितिय अनुपातों का चिन्ह (Trigonometric Sign)
- sin (-θ) = − sin θ
- cos (−θ) = cos θ
- tan (−θ) = − tan θ
- cosec (−θ) = − cosec θ
- sec (−θ) = sec θ
- cot (−θ) = − cot θ
दो कोणों का योग या घटाव फार्मूला
- sin (A + B) = sin A cos B + cos A sin B
- sin (A − B) = sin A cos B – cos A sin B
- cos (A + B) = cos A cos B – sin A sin B
- cos (A – B) = cos A cos B + sin A sin B
- tan(A – B)= (tan A – tan B) / (1 + tan A . tan B)
- cot(A – B) = (cot A . cot B + 1) / (cot B – cot A)
- tan(A + B) = [(tan A + tan B) / (1 – tan A tan B)]
- tan(A – B) = [(tan A – tan B) / (1 + tan A tan B)]
त्रिकोणमितिय असिमाका (Trigonometric Identitie)
- sin2A + cos2A = 1
- sin²θ = 1 – cos²θ
- cos²θ = sin²θ – 1
- tan2A + 1 = sec2A
- tan²θ = sec²θ – 1
- cot2A + 1 = cosec2A
- cot²θ = cosec²θ – 1
दो कोणों का फार्मूला
- sin(2 A) = 2sin(A) • cos(A)
- cos(2 A) = cos2(A)–sin2(A)
- tan(2 A) = [2 tan(A)] / [1−tan2(A)]
We hope that class 10 Math Chapter 8 त्रिकोणमिति का परिचय (Introduction to Trigonometry) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 8 त्रिकोणमिति का परिचय (Introduction to Trigonometry) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…
Wow very nice