पाठ – 11
रचनाएँ
In this post we have given the detailed notes of class 9 Math chapter 11 Constructions in Hindi. These notes are useful for the students who are going to appear in class 9 board exams.
इस पोस्ट में कक्षा 9 के गणित के पाठ 11 रचनाएँ के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 9 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Math |
| Chapter no. | Chapter 11 |
| Chapter Name | रचनाएँ (Constructions) |
| Category | Class 9 Math Notes in Hindi |
| Medium | Hindi |
पाठ 11, रचनाएँ
आधारभूत रचनाएँ
- इस अध्याय में पटरी और परकार की सहायता से कुछ आधारभूत रचनाएँ करेंगे। जैसे: दिए गए कोण का समद्विभाजन करना, दिए गए रेखाखंड पर समद्विभाजक की रचना तथा त्रिभुजों की रचना करना आदि शामिल हैं।
- एक दिए हुए कोण के समद्विभाजक की रचना करना।
- एक कोण ABC दिया है। हम इसके समद्विभाजक की रचना करना चाहते हैं।
रचना के चरण:
- B को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए जो किरण BA और BC को क्रमशः, मान लीजिए, E और D पर प्रतिच्छेद करता है।
- पुनः D और E को केन्द्र मानकर तथा
 DE से बड़ी त्रिज्या लेकर चाप लगाइए, जो (मान लीजिए) एक दूसरे को F पर प्रतिच्छेद करते हैं।
DE से बड़ी त्रिज्या लेकर चाप लगाइए, जो (मान लीजिए) एक दूसरे को F पर प्रतिच्छेद करते हैं। - किरण BF खींचिए। यही किरण BF कोण ABC का अभीष्ट समद्विभाजक है।
इस तथ्य का परीक्षण करते है कि इस विधि से कोण समद्विभाजक किस प्रकार प्राप्त हुआ है।
DF और EF को मिलाइए। अब त्रिभुजों BEF तथा BDF में,
BE = BD (एक ही चाप की त्रिज्याएँ)
EF = DF (समान त्रिज्या वाले चाप)
BF = BF (उभयनिष्ठ भुजा)
अतः, ∆ BEF ≅ ∆ BDF (SSS नियम)
इससे प्राप्त होता है: ∠EBF = ∠DBF (CPCT)
एक दिए गए रेखाखंड के लम्ब समद्विभाजक (लम्बार्धक) की रचना करना।
एक रेखाखंड AB दिया है। हम इसके लम्ब समद्विभाजक की रचना करना चाहते हैं।
रचना के चरण:
- A और B को केन्द्र मानकर तथा
 AB से अधिक त्रिज्या लेकर रेखाखंड AB के दोनों ओर (एक दूसरे को प्रतिच्छेद करते हुए) चाप लगाइए।
AB से अधिक त्रिज्या लेकर रेखाखंड AB के दोनों ओर (एक दूसरे को प्रतिच्छेद करते हुए) चाप लगाइए। - मान लीजिए कि ये चाप एक दूसरे को P और Q पर प्रतिच्छेद करते हैं। PQ को मिलाइए।
- मान लीजिए PQ, AB को बिन्दु M पर प्रतिच्छेद करती है। तब रेखा PMQ, AB का अभीष्ट लम्ब समद्विभाजक है।
इस तथ्य का परीक्षण करते है कि यह विधि किस प्रकार AB का लम्ब समद्विभाजक देती है।
A और B को P और Q से मिलाइए जिससे AP, AQ, BP तथा BQ प्राप्त होते हैं।
त्रिभुजों PAQ तथा PBQ में,
AP = BP (समान त्रिज्या वाले चाप)
AQ = BQ (समान त्रिज्या वाले चाप)
PQ = PQ (उभनिष्ठ)
अतः ∆PAQ ≅ ∆PBQ (SSS नियम)
इसलिए, ∠APM = ∠BPM (CPCT)
अब त्रिभुजों PAQ तथा PBQ में,
AP =BP (समान त्रिज्या वाले चाप)
PM = PM (उभयनिष्ठ)
∠APM = ∠BPM (ऊपर सिद्ध किया जा चुका है)
अतः ∆PMA ≅ ∆PMB (SAS नियम)
इसलिए, AM = BM तथा ∠PMA = ∠PMB (CPCT नियम)
क्योंकि ∠PMA + ∠PMB = 180° (रैखिक युग्म अभिगृहीत)
हम पाते है:
∠PMA = ∠PMB = 90°
अतः PM, अर्थात् PMQ रेखाखंड AB का लम्ब समद्विभाजक है।
त्रिभुजों की कुछ रचनाएँ
किसी त्रिभुज की रचना के लिए, कम से कम उसके तीन भाग दिए होने चाहिए।
- एक त्रिभुज अद्वितीय होता है, यदि
- दो भुजाएँ और बीच का कोण दिए हों,
- तीनों भुजाएँ दी हों,
- दो कोण और बीच की भुजा दी हो तथा
- समकोण त्रिभुज में कर्ण और एक भुजा दी हो।
दिए हुए आधार, एक आधार कोण तथा अन्य दो भुजाओं के योग से त्रिभुज की रचना करना।
एक त्रिभुज ABC में आधार BC, एक आधार कोण माना ∠B तथा अन्य दो भुजाओं का योग AB + AC दिया है। आपको त्रिभुज ABC की रचना करनी है।
रचना के चरण:
- आधार BC खींचिए और बिन्दु B पर दिए गए कोण के बराबर ∠XBC बनाइए।
- किरण BX से AB + AC के बराबर रेखाखंड BD काटिए।
- DC को मिलाइए तथा ∠BDC के बराबर कोण DCY बनाइए।
- मान लीजिए CY, BX को A पर प्रतिच्छेदित करती है।
तब, ABC अभीष्ट त्रिभुज है।
आइए देखें कि आपने अभीष्ट त्रिभुज कैसे प्राप्त किया।
दिए गए मापन अनुसार, आधार BC तथा ∠B बनाए गए हैं।
पुनः त्रिभुज ACD में,
∠ACD = ∠ADC (रचना से)
अतः AC = AD होगा, और फिर
AB = BD – AD = BD – AC
अर्थात् AB + AC = BD
टिप्पणी:
त्रिभुज की रचना संभव नहीं होगी यदि योग AB + AC ≤ BC हो।
एक त्रिभुज की रचना कीजिए जिसका परिमाप तथा दोनों आधार कोण दिए हों।
आधार के कोण ∠B तथा ∠C और (BC + CA + AB) दिए हैं। आपको त्रिभुज ABC की रचना करनी है।
रचना के चरण:
- BC + CA + AB के बराबर एक रेखाखंड XY, खींचिए।
- ∠LXY कोण B के बराबर तथा ∠MYX कोण C के बराबर बनाइए।
- ∠LXY तथा ∠MYX को समद्विभाजित कीजिए। माना ये समद्विभाजक एक बिन्दु A पर प्रतिच्छेद करते हैं।
- AX का लंब समद्विभाजक PQ तथा AY का लंब समद्विभाजक RS खींचिए।
- मान लीजिए कि PQ, XY को बिंदु B पर तथा RS, XY को बिंदु C पर प्रतिच्छेद करता है। AB और AC को मिलाइए।
तब ABC अभीष्ट त्रिभुज है। रचना के समर्थन के लिए, आप पाते हैं कि B, AX के लंब समद्विभाजक पर स्थित है।
अतः, XB = AB है। इसी प्रकार, CY = AC है।
इससे प्राप्त होता हैः BC + CA + AB = BC + XB + CY = XY
पुनः ∠BAX = ∠AXB (क्योंकि ∆ AXB में AB = XB)
तथा ∠ABC = ∠BAX + ∠AXB = 2 ∠AXB = ∠LXY
इस प्रकार, ∠ACB = ∠MYX, जैसा चाहिए था।
परिभाषा
रेखागणित में ‘रचना’ से तात्पर्य आकृतियों, कोणों और रेखाओं को सही सही बनाने से है।
इन्हें हम परकार, अंशांकित पटरी और पेन्सिल की सहायता से बना सकते हैं।
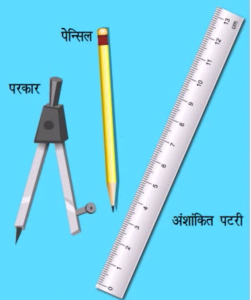
कुछ रचनाओं में, जहाँ माप लेने की भी आवश्यकता होती है, हम अंशांकित पटरी और चांदा का भी प्रयोग कर सकते हैं।
एक दिए गए कोण का समद्विभाजक:
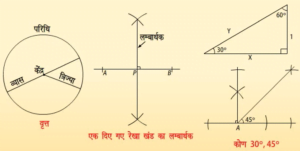
कोण का समद्विभाजक बनाना सीखेंगे। अब हमें इस कोण का समद्विभाजक बनाना है।
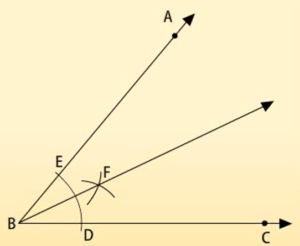
रचना के चरण:
- B को केंद्र मान कर किसी भी त्रिज्या का कोई चाप लगाएंगे जो BA और BC किरणों को क्रमशः E और D पर प्रतिच्छेदित करेगा।
- फिर D को केंद्र मान कर DE की आधी लम्बाई से अधिक की त्रिज्या लेकर हम एक चाप लगाएंगे।
- ठीक इसी तरह E को केन्द्र मान कर DE की आधी लम्बाई से अधिक की त्रिज्या लेकर हम एक और चाप लगाएंगे जो पहले चाप को F पर प्रतिच्छेदित करेगा।
- किरण BF खींचेगे। यही किरण BE,
 ABC की समद्विभाजक है।
ABC की समद्विभाजक है। - हम कैसे कह सकते हैं कि BF एक कोण सम्द्विभाजक है।
DF और EF को मिला दीजिए।
त्रिभुजों BEF और BDF में
BE = BD (चाप की त्रिज्या)
EF = DF (त्रिज्या के चाप)
BF = BF (दोनों)
इसलिए, ![]() BEF
BEF ![]()
![]() BDF (SSS नियम)
BDF (SSS नियम)
जिससे ![]() EBF =
EBF = ![]() DBF (CPCT)
DBF (CPCT)
इसलिए, BF एक कोण द्विभाजक है।
दिए गए रेखाखंड का लम्बार्धक:
दिए गए रेखाखंड के लम्बार्धक की रचना।
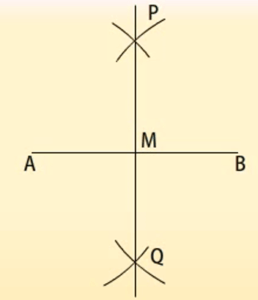
रचना के चरण:
- सबसे पहले A को केंद्र मानकर AB की लम्बाई के आधे से अधिक की त्रिज्या लेकर रेखाखंड AB के दोनों ओर एक एक चाप खींचिए।
- ठीक इसी तरह B को केन्द्र मानकर उसी त्रिज्या के एक एक चाप रेखाखंड AB के दोनों ओर लगाये जो पहले वाले दोनों चाप को क्रमशः P और Q पर प्रतिच्छेदित करेगा।
- PQ को मिला दें।
- PQ, AB को M बिंदु पर प्रतिच्छेदित करेगी। यही रेखा PMQ रेखाखंड AB की अभीष्ट लम्बार्धक है।
- सिद्ध करते हैं कि PMQ रेखाखंड AB का लम्बार्धक है।
A और B को P तथा Q से मिलाकर AP,AQ, BP और BQ बनाइये।
PAQ और PBQ त्रिभुजों मे
AP = BP (बराबर त्रिज्या के चाप)
AQ = BQ (बराबर त्रिज्या के चाप)
PQ = PQ (दोनों)
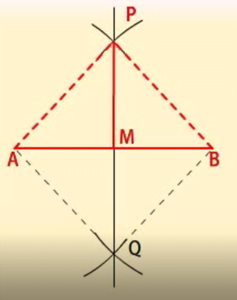
इसलिए, ![]() PAQ
PAQ ![]()
![]() PBQ (SSS नियम)
PBQ (SSS नियम)
इसलिए, ![]() APM =
APM = ![]() BPM (CPCT)
BPM (CPCT)
अब त्रिभुजों PMA और PMB में
AP = BP (बराबर त्रिज्या के चाप)
PM = PM (दोनों)
![]() APM =
APM = ![]() BPM (ऊपर सिद्ध हो चुका है।)
BPM (ऊपर सिद्ध हो चुका है।)
इसलिए, ![]() PMA
PMA ![]()
![]() PMB
PMB
इसलिए, AM = BM और ![]() PMA =
PMA = ![]() PMB (CPCT)
PMB (CPCT)
अतः ![]() PMA +
PMA + ![]() PMB = 180° (रैखिक युग्म अभिगृहीत),
PMB = 180° (रैखिक युग्म अभिगृहीत),
![]() PMA =
PMA = ![]() PMB = 90°
PMB = 90°
इसलिए, PM जो PMQ है, रेखाखंड AB का लम्बार्धक है।
60° का कोण:
किसी दी गयी किरण के प्रारंभिक बिंदु पर 60° के कोण की रचना करना सीखेंगे। हम एक ऐसी किरण AC की रचना करना चाहते हैं जिससे CAB = 60° हो।
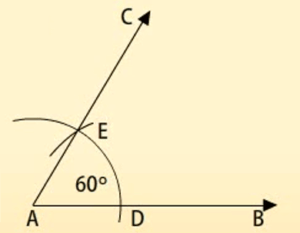
रचना के चरण:
- A को केन्द्र मान कर किसी भी त्रिज्या का एक वृत्त का चाप लगाइए। जो AB को किसी बिंदु पर प्रतिच्छेदित करेगा। माना कि वह बिंदु D है।
- D को केन्द्र मानकर पहले वाली ही त्रिज्या का एक और चाप लगाइए जो पहले वाले चाप को किसी बिंदु पर प्रतिच्छेदित करेगा। माना कि वह बिंदु E है।
- E से होते हुए किरण AC खींचिए।
 CAB, 60° का अभीष्ट कोण है।
CAB, 60° का अभीष्ट कोण है।
हम इस विधि से किस प्रकार 60° का अभीष्ट कोण प्राप्त करते हैं।
तब, AE = AD = DE (रचना के अनुसार)
इसलिए, ![]() EAD एक समबाहु त्रिभुज है। त्रिभुज EAD भी एक समबाहु त्रिभुज है क्योंकि
EAD एक समबाहु त्रिभुज है। त्रिभुज EAD भी एक समबाहु त्रिभुज है क्योंकि ![]() CAB, 60° का है।
CAB, 60° का है।
एक त्रिभुज की रचना:
- दिए गए आधार, एक आधार कोण, तथा अन्य दो भुजाओं के योग की सहायता से त्रिभुज की रचना करना।
- ABC कोई त्रिभुज है BC जिसमें आधार, B एक आधार कोण और AB + AC त्रिभुज ABC की अन्य दो भुजाओं का योग है। हमें त्रिभुज ABC की रचना करनी है।
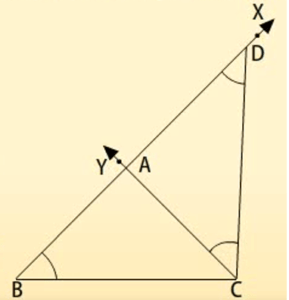
रचना के चरण:
- आधार BC खींचे और बिंदु B पर दिए गए कोण के बराबर एक कोण XBC बनाएँ।
- किरण BX से AB + AC के बराबर एक रेखाखंड BD काटें।
- अब DC को मिला दें और BDC के बराबर एक कोण DCY बनाएँ।
- CY, BX को A पर प्रतिच्छेदित करेगी। ABC हमारा अभीष्ट त्रिभुज है।
आइये देखते हैं कि ABC किस प्रकार एक त्रिभुज है।
ACD त्रिभुज में, LACD = ZADC (रचना के अनुसार)
इसलिए, AC = AD
तब,
AB = BD – AD = BD – AC
AB + AC = BD
हम जानते हैं कि त्रिभुज की दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
इसलिए ABC एक त्रिभुज है।
दिए गए आधार, एक आधार कोण, तथा अन्य दो भुजाओं के अंतर की सहायता से त्रिभुज की रचना करना।
आधार BC, आधार ![]() B, और दो भुजाओं का अंतर दिया गया है।
B, और दो भुजाओं का अंतर दिया गया है।
पहली स्थिति: AB – AC
दूसरी स्थिति: AC – AB
हमें त्रिभुज ABC बनाना है।
पहली स्थिति: जब AB > AC और AB – AC दिया हुआ है
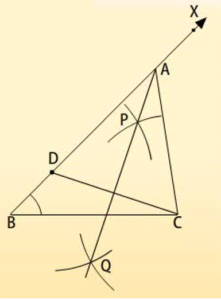
रचना के चरण:
- आधार BC खींचे और बिंदु B पर दिए गए कोण के बराबर एक कोण XBC बनाएँ।
- अब, किरण BX से AB – AC के बराबर एक रेखाखंड BD काटें।
- अगले चरण में DC को मिला दें और DC का लम्बार्धक PQ खींचें।
- इसे BX को एक बिंदु A पर प्रतिच्छेदित करने दें। AC को मिला दें। ABC हमारा अभीष्ट त्रिभुज है।
अब दूसरी स्थिति का प्रयोग करते हुए त्रिभुज बनाते हैं:
जिसमें AB < AC और AC – AB जो दिया गया है-
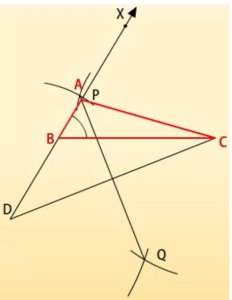
रचना के चरण:
- सबसे पहले आधार BC खींचे और बिंदु B पर दिए गए कोण के बराबर एक कोण XBC बनाएँ।
- अब, किरण BX से AC – AB के बराबर एक रेखाखंड BD काटें।
- DC को मिला दें और DC का लम्बार्धक PQ खींचें।
- PQ को BX को एक बिंदु A पर प्रतिच्छेदित करने दें। AC को मिला दें।
यही ABC हमारा अभीष्ट त्रिभुज है।
दिए गए परिमाप और दो आधार कोणों की सहायता से एक त्रिभुज की रचना करें।
माना की ![]() B और
B और ![]() C दिए गए कोण हैं और BC + CA + AB परिमाप है। हमें एक त्रिभुज ABC की – रचना करनी है
C दिए गए कोण हैं और BC + CA + AB परिमाप है। हमें एक त्रिभुज ABC की – रचना करनी है
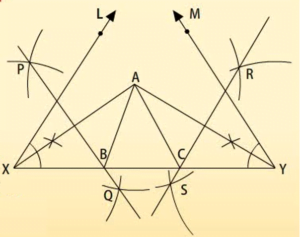
रचना के चरण:
- रेखाखंड XY खींचिए जो BC+ CA + AB के बराबर हो।
- कोण LXY और MYX की रचना कीजिये।
 LYX और
LYX और  MYX को समद्विभाजित कीजिये। ये समद्विभाजक एक दूसरे को बिंदु A पर प्रतिच्छेदित करेंगे।
MYX को समद्विभाजित कीजिये। ये समद्विभाजक एक दूसरे को बिंदु A पर प्रतिच्छेदित करेंगे।- AX और AY के लामबर्धकों PQ और RS की रचना करेंगे।
- PQ, XY को B पर तथा RS, XY को प्रतिच्छेदित करेगा। यही ABC अभीष्ट त्रिभुज है।
उदाहरण:
त्रिभुज ABC की रचना करेंगे, जिसमें ![]() B = 60°,
B = 60°, ![]() C= 30° और AB + BC + CA = 15 cm है।
C= 30° और AB + BC + CA = 15 cm है।
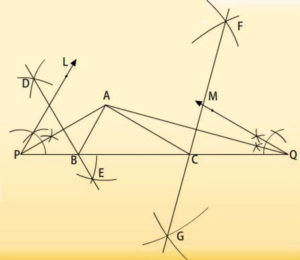
रचना के चरणः
- एक रेखाखंड PQ = 15 cm खींचेंगे जो AB + BC+ CA के बराबर होगा।
- अब P बिंदु पर एक 60° का कोण और Q. बिंदु पर 30° का कोण बनाइये।
- इन कोणों को समद्विभाजित कीजिये। इनके समद्विभाजक एक दूसरे को बिंदु A पर प्रतिच्छेदित करेंगे।
- लम्बार्धकों AP और AQ की रचना करिये जो PQ को क्रमशः B और C पर प्रतिच्छेदित करेंगे।
- अब AB तथा AC को मिला दीजिए। यही ABC अभीष्ट त्रिभुज है।
क्या आप जानते हैं।
- जियोमेट्री शब्द ग्रीक शब्द ‘जीओ’, जिसका तात्पर्य है पृथ्वी, तथा ‘मेट्रिया’, जिसका तात्पर्य है मापना, से बना है।
- अंक गणित के साथ-साथ रेखागणित भी पूर्व-आधुनिक गणित के दो क्षेत्रों में से एक थी।
- प्राचीन मिस्रवासिओं में 3000 ई. पू. पहले रेखागणित का प्रयोग किया था। उनके बहुत सारे सूत्रों में से वृत्त का लगभग सही क्षेत्रफल निकलने का सूत्र भी था।
- अपने अद्भुत रेखा गणितीय कार्यों के कारण रेखागणित का पिता प्रायः 300 ई. पू. के मिस्र के यूक्लिड नाम के गणितज्ञ को कहा जाता है। उसके किये गए कार्यों में इतने प्रभावी ‘तत्व’ थे जो बीसवीं शताब्दी के आरम्भ तक उन गणित की किताबों में रहे, जिनका प्रयोग पढ़ाने के लिए किया जाता था।
- यदि AB + AC < Bc है तो किसी भी त्रिभुज की रचना संभव नहीं है।
सारांश:
आइये हमने जो कुछ सीखा है, उसे संक्षेप में दोहराएं।
- दिए गए कोण को समद्विभाजित करना।
- दिए गए रेखाखंड के लम्बार्धक की रचना करना।
- दिए गए कोण की रचना करना।
- दिए गए आधार, एक आधार कोण, तथा अन्य दो भुजाओं के योग की सहायता से त्रिभुज की रचना करना।
- दिए गए आधार, एक आधार कोण, तथा अन्य दो भुजाओं के अंतर की सहायता से त्रिभुज की रचना करना।
- दिए गए परिमाप और दो आधार कोणों की सहायता से एक त्रिभुज की रचना करना।
We hope that class 9 Math Chapter 11 रचनाएँ (Constructions) Notes in Hindi helped you. If you have any queries about class 9 Math Chapter 11 रचनाएँ (Constructions) Notes in Hindi or about any other Notes of class 9 Math in Hindi, so you can comment below. We will reach you as soon as possible…