पाठ – 13
पृष्ठीय क्षेत्रफल और आयतन
In this post we have given the detailed notes of class 9 Math chapter 13 Surface Areas and Volumes in Hindi. These notes are useful for the students who are going to appear in class 9 board exams.
इस पोस्ट में कक्षा 9 के गणित के पाठ 13 पृष्ठीय क्षेत्रफल और आयतन के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 9 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Math |
| Chapter no. | Chapter 13 |
| Chapter Name | पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes) |
| Category | Class 9 Math Notes in Hindi |
| Medium | Hindi |
पाठ 13, पृष्ठीय क्षेत्रफल और आयतन
पृष्ठीय क्षेत्रफल और आयतन
पृष्ठीय क्षेत्रफल:- पृष्ठीय क्षेत्रफल किसी 3D आकृति पर मौजूद सभी फलकों (या सतहों) के क्षेत्रफल का योग होता है। उदाहरण के लिए घनाभ, घन और बेलनों के पृष्ठीय क्षेत्रफल।
आयतन:- सभी पदार्थ स्थान (त्रि-विमीय स्थान) घेरते हैं। इसी त्रि-विमीय स्थान की मात्रा की माप को आयतन कहते हैं। अर्थात किसी पदार्थ द्वारा घेरे गए लंम्बाई, चौड़ाई और ऊंचाई को व्यक्त करता है।
घनाभ का पृष्ठीय क्षेत्रफल
- छः पृष्ठों से घिरी वह आकृति, जिसमें प्रत्येक पृष्ठ एक आयत होता हैं और सम्मुख पृष्ठ बराबर होते हैं घनाभ कहलाता हैं।
- घनाभ के समस्त पृष्ठों का क्षेत्रफल = 2(लम्बाई × चौड़ाई + चौड़ाई × ऊँचाई + ऊँचाई × लम्बाई)
- घनाभ के सम्पूर्ण पृष्ठ का क्षेत्रफल = 2(lb + bh + hl) वर्ग मात्रक
घन के पृष्ठीय क्षेत्रफल
घन की लम्बाई, चौड़ाई एवं ऊँचाई सामान होती हैं। एक घन में छः फलक, बारह किनारे एवं आठ कोने होते हैं इसके छह बराबर-बराबर आकार के फलक होते हैं हर फलक एक वर्ग होता हैं और छह फलक होने के कारण यह एक प्रकार का षट्फलकी भी कहलाता हैं।
यदि घन का प्रत्येक किनारा या कोर या भुजा a हो, तो उसका पृष्ठीय क्षेत्रफल
= 2(a × a + a × a + a × a) अर्थात् 2 (a² + a² + a²), अर्थात् 6a² होगा।
घन के सम्पूर्ण पृष्ठ का क्षेत्रफल = 6 a² वर्ग मात्रक
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल
एक घनाभ का वक्र पृष्ठीय क्षेत्रफल निकालने के लिए हमें समझना होगा की उसका वक्र पृष्ठ क्या होता है। एक घनाभ के वक्र पृष्ठ में ऊपर एवं नीचे के दो आयतों को छोड कर बाकी चारों आयत होते हैं। अतः वक्र पृष्ठ निकालने के लिए हमें ऊपर निचे के आयतों को छोड़ कर बाकी चार आयातों का क्षेत्रफल निकालना होगा।
दिए गए चार आयातों का क्षेत्रफल = 2 × b × h + 2 × h × l
= 2 × h × (l+b)
हल सहित उदाहरण
मैरी अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक घनाभाकार बॉक्स पर रखना चाहती है, जिसे सान्ता क्लॉज के चित्र के साथ एक रंगीन कागज से ढका जाना है। उसका यह जानना आवश्यक है कि उसे कितना कागज खरीदना चाहिए। यदि उपरोक्त बॉक्स की लंबाई, चौड़ाई और ऊँचाई क्रमशः 80 cm, 40 cm और 20 cm हैं, तो उसे 40 cm भुजा वाली कागज की कितनी वर्गाकार शीटों की आवश्यकता होगी?
हलः
चूँकि मैरी बॉक्स के ऊपरी पृष्ठ को कागज से ढकना चाहती है, इसलिए इस कार्य के लिए आवश्यक कागज इस बॉक्स के पृष्ठीय क्षेत्रफल के बराबर होगा, जो एक घनाभ के आकार का है।
बॉक्स की लंबाई 80 cm, चौड़ाई 40 cm और ऊँचाई 20 cm है।
अतः, बॉक्स का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2[(80 × 40) + (40 × 20) + (20 × 80)] cm²
= 2[3200 + 800 + 1600] cm²
= 2 × 5600 cm² = 11200 cm²
अब, प्रत्येक शीट का क्षेत्रफल = 40 × 40 cm² = 1600 cm²
अतः, वांछित शीटों की संख्या = बक्स का पृष्ठीय क्षेत्रफल/ एक शीट का क्षेत्रफल
= ![]() = 7
= 7
इसलिए मैरी को कागज की 7 शीटों की आवश्यकता है।
एक लंब वृत्तीय शंकु का पृष्ठीय क्षेत्रफल
शंकु एक त्रिविमीय संरचना होती हैं जो शीर्ष बिंदु और एक आधार को मिलाने वाली रेखाओं द्वारा निर्मित होती हैं यदि किसी शंकु का आधार एक वृत्त हो तो वह लम्ब वृतीय शंकु कहलाता हैं।
शंकु का वक्र पृष्ठीय क्षेत्रफल= ![]() × आधार की परिधि × तिर्यक ऊँचाई ==
× आधार की परिधि × तिर्यक ऊँचाई == ![]() × l × 2πr
× l × 2πr
= πrl
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल = वक्रप्रष्ठ + आधार का क्षेत्रफल = πr (l + r)
शंकु की तिर्यक ऊँचाई = √(त्रिज्या)² + (ऊँचाई)²
l = √(r² + h²)
जहाँ r आधार की त्रिज्या है और l तिर्यक ऊँचाई तथा h शंकु की ऊँचाई है।
उदाहरण हल सहित
एक लंब वृत्तीय शंकु का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए, जिसकी तिर्यक ऊँचाई 10 cm है और आधार की त्रिज्या 7 cm है।
हल:
वक्र पृष्ठीय क्षेत्रफल = πrl
= ![]() × 7 × 10 cm²
× 7 × 10 cm²
= 220 cm²
गोले का पृष्ठीय क्षेत्रफल
गोला एक त्रिविमीय आकृति (ठोस आकृति) है, जो आकाश में स्थित उन सभी बिंदुओं से मिल कर बनी है जो एक निश्चित बिंदु से (जो गोले का केन्द्र कहलाता है) से एक अचर या निश्चित दूरी पर होते हैं (जो गोले की त्रिज्या कहलाती है)। गोले का केवल एक पृष्ठ होता है।
त्रिज्या r वाले एक गोले का पृष्ठीय क्षेत्रफल = त्रिज्या r वाले चार वृत्तों का क्षेत्रफल
= 4πr²
अर्धगोले का क्षेत्रफल
यदि एक ठोस गोले को इसके केंद्र से जाते हुए एक तल द्वारा दो भागों में काट लें। तो प्रत्येक आधा भाग अर्धगोला कहलाता है।
अर्धगोला का पृष्ठीय क्षेत्रफल
अर्धगोले में दो पृष्ठ होते हैं इनमें एक वक्रीय है और एक समतल फलक है (आधार)।
अर्धगोले का वक्र पृष्ठीय क्षेत्रफल गोले के पृष्ठीय क्षेत्रफल का आधा, अर्थात् ![]() × 4πr² है।
× 4πr² है।
= 2πr²
अतः अर्धगोले का वक्र पृष्ठीय क्षेत्रफल = = 2πr²
जहाँ r उस गोले की त्रिज्या है जिसका अर्धगोला एक भाग है।
अब दोनों फलकों को लेने पर, इसका कुल पृष्ठीय क्षेत्रफल = 2πr² + πr² है।
अतः, अर्धगोले का कुल पृष्ठीय क्षेत्रफल = 3πr²
हल सहित उदाहरण
7 cm त्रिज्या वाले एक गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
7 cm त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल = 4πr² = 4 × ![]() × 7 × 7 cm² = 616 cm²
× 7 × 7 cm² = 616 cm²
घनाभ का आयतन
घनाभ के आयतन से तात्पर्य है कि घनाभ द्वारा कुल घेरा गया स्थान (लम्बाई, चौड़ाई तथा ऊंचाई), अगर हम उसमें कोई चीज़ भरें तो उसमें उस चीज़ की कितनी मात्र आ जायेगी। जैसे अगर हम इस घनाभ में पानी भरना चाहें तो कितनी मात्र में पानी इस घनाभ के अन्दर आ जाएगा। इसका मात्रक गहन इकाई होता है।
एक घनाभ का आयतन निम्न सूत्र से निकाल सकते हैं। हमें उस घनाभ की लम्बाई, चौड़ाई एवं ऊंचाई ज्ञात होनी चाहिए।
घनाभ का आयतन = लम्बाई × चौड़ाई × ऊंचाई
या = l × b × h घन इकाई
यहाँ l = लम्बाई, b = चौड़ाई तथा h = ऊँचाई है।
नोट:
यदि वस्तु खोखली है, तो उसका अभ्यंतर रिक्त होता है, जिसे हवा या द्रव से भरा जा सकता है। यह द्रव उस वस्तु (बर्तन) के आकार का हो जाता है। इस स्थिति में, बर्तन के अभ्यंतर में (अंदर) जितनी वस्तु (या द्रव) भरा जाता है वह उसकी धारिता कहलाती है।
घन का आयतन
घन एक विशेष प्रकार का घनाभ होता है जिसके सभी पृष्ठ वर्गाकार और बराबर होते हैं अर्थात् इसकी लम्बाई, चौड़ाई और ऊंचाई समान होती है। माना घन की एक भुजा a है। इस प्रकार घन का आयतन होगा
a × a x a = a³ घन इकाई
बेलन का आयतन
बेलन एक त्रिआयामी आकृति है बेलन का आयतन इसके द्वारा घेरा गया स्थान है बेलन का आधार वृताकार होता है।
अतः बेलन का आयतन = आधार का क्षेत्रफल × उंचाई
= πr² × h
यहाँ r वृताकार आधार की त्रिज्या है तथा h बेलन की ऊँचाई है।
उदाहरण:
किसी मंदिर के खंभे बेलनाकार हैं। यदि प्रत्येक खंभे का आधार 20 cm त्रिज्या का एक वृत्तीय क्षेत्र है और ऊँचाई 10 m है, तो ऐसे 14 खंभे बनाने में कितने कंक्रीट मिश्रण की आवश्यकता होगी?
हल:
चूँकि कंक्रीट मिश्रण जिससे खंभा बनाया जाएगा उस पूरे खंभे के स्थान को भर देगा, इसलिए हमें बेलनों के आयतनों को ज्ञात करने की आवश्यकता है।
बेलन के आधार की त्रिज्या = 20 cm
बेलनाकार खंभे की ऊँचाई = 10 m = 1000 cm
इसलिए, एक खंभे का आयतन = πr²h
= ![]() × 20 × 20 × 1000 cm³
× 20 × 20 × 1000 cm³
= ![]() cm³
cm³
= ![]() m³ (1000000 cm³ = 1m³)
m³ (1000000 cm³ = 1m³)
अतः, 14 खम्भों का आयतन = ![]() × 14 m³
× 14 m³
= 17.6 m³
इसलिए, 14 खंभों के लिए 17.6 m³ कंक्रीट मिश्रण की आवश्यकता होगी।
लम्ब वृत्तीय शंकु का आयतन
एक लम्ब वृतीय शंकु जिसके आधार की त्रिज्या r है तथा उंचाई h है का आयतन निम्नलिखित सूत्र से ज्ञात कर सकते हैं:
शंकु का आयतन = ![]() × π × r² × h
× π × r² × h
हम निष्कर्ष निकाल सकते हैं कि तीन शंकुओं का आयतन बेलन के आयतन के बराबर है। इसका अर्थ है कि यदि शंकु और बेलन की आधार त्रिज्या एक ही हो और ऊँचाई भी एक ही हो, तो शंकु का आयतन बेलन के आयतन का एक-तिहाई होता है।
शंकु का आयतन = ![]() πr²h
πr²h
उदाहरण
किसी शंकु की ऊँचाई और तिर्यक ऊँचाई क्रमशः 21 Cm और 28 Cm हैं। इसका आयतन ज्ञात कीजिए।
l² = r² + h² से हमें प्राप्त होता है:
r = √(l² – h²) cm
= √(28² – 21²) cm = 7√7 cm
अतः, शंकु का आयतन = ![]() πr²h
πr²h
= ![]() cm³
cm³
= 7546 cm³
गोले का आयतन
सामान्यतः गोले के आयतन को दो प्रकार से परिभाषित कर सकते है। ठोस गोला तथा खोखला गोला। इन दोनों गोला का आयतन एक दूसरें से भिन्न होता है। महान गणितज्ञ ग्रीक दार्शनिक आर्किमिडीज ने गोले के आयतन का सूत्र खोजा था. आर्किमिडीज के अनुसार इसे निम्न प्रकार ज्ञात कर सकते है।
गोले का आयतन उसे परिबद्ध करने वाले बेलन के आयतन का दो-तिहाई होता है, जो ऐसा सबसे छोटा बेलन हो जिसमें गोले को रखा जा सकता हो।
अर्थात, एक गोलाकार वस्तु को एक खोखले बेलन के अंदर रखा जाता है, जहाँ गोलाकार वस्तु की त्रिज्या बेलन के वृत्ताकार आधारों की त्रिज्या के बराबर होती है। और गोले का व्यास बेलन की ऊंचाई के बराबर होता है।
गोले का आयतन= बेलन के आयतन का ![]() भाग
भाग
बेलन का आयतन = πr²h
इसलिए गोले का आयतन = ![]() (πr²h)
(πr²h)
जहाँ r त्रिज्या और h बेलन की ऊंचाई है
हम जानते हैं कि बेलन की ऊंचाई h = गोले का व्यास (2r) (व्यास= 2 × त्रिज्या)
अतः गोले का आयतन = ![]() (πr² × 2r)
(πr² × 2r)
या = ![]() πr³
πr³
इस प्रकार गोले का आयतन = ![]() (πr³)
(πr³)
11.2 Cm त्रिज्या वाले गोले का आयतन ज्ञात कीजिए।
गोले का वाँछित आयतन = ![]() πr³
πr³
= ![]() ×
× ![]() × 11.2 × 11.2 × 11.2 cm³
× 11.2 × 11.2 × 11.2 cm³
= 5887.32 cm³
उदाहरण
एक शॉट-पट्ट 4.9 cm त्रिज्या वाला एक धातु का गोला है। यदि इस धातु का घनत्व 7.8 ग्राम प्रति cm³ है, तो शॉट-पट्ट का द्रव्यमान ज्ञात कीजिए।
हल:
चूँकि शॉट-पट्ट धातु का एक ठोस गोला है तथा द्रव्यमान आयतन और घनत्व के गुणनफल के बराबर होता है, इसलिए पहले हमें शॉट-पट्ट का आयतन ज्ञात करना चाहिए।
गोले का आयतन = ![]() (πr³)
(πr³)
= ![]() ×
× ![]() × 4.9 × 4.9 × 4.9 cm³
× 4.9 × 4.9 × 4.9 cm³
= 493 cm³
साथ ही, 1 cm³ धातु का द्रव्यमान = 7.8 ग्राम
अतः, शॉट-पट्ट का द्रव्यमान = 7.8 × 493 ग्राम
= 3845.44 ग्राम = 3.85 किलोग्राम (लगभग)
खोखले गोले का आयतन
खोखले गोले का आयतन ठोस गोले से भिन्न होता है। इसकी दो त्रिज्याएँ होती हैं एक बाह्य और दूसरी आंतरिक। अतः खोखले गोले का आयतन
निम्न प्रकार से ज्ञात कर सकते हैं:
खोखले गोले का आयतन = ![]() π(R³ – r³)
π(R³ – r³)
जहाँ R गोले की बाहरी त्रिज्या है तथा r आंतरिक त्रिज्या है।
अर्द्ध गोले का आयतन
अर्द्ध गोले का आयतन पूर्ण गोले आधा होता है। जिसको निम्न प्रकार से ज्ञात कर सकते हैं:
अर्द्ध गोले का आयतन = ![]() गोले का आयतन
गोले का आयतन
= ![]() (
(![]() πr³)
πr³)
अर्थात् ![]() πr³
πr³
जहाँ r अर्धगोले की त्रिज्या है।
उदाहरण
एक गोले के व्यास में 25% की कमी हो जाती है। उसका वक्र पृष्ठीय क्षेत्रफल कितने प्रतिशत कम हो गया है?
माना गोले का व्यास d है।
अतः त्रिज्या r₁ = ![]()
प्रश्नानुसार गोले के व्यास में 25% की कमी हो जाती है।
इस प्रकार नई त्रिज्या r₂ =![]() –
– ![]() ×
× ![]() =
= ![]() d
d
गोले का वक्र पृष्ठीय क्षेत्रफल (त्रिज्या r₁ के साथ) S₁ = 4 π r₁²
= 4 × π × (![]() )²
)²
= π d²
गोले का वक्र पृष्ठीय क्षेत्रफल (त्रिज्या r₂ के साथ) S₂ = 4 × π × (![]() )²
)²
= ![]() π d²
π d²
गोले के पृष्ठीय क्षेत्रफल में कमी = π d² – ![]() π d²
π d²
= ![]() π d²
π d²
गोले के पृष्ठीय क्षेत्रफल में प्रतिशत में कमी = 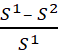 × 100
× 100
= 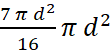 × 100 =
× 100 = ![]()
= 43.75%
We hope that class 9 Math Chapter 13 पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes) Notes in Hindi helped you. If you have any queries about class 9 Math Chapter 13 पृष्ठीय क्षेत्रफल और आयतन (Surface Areas and Volumes) Notes in Hindi or about any other Notes of class 9 Math in Hindi, so you can comment below. We will reach you as soon as possible…