पाठ – 5
केंद्रीय प्रवृत्ति की माप
In this post we have given the detailed notes of class 11 Economics chapter 5 केंद्रीय प्रवृत्ति की माप (Measures of Central Tendency) in Hindi. These notes are useful for the students who are going to appear in class 11 board exams.
इस पोस्ट में कक्षा 11 के अर्थशास्त्र के पाठ 5 केंद्रीय प्रवृत्ति की माप (Measures of Central Tendency) के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 11 में है एवं अर्थशास्त्र विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board |
| Textbook | NCERT |
| Class | Class 11 |
| Subject | Economics |
| Chapter no. | Chapter 5 |
| Chapter Name | केंद्रीय प्रवृत्ति की माप (Measures of Central Tendency) |
| Category | Class 11 Economics Notes in Hindi |
| Medium | Hindi |
Chapter – 5 केंद्रीय प्रवृत्ति की माप
औसत एवं समांतर माध्य
- केन्द्रीय प्रवृति के मापक:
- किसी सांख्यिकी श्रृंखला का वह मूल्य जो केन्द्रीय मूल्य का प्रतिनिधित्व करता हो केन्द्रीय प्रवृति का मापक कहलाता है|
केन्द्रीय प्रवृति के मापक तीन प्रकार के होते हैं|
- माध्य (Mean):
- माध्यक या मध्यिका (Median):
- बहुलक (Mode):
केन्द्रीय प्रवृति के मापक सारी श्रेणी का प्रतिनिधित्व करती है|
सांख्यिकीय औसत
सांख्यिकीय औसत वह मूल्य होता है सभी मदों का केन्द्रिय मूल्य होता है और यह सबका प्रतिनिधित्व करता है|
औसत का कार्य:
- औसत किसी जटिल और अव्यवस्थित आँकड़ों का सरल तथा संक्षिप्त विवरण प्रस्तुत करता है|
- इससे आँकड़ों को समझना आसान हो जाता है|
- औसत की सहायता से दो या दो से अधिक समूहों की तुलना आसान हो जाता है|
- यह आर्थिक नीतियों के निर्धारण में सहायक होता है|
- सांख्यिकीय विश्लेषण काफी हद तक औसत के अनुमान पर आधारित होते हैं जिसके आधार पर यह अनुमान लगाया जा सकता है कि कितने आँकड़े औसत से अधिक है और कितने औसत से कम हैं|
- औसत केन्द्रिय मूल्य होता है जो सभी आँकड़ों का प्रतिनिधित्व करता है|
सांख्यिकीय औसत के प्रकार :
इसे दो भागों में बाँटा गया है|
गणितीय औसत
- समांतर माध्य
- गुणोत्तर माध्य
- हरात्मक माध्य
स्थिति संबंधित औसत
- मध्यिका
- विभाजन मूल्य
- भूयिष्ठक या बहुलक
समांतर माध्य :
- समांतर माध्य किसी श्रृंखला के सभी मदों का एक औसत होता है| यह केन्द्रीय प्रवृति का सबसे सरलतम मापक होता है|
- समान्तर माध्य = मदों का कुल योग/मदों की कुल संख्या
- समांतर माध्य वह संख्या है जो किसी श्रृंखला के सभी मदों के योग में उनकी संख्या से भाग देने पर प्राप्त होता है|
समांतर माध्य के दो प्रकार होते हैं:
- सरल समांतर माध्य: वह माध्य जिसमें किसी श्रृंखला के सभी मदों समान महत्व दिया जाता है उसे सरल समांतर माध्य कहते हैं|
- भारित समांतर माध्य: वह माध्य जिसमें किसी श्रृंखला के विभिन्न मदों को उनके तुलनात्मक महत्त्व के अनुसार भार (weight) दिया जाता है भारित माध्य कहलाता है|
श्रृंखलाओं के आधार पर समांतर माध्य ज्ञात करने की विधि:
व्यक्तिगत श्रृंखला का समांतर माध्य:
2, 5, 3, 7, 8, 1, 6, 9, 5, 10, 6
समांतर माध्य ज्ञात करने की विधि:
प्रत्यक्ष विधि (Direct Method):
सूत्र:
![]()
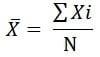
उदाहरण:- 2, 5, 3, 7, 8, 1, 6, 9, 5, 10, 6
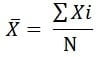
हल:
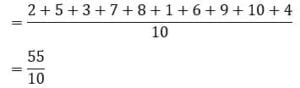
= 5.5
लघु-विधि (Short-cut Method):
- लघु विधि का प्रयोग तब किया जाता है जब मदों की संख्या बड़ी हो| बड़ी संख्या वाले मदों का समांतर माध्य ज्ञात करने के लिए यह एक उपयुक्त विधि है| इसमें गुणा की क्रिया असानी से हो जाता है|
सूत्र:
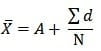
जहाँ Σd = X – A
विचलनों का योग = मद का मूल्य – कल्पित माध्य [A एक कल्पित माध्य है ]
उदाहरण 2:
किसी विद्यालय के ग्यारहवीं कक्षा के 10 विद्यार्थियों का गणित विषय में प्राप्त अंक निम्न लिखित है| लघु विधि द्वारा माध्य ज्ञात कीजिये|
प्राप्त अंक | 35 | 40 | 45 | 50 | 55 | 65 | 70 | 80 | 85 | 90 |
हल:
विद्यार्थियों का क्रम | प्राप्त अंक | d = X – A |
1 2 3 4 5 6 7 8 9 10 | 35 40 45 50 55 65 = (A) माना 70 80 85 90 | 35 – 65 = – 30 40 – 65 = – 25 45 – 65 = – 20 50 – 65 = – 15 55 – 65 = – 10 65 – 65 = 0 70 – 65 = 5 80 – 65 = 15 85 – 65 = 20 90 – 65 = 35 |
N = 10 |
| Σd = – 100 + 75 = – 25 |
यहाँ सभी ऋणात्मक विचलनों का योग = – 100
और सभी धनात्मक विचलनों का योग = 75 है इसलिए Σd = -25
A = 65 और N = 10
लघु-विधि से
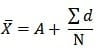
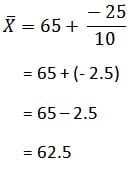
विविक्त या खंडित श्रृंखला का समांतर माध्य:
निम्न सारणी में दिए आँकड़ें विविक्त या खंडित श्रृंखला (Descrete Series) के है| इस प्रकार के आँकड़ों का समांतर माध्य ज्ञात करने के लिए नीचे बताए विधि के अनुसार समांतर माध्य ज्ञात करे|
उदाहरण 3:
50 विद्यार्थियों का विषय अर्थशास्त्र में 100 अंक में से निम्नलिखित अंक प्राप्त हुए है| इनका माध्य ज्ञात कीजिये|
अंक | 30 | 40 | 50 | 60 | 70 | 80 | 90 | कुल |
विद्यार्थियों की संख्या | 6 | 5 | 12 | 7 | 9 | 3 | 8 | 50 |
विविक्त या खंडित श्रृंखला का समांतर माध्य निम्नलिखित विधियों के द्वारा ज्ञात किया जाता है|
(1) प्रत्यक्ष विधि (Direct Method) : यह विधि सीधी और सरल होती है|
X = मद; f = बारंबारता
सूत्र:
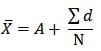
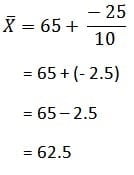
विविक्त या खंडित श्रृंखला का समांतर माध्य:
निम्न सारणी में दिए आँकड़ें विविक्त या खंडित श्रृंखला (Descrete Series) के है| इस प्रकार के आँकड़ों का समांतर माध्य ज्ञात करने के लिए नीचे बताए विधि के अनुसार समांतर माध्य ज्ञात करे|
उदाहरण 3:
50 विद्यार्थियों का विषय अर्थशास्त्र में 100 अंक में से निम्नलिखित अंक प्राप्त हुए है| इनका माध्य ज्ञात कीजिये|
अंक | 30 | 40 | 50 | 60 | 70 | 80 | 90 | कुल |
विद्यार्थियों की संख्या | 6 | 5 | 12 | 7 | 9 | 3 | 8 | 50 |
विविक्त या खंडित श्रृंखला का समांतर माध्य निम्नलिखित विधियों के द्वारा ज्ञात किया जाता है|
(1) प्रत्यक्ष विधि (Direct Method) : यह विधि सीधी और सरल होती है|
X = मद; f = बारंबारता
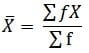
![]()
हल :
उदाहरण 3
अंक (X) | विद्यार्थियों की संख्या (f) | fX |
30 40 50 60 70 80 90 | 6 5 12 7 9 3 8 | 180 200 600 420 630 240 720 |
| Σf = 50 | ΣfX = 2990 |
प्रत्यक्ष विधि से-
ΣfX = 2990, Σf = 50
(2) लघु-विधि (Short-cut Method): यह विधि प्रत्यक्ष विधि से भी सरल है क्योंकि इसमें गुणा
(x) और जमा (+) की क्रिया आसान हो जाता है|
(3) पद विचलन विधि (Step Deviation Method):
आवृति वितरण अथवा अखंडित श्रृंखला का समांतर माध्य:
केन्द्रीय प्रवृति के माप – समांतर माध
भारित समांतर माध्य
वह माध्य जिसमें श्रृंखला के प्रत्येक मद को उसके तुलनात्मक महत्त्व के अनुसार भाग देकर माध्य की गणना की जाती है|
सूत्र (Formula):

समांतर माध्य के गुण:
- समांतर माध्य सभी माध्यों से सरल होता है और इसे एक साधारण व्यक्ति भी असानी से समझ सकता है|
- समांतर माध्य की गणना करना बहुत ही सरल है|
- समांतर माध्य एक निश्चित संख्या होती है इसमें अनुमान का कोई स्थान नहीं होता है|
- समान्तर माध्य श्रृंखला से सभी मूल्यों पर आधारित होता है और सभी मदों का प्रतिनिधित्व करता है|
- समांतर माध्य के आधार पर अन्य श्रृंखलाओं से तुलना आसान होता है|
समांतर माध्य के अवगुण:
- समांतर माध्य का मुख्य दोष यह है कि ये सभी मूल्यों पर आधारित होने के कारण सीमांत मूल्यों का अधिक प्रभाव पड़ता है|
- समांतर माध्य कई बार ऐसी संख्या होती है जो श्रृंखला में होती ही नहीं है|
- समांतर माध्य द्वारा कई बार बहुत ही हास्यप्रद निष्कर्ष निकलते हैं|
- समान्तर माध्य द्वारा निकले गए निष्कर्ष कई बार गलत होते हैं|
We hope that class 11 Statistics for Economics chapter 5 केंद्रीय प्रवृत्ति की माप (Measures of Central Tendency) notes in Hindi helped you. If you have any query about class 11 Statistics for Economics chapter 5 केंद्रीय प्रवृत्ति की माप (Measures of Central Tendency) notes in Hindi or about any other notes of class 11 Statistics for Economics in Hindi, so you can comment below. We will reach you as soon as possible…