पाठ – 6
परिक्षेपण के माप
In this post we have given the detailed notes of class 11 Economics chapter 6 परिक्षेपण के माप (Measures of Dispersion) in Hindi. These notes are useful for the students who are going to appear in class 11 board exams.
इस पोस्ट में कक्षा 11 के अर्थशास्त्र के पाठ 6 परिक्षेपण के माप (Measures of Dispersion) के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 11 में है एवं अर्थशास्त्र विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board |
| Textbook | NCERT |
| Class | Class 11 |
| Subject | Economics |
| Chapter no. | Chapter 6 |
| Chapter Name | परिक्षेपण के माप (Measures of Dispersion) |
| Category | Class 11 Economics Notes in Hindi |
| Medium | Hindi |
Chapter – 6 परिक्षेपण के माप
परिक्षेपण के माप
- परिक्षेपण: परिक्षेपण का शाब्दिक अर्थ विचरणशीलता अथवा बिखराव है, यह किसी श्रृंखला के विभिन्न मदों में आपस में कितना अंतर तथा माध्य से कितना अंतर है यह इस तथ्य को बताता है|
- परिक्षेपण का माप: वह सांख्यिकी विधि जिससे केन्द्रीय प्रवृति के माप के बिखराव के विस्तार को मापा जाता है, परिक्षेपण का माप कहलाता है|
1. निरपेक्ष माप ( Absolute Measure): जब परिक्षेपण के माप को उन्हीं ईकाइयों में व्यक्त किया जाता है जिन ईकाइयों में मूल आँकड़ें दिए गए हैं तो यह निरपेक्ष माप कहलाता है|
- जैसे – इसके द्वारा दो या दो से अधिक श्रृंखलाओं की तुलना नहीं की जा सकती है|
2. सापेक्ष माप (Relative Measure): सापेक्ष माप में आँकड़ों के अंतर या बिखराव (परिक्षेपण के माप ) को अनुपात या प्रतिशत के रूप में व्यक्त किया जाता है, तो यह सापेक्ष माप कहलाता है|
जैसे – 10 प्रतिशत विद्यार्थी अनुपस्थित है|
उपयोग: जहाँ दो या दो से अधिक श्रृंखलाओं की तुलना करनी है|
- इसे परिक्षेपण गुणांक (Coefficient of Dispersion) भी कहा जाता है|
परिक्षेपण ज्ञात करने की विधि
परिक्षेपण के निरपेक्ष माप ज्ञात करने की विधियां निम्न है-
- परास या विस्तार (Range)
- चतुर्थक विचलन (Quartile Deviation)
- अंतर-चतुर्थक विस्तार(Inter-Quartile Range)
- माध्य-विचलन (Mean Deviation)
- मानक या प्रमाप विचलन (Standerd Deviation)
- लॉरेन्ज वक्र (Lorenz Curve)
परिक्षेपण के सापेक्ष माप ज्ञात करने की विधियाँ निम्न है-
- परास या विस्तार गुणांक (Coefficient of Range)
- चतुर्थक विचलन गुणांक (Coefficient of Quartile Deviation)
- माध्य विचलन गुणांक (Coefficient of Mean Deviation)
- मानक या प्रमाप विचलन गुणांक (Coefficient of Standerd Deviation)
परास या विस्तार (Range): किसी श्रृंखला के अधिकतम मूल्य (Highest Value) तथा न्यूनतम मूल्य (Lowest Value) के अंतर को परास या विस्तार (range) कहा जाता है| इसे निम्न सूत्र द्वरा निकाला जाता है|
परास (Range) = H – L
{जहाँ H = मदों की अधिकतम मूल्य (Highest Value) तथा L मदों की न्यूनतम मूल्य (Lowest Value)}
परास या विस्तार गुणांक (Coefficient of Range):
- परास या विस्तार गुणांक किसी श्रेणी के मदों की अधिकतम मूल्य (Highest Value) तथा न्यूनतम मूल्य (Lowest Value) के अंतर तथा इनके योग का अनुपात परास गुणांक (Coefficient of Range) कहलाता है|
- इसकों ज्ञात करने के लिए निम्न सूत्र प्रयोग किये जाते है|
- परास गुणांक (CR) = H – L /H + L
विभिन्न श्रृंखलाओं के लिए परास या विस्तार
1. व्यक्तिगत श्रृंखला (Individual Series) में
- परास (Range) तथा परास गुणांक (CR):
- व्यक्तिगत श्रृंखला में श्रृंखला के मदों (items) की अधिकतम मूल्य (H) तथा उन्ही मदों की न्यूनतम मूल्य (L) का अंतर परास (Range) कहलाता है|
उदाहरण:-
11 वीं कक्षा के कुछ छात्रों का प्रतिदिन का जेब खर्च निम्नलिखित है| इनके जेब खर्च का परास (range) तथा परास गुणांक (CR) ज्ञात कीजिए|
20, 25, 30, 35, 40, 50, 60, 70 , 75, 80, 90, 100
व्यक्तिगत श्रृंखला के इस श्रेणी के मदों का अधिकतम मूल्य (H) = 100 है, तथा न्यूनतम मूल्य (L) = 20 है|
हल:
H = 100
L = 20
इसलिए, परास (R) = H – L
= 100 – 20
= 80
अत: जेब खर्च का परास 80 है|
परास गुणांक (CR) = H – L / H + L
= 100 – 20 / 100 + 20
= 80 / 120
= 0.67
2. विविक्त श्रृंखला या खंडित श्रृंखला (Discrete Series) या आवृति विन्यास श्रृंखला में
इसमें भी मदों की अधिकतम मूल्य (H) तथा न्यूनतम मूल्य (L) के अंतर द्वारा ही परास (Range) ज्ञात किया जाता है| परन्तु इसकी गणना में आवृतियों (Frequency) का कोई लेना-देना नहीं है|
उदाहरण:-
निम्नलिखित आँकड़ों से परास (range) तथा परास गुणांक (Coefficent of range) ज्ञात कीजिए|
अंक (Marks) | 6 | 7 | 8 | 10 | 12 | 14 | 15 |
विद्यार्थियों की संख्या (f) | 12 | 6 | 10 | 8 | 5 | 3 | 6 |
इस प्रश्न को हल करते समय हमें विद्यार्थियों की संख्या (Number of Student) जो की आवृति (frequency) है हल से कोई लेना देना नहीं है| हमें सिर्फ अंक (Marks) के अधिकतम मूल्य (H) तथा न्यूनतम मूल्य (L) को ही लेना है|
हल:
H = 15, L = 6
परास (Range) = H – L
= 15 – 6
= 9
अत: R = 9
परास गुणांक (CR) = H – L / H + L
= 15 – 6 / 15 + 6
= 9 / 21
= 0.428
अत: CR = 0.43 (निकटतम मान रखने पर)
मानक विचलन
- इसे ग्रीक के अक्षर σ द्वरा दर्शाया जाता है|
- मानक विचलन की विशेषताएँ :
इसकी दो विशेषताएँ हैं :
- इसके मूल्य के विचलन हमेशा समांतर माध्य से ही निकाले जाते हैं|
- (+) तथा (-) चिन्हों को छोड़ा नहीं जाता है|
मानक विचलन की गणना :
व्यक्तिगत श्रृंखला में : मानक विचलन
विधियाँ:
1. प्रत्यक्ष विधि (Direct Method): इस विधि का उपयोग तब किया जाता है जब मदें (items) एवं अवृतियाँ एक या दो अंकों की होती है एवं समांतर माध्य पूर्ण अंक में आता है जिसमें गुणन क्रिया आसानी से किया जा सके|
steps:
- सर्वप्रथम निम्न सूत्र द्वारा श्रृंखला का समांतर माध्य ज्ञात किया जाता है|
- इसके बाद प्रत्येक मूल्य में से समांतर माध्य को घटाकर विचलन (deviation) x = X – X निकाला जाता है|
- इन विचलनों (x) का वर्ग (x2) ज्ञात किया जाता है| फिर सबको जोड़ लिया जाता है अर्थात ∑x2 ज्ञात किया जाता है|
2. लघु विधि (Short-CutMethod):
- दिए हुए मदों में से किसी एक मद (items) को कल्पित माध्य (Assumed Mean) अर्थात A मान लिया जाता है| नोट : (वैसे किसी भी मद को कल्पित माध्य A माना जा सकता है लेकिन बीच के कोई मद (items) को यदि A माना जाय तो हल करने में असानी होता है|)
- कल्पित माध्य से एक-एक कर सभी मदों (items) का विचलन (dx = X – A) निकला जाता है|
- उसके बाद सभी विचलनों का योग ∑dx ज्ञात किया जाता है|
- अगले स्तम्भ में विचलनों का वर्ग ज्ञात कर फिर उनका योग ∑dx2 प्राप्त किया जाता है|
- इस विधि से मानक विचलन (σ) ज्ञात करने के लिए निम्न सूत्र का उपयोग किया जाता है|
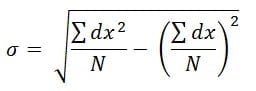
3. पद विचलन विधि (Step deviation Method) :
Steps:
- दिए गए मदों में से किसी एक को कल्पित माध्य (A) मानकर उस कल्पित माध्य से सभी मदों का विचलन (dx = X – A ) निकाला जाता है|
- इन सभी विचलनों को इनके सार्व गुणनखंड द्वारा भाग कर दिया जाता है जिससे पद विचलन (dx’) प्राप्त किया जाता है| इसके लिए सूत्र है dx’ = dx/C,
- फिर इन पद विचलनों का वर्ग (dx’)2 ज्ञात कर लिया जाता है|
- इसके बाद इन विचलनों के वर्गों का योग ∑dx’2 ज्ञात किया जाता है|
- इसके बाद निम्न सूत्र द्वारा मानक विचलन (σ) ज्ञात कर लिया जाता है|
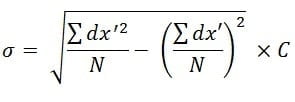
We hope that class 11 Statistics for Economics chapter 6 परिक्षेपण के माप (Measures of Dispersion) notes in Hindi helped you. If you have any query about class 11 Statistics for Economics chapter 6 परिक्षेपण के माप (Measures of Dispersion) notes in Hindi or about any other notes of class 11 Statistics for Economics in Hindi, so you can comment below. We will reach you as soon as possible…