पाठ – 3
दो चर वाले रैखिक समीकरण युग्म
In this post we have given the detailed notes of class 10 Math chapter 3 Pair of Linear Equations in Two Variables in Hindi. These notes are useful for the students who are going to appear in class 10 board exams.
इस पोस्ट में कक्षा 10 के गणित के पाठ 3 दो चर वाले रैखिक समीकरण युग्म के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 10 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Math |
| Chapter no. | Chapter 3 |
| Chapter Name | दो चर वाले रैखिक समीकरण युग्म (Pair of Linear Equations in Two Variables) |
| Category | Class 10 Math Notes in Hindi |
| Medium | Hindi |
पाठ 3 दो चर वाले रैखिक समीकरण युग्म
दो चर वाले रैखिक समीकरण
युग्म समीकरण, जिसको ax + by + c = 0 के रूप में रखा जा सकता है, जहाँ a, b और c वास्तविक संख्याएँ हैं और a और b दोनों शून्य नहीं हैं, दो चरों x और y में एक रैखिक समीकरण कहलाता है। (प्रतिबंध जैसे a और b दोनों शून्य नहीं हैं, हम प्रायः a² + b² ≠ 0 से प्रदर्शित करते हैं।)
दो चरों वाले रैखिक समीकरण ax + by + c = 0 का प्रत्येक हल (x, y) इस समीकरण को निरूपित करने वाली रेखा के एक बिदु के संगत होता है और विलोमतः भी ऐसा होता है।
उदाहरण
समीकरण 2x + 3y = 5 के बाएं पक्ष में x = 1 और y = 1 रखने पर
बायाँ पक्ष 2(1) + 3(1) = 2 + 3 = 5, जो कि दायें पक्ष के बराबर है। अतः x = 1 और y = 1 समीकरण 2x + 3y = 5 का एक हल है।
ज्यामितीय दृष्टिकोण
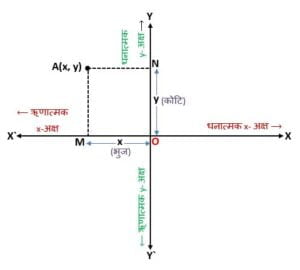
ज्यामितीय दृष्टि से इसका अर्थ है कि बिदु (1, 1) समीकरण 2x + 3y = 5 द्वारा निरूपित रेखा पर स्थित है। इसलिए, समीकरण का प्रत्येक हल उसको निरूपित करने वाली रेखा पर स्थित एक बिदु होता है।
रैखिक समीकरण युग्म
ये दो रैखिक समीकरण उन्हीं दो चरों x और y में हैं। इस प्रकार के समीकरणों को दो चरों में रैखिक समीकरणों का एक युग्म (या रैखिक समीकरण युग्म) कहते हैं।
उदाहरण
- x – 2y = 0 (1)
- 3x + 4y = 20 (2)
हम इन समीकरणों के माध्यम से x और y के मान ज्ञात कर सकते हैं।
ज्यामितीय दृष्टि से रैखिक समीकरण युग्म
एक तल में यदि दो रेखाएँ दी हों, तो निम्न में से केवल एक ही संभावना हो सकती हैः
(i) दोनों रेखाएँ एक बिदु पर प्रतिच्छेद करती हैं।
(ii) दोनों रेखाएँ प्रतिच्छेद नहीं करती हैं, अर्थात् वे समांतर हैं।
(iii) दोनों रेखाएँ संपाती हैं।
स्मरणीय तथ्य
1. दो चरों में दो रैखिक समीकरण एक रैखिक समीकरणों का युग्म कहलाता है। रैखिक समीकरण युग्म का सबसे व्यापक रूप हैः
- a₁ x + b₁ y + c₁ = 0
- a₂ x + b₂ y + c₂ = 0
जहाँ a₁, a₂, b₁, b₂, c₁, c₂ ऐसी वास्विक संख्याएं हैं कि a₁² + b₁² ≠ 0, a₂² + b₂² ≠ 0
2. एक रैखिक समीकरण युग्म को ग्राफीय रूप में निरूपित किया जा सकता है और हल किया जा सकता है।
(i) ग्राफीय विधि द्वारा
(ii) बीजगणितीय विधि द्वारा
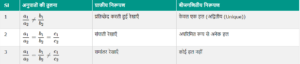
रैखिक समीकरण युग्म के प्रकार (Types Pair of Linear Equations)
- (i) रैखिक समीकरणों का संगत युग्म
- (ii) रैखिक समीकरणों का असंगत युग्म
- (iii) रैखिक समीकरणों का आश्रित युग्म
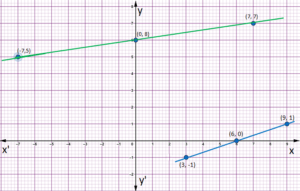
रैखिक समीकरण युग्म का ग्राफीय विधि से हल
एक रैखिक समीकरण युग्म को कैसे ग्राफीय रूप में दो रेखाओं में व्यक्त किया जाता है। आपने यह भी देखा है कि ये रेखाएँ प्रतिच्छेद कर सकती हैं या समांतर हो सकती हैं या संपाती हो सकती हैं। इस स्थिति को निरूपित करने वाले समीकरण ज्यामितीय रूप से बिंदु (4, 2) पर प्रतिच्छेद करने वाली दो रेखाओं को निरूपित करते हैं। इसलिए, बिंदु (4, 2) दोनों समीकरणों x – 2y = 0 और 3x + 4y = 20 को निरूपित करने वाली रेखाओं पर स्थित है और केवल यही उभयनिष्ठ बिंदु है।
रैखिक समीकरण युग्म का बीजगणितीय विधि से सत्यापन
हम बीजगणितीय रूप से यह सत्यापित करेंगे कि x = 4, y = 2 दिए हुए समीकरण युग्म का एक हल है। प्रत्येक समीकरण में x और y के मान रखने पर,
हम प्राप्त करते हैं 4 – 2 × 2 = 0 और 3 × 4 + 4 × 2 = 20 है।
अतः, हमने सत्यापित किया है कि x = 4, y = 2 दोनों समीकरणों का एक हल है।
चूँकि (4, 2) दोनों रेखाओं का केवल एक उभयनिष्ठ बिंदु है, इसलिए दो चरों में रैखिक समीकरण युग्म का एक और केवल एक हल है।
रैखिक समीकरणों का असंगत युग्म
- एक रैखिक समीकरण युग्म, जिसका कोई हल नहीं होता, रैखिक समीकरणों का असंगत युग्म कहलाता है।
रैखिक समीकरणों का संगत युग्म
- एक रैखिक समीकरण युग्म, जिसका हल होता है, रैखिक समीकरणों का संगत युग्म कहलाता है।
दो चरों के रैखिक समीकरणों का आश्रित युग्म
तुल्य रैखिक समीकरणों के एक युग्म के अपरिमित रूप से अनेक हल होते हैं। इस युग्म को दो चरों के रैखिक समीकरणों का आश्रित युग्म कहते हैं। ध्यान दीजिए कि रैखिक समीकरणों का आश्रित युग्म सदैव संगत होता है।
अब हम दो चरों में एक रैखिक समीकरण युग्म द्वारा निरूपित रेखाओं के व्यवहार को तथा हल के अस्तित्व होने को निम्न प्रकार से एक सारांश के रूप में व्यक्त कर सकते हैंः
- (i) रेखाएँ एक बिंदु पर प्रतिच्छेद कर सकती हैं। इस स्थिति में, समीकरण युग्म का अद्वितीय हल होता है (अविरोधी समीकरण युग्म)।
- (ii) रेखाएँ समांतर हो सकती हैं। इस स्थिति में, समीकरणों का कोई हल नहीं होता है (असंगत समीकरण युग्म)।
- (iii) रेखाएँ संपाती हो सकती हैं। इस स्थिति में, समीकरणों के अपरिमित रूप से अनेक हल होते हैं [आश्रित (संगत) समीकरण युग्म]
रैखिक समीकरण युग्म के ज्यामितीय रूप
उदाहरण के लिए नीचे दिए गए रैखिक समीकरण युग्म के गुणांको के सम्बंध से युग्म रेखाओं के निम्नलिखित ज्यामितीय रूप का निरूपण निम्न प्रकार से हैः
- a1 x + b1 y + c1 = 0 ……… (1)
- a2 x + b2 y + c2 = 0 ……… (2)

एक रैखिक समीकरण युग्म को हल करने की बीजगणितीय विधि
एक रैखिक समीकरण युग्म को हल करने के लिए कई बीजगणितीय (बीजीय) विधियाँ हैं। जो निम्न प्रकार से हैं:
प्रतिस्थापन विधि
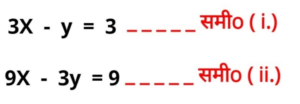
प्रतिस्थापन विधि को कुछ उदाहरण लेकर समझाएँगे।
उदाहरण
प्रतिस्थापना विधि द्वारा निम्न रैखिक समीकरण युग्म को हल कीजिए:
- 7x – 15y = 2 (1)
- x + 2y = 3 (2)
हल:
चरण 1: हम किसी एक समीकरण को लेते हैं और किसी एक चर को दूसरे के पदों में लिखते हैं। आइए समीकरण (2) को लेते हैं:
x + 2y = 3
इस समीकरण को x = 3 – 2y के रूप में लिख सकते हैं।
x = 3 – 2y (3)
चरण 1: अब x का मान समीकरण (1) में प्रतिस्थापित करते हैं। इससे हम पाते हैं:
7(3 – 2y) – 15y = 2
अर्थात 201 – 14y – 15y = 2
अर्थात् – 29y = –19
इसलिए ![]()
चरण 1: अब y का मान समीकरण (3) में प्रतिस्थापित करते हैं। इससे हम पाते हैं:
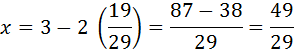
अतः x = 49/29, y = 19/29 दिए गए रैखिक समीकरण युग्म का प्रतिस्थापना विधि द्वारा बीजगणितीय हल है।
उत्तर के सत्यापन्न के लिए x और y के मान को अलग-अलग समीकरण 1 और 2 में रखकर जांच कर सकते हैं।
प्रतिस्थापन विधि क्या है?
हमने एक चर का मान दूसरे चर के पद में व्यक्त करके, रैखिक समीकरण युग्म को हल करने के लिए प्रतिस्थापित किया है। इसलिए इस विधि को प्रतिस्थापन विधि कहते हैं।
विलोपन विधि
रैखिक युग्म समीकरण को बीजगणितीय विधि से हल करने के लिए प्रतिस्थापन विधि के अतिरिक्त अन्य विधि विलोपन की है। जिसमें एक चर को विलुप्त करके एक चर में रैखिक समीकरण प्राप्त करते हैं इससे एक चर का मान निकाल आता है। उसकी सहायता से दुसरे चर का मान भी प्राप्त कर सकते हैं।
इसे एक उदाहरण के माध्यम से समझाते हैं:
उदाहरण
दो व्यक्तियों की आय का अनुपात 9 : 7 है और उनके खर्चों का अनुपात 4 : 3 है। यदि प्रत्येक व्यक्ति प्रति महीने में 2000 रु बचा लेता है, तो उनकी मासिक आय ज्ञात कीजिए।
हल
आइए दोनों व्यक्तियों की मासिक आय को क्रमशः 9x रु तथा 7x रु से निरूपित करें और उनके खर्चों को क्रमशः 4y रु और 3y रु से निरूपित करें। तब, उस स्थिति में बने समीकरण हैंः
9x – 4y = 2000 (1)
और 7x – 3y = 2000 (2)
चरण 1:
y के गुणकों को समान करने के लिए समीकरण (1) को 3 से तथा समीकरण (2) को 4 से गुणा कीजिए। तब हम निम्नलिखित समीकरण प्राप्त करते हैंः
27x – 12y = 6000 (3)
28x – 12y = 8000 (4)
चरण 2:
y को विलुप्त करने के लिए समीकरण (3) को समीकरण (4) में से घटाइए, क्योंकि y के गुणांक समान हैं, इसलिए हम पाते हैंः
(28x – 12y) – (27x – 12y) = 8000 – 6000
अर्थात् x = 2000
चरण 3:
x का मान (1) में प्रतिस्थापित करने पर, हम पाते हैंः
9(2000) – 4y = 2000
अर्थात y = 4000
अतः समीकरणों के युग्म का हल x = 2000, y = 4000 है। इसलिए, व्यक्तियों की मासिक आय क्रमशः रु 18000 तथा रु 14000 हैं।
सत्यापन:
उनकी आय का अनुपात 18000 : 14000 = 9 : 7 है। साथ ही, उनके खर्च का अनुपात
18000 – 2000 : 14000 – 2000 = 16000 : 12000 = 4 : 3 है।
वज्र-गुणन विधि
वज्र गुणन विधि सूत्र (Cross multiplication method formula,formula of cross multiplication method)-
माना दिए गए समीकरण हैं:
![]()
![]()
समीकरण (1) को b2 से तथा समीकरण (2) को b1 से गुणा करने पर-
![]()
![]()
समीकरण (3) में से (4) घटाने पर-
![]()
![]()
इसी प्रकार समीकरण (1) को a2 से तथा समीकरण (2) को b1 से गुणा करने पर-
a1a2x + a2b1y + c1a2 = 0………..(6)
a1a2x + a1b2y + c2a1 = 0………..(7)
समीकरण (6) में से समीकरण (7) को घटाने पर-
(a2b1−a1b2)y = c2a1−c1a2
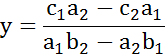
समीकरण (5) से ![]()
उपर्युक्त समीकरणों को निम्न प्रकार लिखा जा सकता है-
![]()
इस परिणाम को निम्न रचना के माध्यम से दर्शा सकते हैं जिससे समीकरणों के हल को सुगमता से स्मरण रख सके।
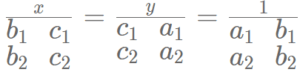
रचना में तीर के निशान का अर्थ दो संख्याओं के गुणा को दर्शाना है।पहले नीचे की ओर गुणा करना है फिर इसमें से ऊपर की ओर गुणा कर गुणनफल घटाना है।
वज्र गुणा के कारण यह वज्र गुणन विधि कहलाती है।इस विधि का प्रयोग से पूर्व समीकरणों के सभी पदों को पहले वाम पक्ष में लेकर दक्षिण पक्ष को शून्य बना देते हैं।प्रथम समीकरण एवं द्वितीय समीकरण में प्रथम चर के गुणांक द्वितीय चर के गुणांक तथा स्वतन्त्र चर से प्रदर्शित करते हैं।
साधनीयता के लिए प्रतिबन्ध (Condition for Solvability)
यदि समीकरण निकाय a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 a1x + b1y + c1 = 0, a2 x + b2y + c2 = 0 हो तो संगत चरों के गुणांकों का अनुपात देखने पर निम्न स्थिति के अनुसार निर्णय किया जाता है।

गुणन विधि के उदाहरण
निम्नलिखित समीकरणों के बारे में जांच कीजिए कि समीकरण निकाय के अद्वितीय हल है, कोई हल नहीं है या अपरिमित हल हैं।यदि किसी निकाय के अद्वितीय हल हैं तो उन्हें ज्ञात कीजिए।
Example-1
2x + y = 35, 3x + 4y = 65
Solution: 2x + y = 35
3x + 4y = 65
समीकरण के सभी पदो को वाम पक्ष में लेने पर-
2x + y – 35 = 0
3x + 4y -65=0

Example-2
2x – y = 6
x – y = 2
Solution: 2x – y = 6
x – y = 2
समीकरण के सभी पदों को वाम पक्ष में लेने पर-
2x – y – 6 = 0
x – y – 2 = 0
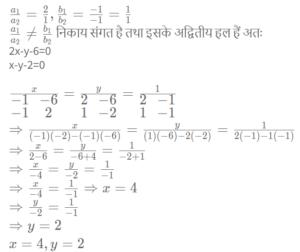

Example-4. k का मान ज्ञात कीजिए यदि समीकरण निकाय का कोई हल नहीं है।
2x + ky = 1
3x – 5y = 7
Solution: 2x + ky = 1
3x – 5y = 7
समीकरण के सभी पदों को वाम पक्ष में लेने पर-
2x + ky – 1 = 0
3x – 5y – 7 = 0
समीकरण निकाय का कोई हल नहीं है अतः
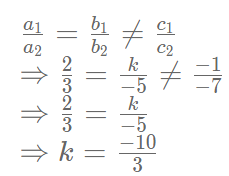

वज्र गुणन विधि की समस्याएं
निम्नलिखित समीकरणों के बारे में जांच कीजिए कि समीकरण निकाय के अद्वितीय हल है, कोई हल नहीं है या अपरिमित हल हैं।यदि किसी निकाय के अद्वितीय हल हैं तो उन्हें ज्ञात कीजिए।
(1.)x+2y+1=0,2x-3y-12=0
(2.)2x+3y-17=0,3x-2y-6=0
k का मान ज्ञात कीजिए यदि समीकरण निकाय का कोई हल नहीं है-
(3.)kx+2y=5,3x+y=1
का वह मान ज्ञात कीजिए जिसके लिए निकाय के
(i) अद्वितीय हल (ii) कोई हल नहीं है।
(4.) 3x + λy – 1 = 0, 2x + y – 9 = 0

उदाहरण
बैंगलोर के एक बस स्टैंड से यदि हम दो टिकट मल्लेश्वरम के तथा 3 टिकट यशवंतपुर के खरीदें, तो कुल लागत रू 46 है। परंतु यदि हम 3 टिकट मल्लेश्वरम के और 5 टिकट यशवंतपुर के खरीदें, तो कुल लागत रू 74 है। बस स्टैंड से मल्लेश्वरम का किराया तथा बस स्टैंड यशवंतपुर का किराया ज्ञात कीजिए।
उदाहरण का हल:
माना बैंगलोर के बस स्टैंड से, मल्लेश्वरम का किराया रू x तथा यशवंतपुर का किराया रू y है। दी गई सूचनाओं से, हम पाते हैंः
2x + 3y = 46, अर्थात् 2x + 3y – 46 = 0 …….. (1)
3x + 5y = 74, अर्थात् 3x + 5y – 74 = 0 ……… (2)
यहाँ पर a₁ = 2, b₁ = 3, c₁ =- 46, a₂ = 3, b₂ = 5, c₂ = -74
वज्र-गुणन विधि से इन समीकरणों को हल करने के लिए, हम निम्न प्रकार से लिख सकते हैंः
x/{ (3) (-74) – (5) (-46)} = y/{(-46)(3) – (-74)(2)} = 1/{(2)(5) – (3)(3)}
- अर्थात् x/(-222 + 230) = y/(-138 + 148) = 1/(10 – 9)
- अर्थात् x/8 = y/10 = 1/1
- अर्थात् x/8 = 1/1
- अर्थात् y/10 = 1/1
- अर्थात् x = 8 और y = 10
अतः, बैंगलोर के बस स्टैंड से, मल्लेश्वरम का किराया रू 8 तथा यशवंतपुर का किराया रू 10 है।
नोट:
अपने उत्तर के सत्यापन्न के लिए हम x और y का मान समीकरण (1) और (2) में रखकर कर सकते हैं।
दो चरों के रैखिक समीकरणों के युग्म में बदले जा सकने वाले समीकरण
हम ऐसे समीकरणों के युग्मों के बारे में चर्चा करेंगे जो रैखिक नहीं है, परंतु कुछ उपयुक्त प्रतिस्थापनों द्वारा इन्हें रैखिक समीकरणों के रूप में बदला जा सकता है।
उदाहरण
समीकरणों के निम्न युग्म को हल कीजिए:
- 2/x + 3/y = 13
- 5/x – 4/y = -2
उदाहरण का हल:
दिए गए समीकरणों के युग्म को इस प्रकार से लिखते हैं:
- 2(1/x) + 3(1/y) = 13 (1)
- 5(1/x) – 4(1/y) = -2 (2)
ये समीकरण ax + by + c= 0 के रूप में नहीं हैं। परंतु, यदि हम समीकरण (1) और (2) में, 1/x = p आयर 1/y = q प्रतिस्थापित करें, तो हम पाते हैंः
- 2p + 3q = 13 (3)
- 5p – 4q = -2 (4)
अतः, समीकरणों को रैखिक समीकरणों के युग्म के रूप में व्यक्त कर दिया है। अब इन्हें किसी भी विधि से हल करके p = 2, q = 3 प्राप्त कर सकते हैं।
यहाँ p = 1/x और q = 1/y है
इसलिए, 1/x = 2 और 1/y = 3
अर्थात् x = ½ और y = 1/3
सत्यापन:
दोनों समीकरणों में x = ½ तथा y = 1/3 रखने पर, हम पाते हैं कि दोनों समीकरण संतुष्ट हो जाते हैं।
इसे एक और व्यवहारिक उदाहरण से समझने कि कोशिश करते हैं:
उदाहरण
एक नाव 10 घंटे में धारा के प्रतिकूल 30 km तथा धारा के अनुकूल 44 km जाती है। 13 घंटे में वह 40 km धारा के प्रतिकूल एवं 55 km धारा के अनुकूल जाती है। धारा की चाल तथा नाव की स्थिर पानी में चाल ज्ञात कीजिए।
उदाहरण का हल
माना नाव की स्थिर जल में चाल x km/h है तथा धारा की चाल y km/h है। साथ ही, नाव की धारा के अनुकूल चाल = (x + y) km/h तथा नाव की धारा के प्रतिकूल चाल = (x – y) km/h होगी।
साथ ही, समय = दूरी/चाल
प्रथम स्थिति में, जब नाव 30 km धारा के प्रतिकूल चलती है, माना घंटों में लिया गया समय
ज1 है। तबचाल
प्रथम स्थिति में, जब नाव 30 शउ धारा के प्रतिकूल चलती है, माना घंटों में लिया गया समय t₁ है। तब
t₁ = 30/(x – y)
माना t₂ घंटों में वह समय है जिसमें नाव 44 km धारा के अनुकूल चलती है। तब, t₂ = 44/(x + y) है। कुल लगा समय t₁ + t₂, 10 घंटा है। अतः, हमें समीकरण मिलता हैः
- 30/(x – y) + 44/(x + y) = 10 (1)
दूसरी स्थिति में, 13 घंटों में वह 40 km धारा के प्रतिकूल और 55 km धारा के अनुकूल चलती है। हम इससे समीकरण प्राप्त करते हैं:
- 40/(x – y) + 55/(x + y) = 13 (2)
उपरोक्त समीकरणों को रैखिक समीकरणों के युग्म के रूप में व्यक्त करने के लिए
- 1/(x – y) = u और 1/(x + y) = v (3)
- 30u + 44v = 10 या 30u + 44v – 10 = 0 (4)
- 40u + 55v = 13 या 40u + 55v – 13 = 0 (5)
समीकरण 3 और 4 को हल करने पर u = 1/5, v = 1/11
अब u, v के इन मानों को समीकरणों (3) में रखने पर, हम पाते हैं:
1/(x – y) = 1/5
और 1/(x + y) = 1/11
अर्थात् x – y = 5 और x + y = 11 (6)
x और y के सापेक्ष समीकरण को हल करने पर
x = 8, y = 3
उत्तर के सत्यापन्न के लिए x और y के मान समीकरण 1 और 2 में रखकर जांच कर सकते हैं।
समान्तर रेखाएं
समानांतर रेखाएँ किसी समतल में बनी ऐसी रेखाएँ होती हैं जो कभी नहीं मिलती। यह तभी सम्भव है जब इन रेखाओं के बीच की दूरी (अंतर) एक समान ही रहता है, यानि कभी नहीं बदलता।
उदाहरण के लिए रेखाएं a₁ x + b₁ y + c₁ = 0 और a₂ x + b₂ y + c₂ = 0 समान्तर होगीं यदि a₁/a₂ = b₁/b₂ ≠ c₁/c₂
प्रतिच्छेदी रेखाएँ
किसी एक तल की दो भिन्न रेखाएँ, जिनमें एक बिंदु उभयनिष्ठ हो, प्रतिच्छेदी रेखाएँ कहलाती हैं; तथा उभयनिष्ठ बिंदु को प्रतिच्छेद बिंदु कहते हैं।
उदाहरण के लिए रेखाएं a₁ x + b₁ y + c₁ = 0 और a₂ x + b₂ y + c₂ = 0 प्रतिच्छेदी होगीं यदि a₁/a₂ ≠ b₁/b₂
संपाती रेखाएं
जब एक ही रेखा पर अन्य एक या एक से अधिक रेखाएं होती है, तो वह संपाती रेखाएं कहलाती है।
उदाहरण के लिए रेखाएं a₁ x + b₁ y + c₁ = 0 और a₂ x + b₂ y + c₂ = 0 सम्पाती होगीं यदि a₁/a₂ = b₁/b₂ = c₁/c₂
उदाहरण
एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा होना है। यदि पंक्ति में 3 विद्यार्थी अधिक होते, तो 1 पंक्ति कम होती। यदि पंक्ति में 3 विद्यार्थी कम होते, तो 2 पंक्तियाँ अधिक बनतीं। कक्षा में विद्यार्थियों की संख्या ज्ञात कीजिए।
हल
माना एक पंक्ति में विद्यार्थियों कि संख्या x है और पंक्तियों की संख्या y है।
तो कुल विद्यार्थियों की संख्या = x × y = xy
उदाहरण
प्रथम स्थिति के अनुसार अगर एक पंक्ति में 3 विद्यार्थी अधिक होते, तो 1 पंक्ति कम होती।
अर्थात् एक पंक्ति में विद्यार्थियों संख्या = x + 3
तो पंक्तियों की संख्या = y – 1
विद्यार्थियों की कुल संख्या (x + 3) (y – 1) = xy
या x = 3y – 3 (1)
द्वितीय स्थिति के अनुसार अगर एक पंक्ति में 3 विद्यार्थी कम होते, तो 2 पंक्तियां बढ़ जाती हैं।
अर्थात् एक पंक्ति में विद्यार्थियों संख्या = x – 3
तो पंक्तियों की संख्या = y + 2
विद्यार्थियों की कुल संख्या (x – 3) (y + 1) = xy
या 2x = 3y + 6 (2)
समीकरण 1 और 2 को हाल करने पर
x = 9 और y = 4 प्राप्त होते हैं।
अतः कुल विद्यार्थियों की संख्या = xy
= 9 × 4 = 36
यदि समीकरण निकाय a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 a1x + b1y + c1 = 0, a2 x + b2y + c2 = 0 हो तो संगत चरों के गुणांकों का अनुपात देखने पर निम्न स्थिति के अनुसार निर्णय किया जाता है।
We hope that class 10 Math Chapter 3 दो चर वाले रैखिक समीकरण युग्म (Pair of Linear Equations in Two Variables) Notes in Hindi helped you. If you have any queries about class 10 Math Chapter 3 दो चर वाले रैखिक समीकरण युग्म (Pair of Linear Equations in Two Variables) Notes in Hindi or about any other Notes of class 10 Math in Hindi, so you can comment below. We will reach you as soon as possible…